Introducción
En Costa Rica hay varios lugares donde se puede consultar diferentes datos sobre la geografía nacional. Los más visitados posiblemente sean
el Atlas Digital (Ortiz, 2008)
el Proyecto PRIAS(CeNat)
el Sistema Nacional de Información Territorial (SNIT).
Sin embargo, ninguna de estas fuentes muestran los datos en tres dimensiones.
El proyecto iReal 3.0 consiste en la visualización de los hipocentros de los terremotos ocurridos en los últimos veinte años y en la animación de los movimientos de la península de Nicoya producidos por el terremoto del 5 de septiembre del 2012.
En ambos casos se necesita un visualizador en tres dimensiones georreferenciado, que permita mostrar los datos en su posición real y explorarlos con detalle.
Esta necesidad nos llevó a la programación de esta herramienta, que más tarde nos servirá para relacionar con estos proyectos y otros tipos de datos, como por ejemplo, dirección y velocidad de los vientos, precipitaciones, clima, etc.
Del dominio
Como se dijo en Costa Rica hay varias fuentes de datos geográficos. En nuestro caso, se recurrió al proyecto PRIAS(CeNat), que tiene magníficas fuentes de este tipo de datos, y al Atlas Geográfico realizado por el Instituto Tecnológico de Costa Rica (Ortiz, 2008).
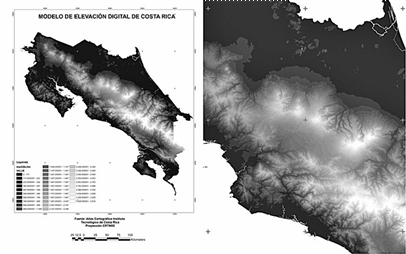
Los datos venían en formatos de dBASE (.dbf) y en modelos de elevación en forma de imágenes del tipo que se muestra en la Figura 1.
Con esta información a la mano, se procedió a generar pruebas de eficiencia en el manejo de este tipo de datos. La primer opción fue trabajar con Javascript (Hernández-Castro & Monge-Fallas, 2017), y como se menciona en el artículo citado se determinó usar el enfoque de requestAnimationFrame( ) de Javascript con la biblioteca Three.js corriendo en Apple Safari® para obtener los mejores resultados.
Posteriormente se programaron prototipos similares, tanto en JavaScript/Three.js como en Java/Processing y Apple Swift®, con la misma idea de seleccionar la plataforma que se desempeñara mejor en el manejo de datos en espacios 3D.
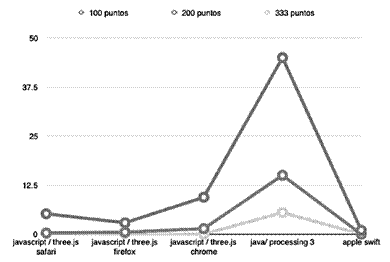
En la Figura 2 se muestran los resultados de las pruebas.
Como se observa JAVA, específicamente Processing 3 con el motor interno de OpenGL (P3D) obtuvo un rendimiento muy superior a todas las demás plataformas. Con esto claro, se procedió a realizar la implementación en este ambiente.
Estado del arte
Se ha escrito mucho desde el artículo clásico del Kenneth G. D Geographic Network Displays (Cox, Eick & He, 1996), hasta trabajos como los de SABINA (Wilhelm, Mailhiot, Arany, Chardine, Robertson, & Ryan, 2015), del año pasado, con mejores técnicas en el manejo de la data para visualizaciones en tres dimensiones.
Existen algunas referencias de enfoques y algoritmos para tratamiento de data relacionada con modelación en 3D, como el caso de Mei-Po Kwan (Kwan, 2000), y de Gallerini (Gallerini & Donatis, 2007); sin embargo, poco se ha trabajado en la visualización de estos ambientes.
También encontramos algunos sistemas propietarios como el Scroops3D (Reid, Christian, Brien & Henderson, 2015), que tiene buenas prestaciones pero, por supuesto, son herramientas costosas.
Un enfoque que sí ha trabajado en los aspectos de visualización y eficiencia es el modelado 3D para juegos por computadora, como ejemplo los casos de Ruzinoor Che Mat (Mat, Shariff, Zulkifli, Rahim & Mahayudin, 2014) y Dieter Frtisch ( Fritsch & Kada, 2004). En estos trabajos se evidencia una tendencia hacia el uso de las tecnologías de gaming para modelar datos geográficos aprovechando la tecnología de alta eficiencia que esta industria necesita.
En nuestro caso, seguimos precisamente esta tendencia, con ambientes como Three.js y Java/ processing, que fueron diseñados más para generación de animaciones y juegos que para herramientas de visualización.
La aplicación
Navegación
El primer problema en que se trabajó fue el conocido como “perdidos en el hiperespacio” (Theng, 1999). Para corregir este aspecto usamos un enfoque ya probado por nuestro grupo (Hernández-Castro, Mata-Montero &Monge-Fallas, 2009), que consiste en limitar la navegación del usuario a dos tipos de giros. Esta estrategia permite que el usuario no se pierda “volando” por el ambiente, sin que se sienta limitado por la herramienta.
El problema conocido como “perdidos en el hiperespacio” radica en la complejidad de navegar en un espacio que tienen tres dimensiones y, por tanto, también tres ejes de giro. Así, en un sistema de “vuelo” normal, se conocen los giros alabeo, dirección o guiñado y cabeceo; los tres giros juntos definen el nuevo vector de dirección sobre el cual se instala “nuevo sistema coordenado” . En otras palabras, un usuario normal puede girar en los tres ejes y definir en qué dirección desea avanzar, esta idea se conoce como el “vuelo de helicóptero” (Fairchild, Poltrock & Furnas, 1999) .
Nuestra solución al problema también pasó por limitar los movimientos del usuario pero de otro modo. “Partiendo de que siempre existe un centro de interés, se limita la navegación del usuario a la superficie de una esfera cuyo centro se ubica en este punto de interés.”(Hernández-Castro, Mata-Montero & Monge-Fallas, 2009).
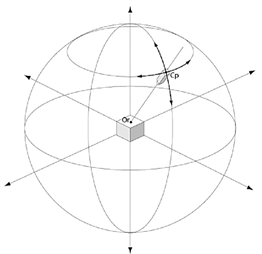
La cámara gira en dos circunferencias; la circunferencia vertical, que siempre es del mismo diámetro, y la circunferencia horizontal, que varía de diámetro según su “latitud” en la esfera (Figura 3). Todo el sistema puede hacerse más pequeño o más grande dando la sensación de zoom in y zoom out. De este modo, la navegación resulta más fluida y sin la sensación de estar limitada.
Triangulación
En el caso de la triangulación, y para mejorar la eficiencia en cuanto a la manipulación de la geografía, se modificaron los datos de tal modo que se pudiera etiquetar qué parte de la matriz cuadrada correspondía a áreas en el mar. La idea era solo mostrar en esta implementación las áreas correspondientes a tierra firme y con esto reducir al menos a la mitad la cantidad de datos visualizados al mismo tiempo.
La secuencia de triangulación también debía ser la misma en todos los polígonos, de modo que las normales de los triángulos tuvieran todas la misma dirección y así el visualizador OpenGL las renderizara del mismo lado.
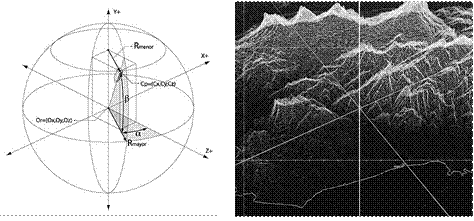
En la Figura 4 se muestra cómo se planificó esta triangulación y la diferencia entre áreas en el océano y en tierra firme. En este caso, si un triángulo tiene un punto “gris” (en el mar) se desiste de renderizarlo. Más abajo se ve el resultado del algoritmo.
Resultados
Zoom
Con la estrategia de la esfera de navegación se hace fácil hacer acercamientos, rotaciones y giros desde cualquier punto, para esto se cambian los tamaños de los diámetros sobre los que gira la cámara en forma proporcional:
Cx = Rmenor * cos (α) + Ox
CY = Rmayor * sin (β) + OY
CZ = Rmenor * sin (α) + OZ
Rmenor = Rmayor * cos (β)
Donde Cx, Cy, Cz son la coordenadas de la cámara.
Ox, Oy, Oz son las coordenadas del punto que se desea observar α es el giro sobre el eje Y y β sobre el eje X; Rmenor el radio del círculo de giro horizontal y Rmayor el radio del círculo de giro vertical (ver detalle en Figura 5).
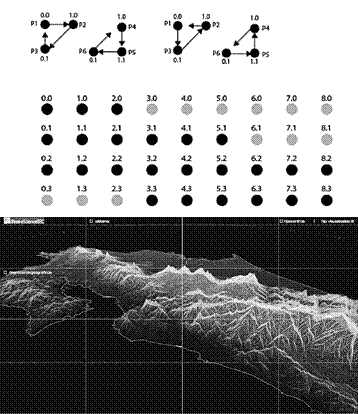
Figura 4 Estrategia de triangulación usada y su resultado al eliminar los puntos correspondientes al océano
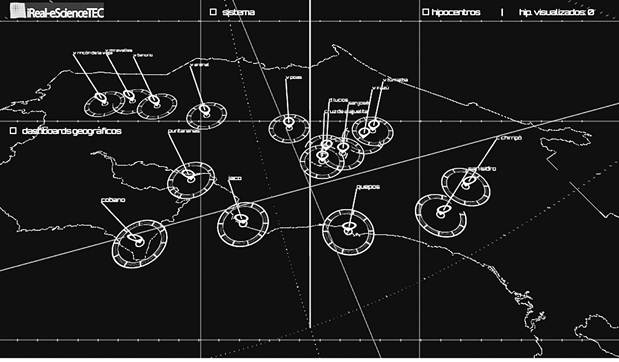
Lugares de referencia
También es posible visualizar lugares de referencia (Figura 6), los cuales se pueden alimentar con un simple archivo “csv”, donde se adjuntan, además del nombre del lugar, sus coordenadas en latitud y longitud. De este modo todo el sistema se visualiza con relación a las latitudes y longitudes de Costa Rica.
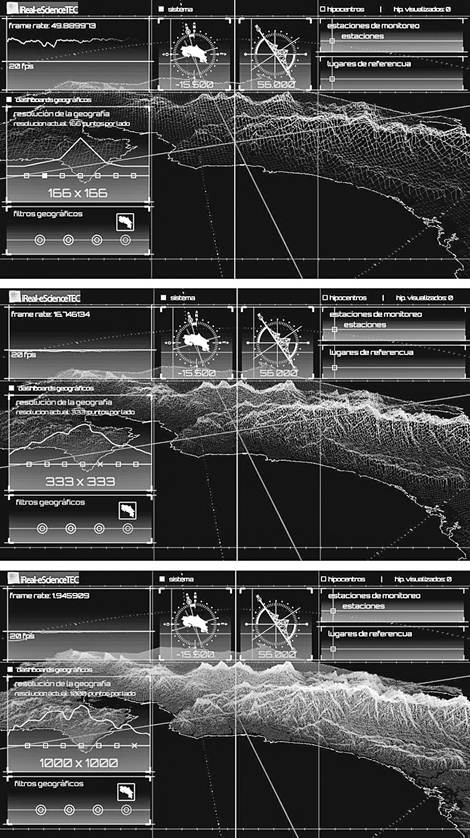
Resoluciones y eficiencia
Debido a que el sistema debe ser escalable y a que los datos fácilmente llevan al procesador (y su tarjeta gráfica) al máximo de sus capacidades, incluye un dashboard (Figura 7) para mostrar la cantidad de frames per seconds (ftp) en cada momento. Además, es posible cambiar la cantidad de puntos desplegados, o resolución en que se despliega la geografía, para poder ajustarla a la capacidad del equipo en cada momento.
Conclusiones y trabajo futuro
El sistema fue implementado de modo escalable y georreferenciado, para visualizar otros datos en función de su longitud y latitud, sin necesidad de hacerle ningún cambio. Es una plataforma estable para continuar con los proyectos siguientes, que son la visualización de los hipocentros de terremotos en dos décadas y del movimiento de la península de Nicoya producido por el terremoto de septiembre del 2012.
Para el futuro, se debe continuar tratando de incrementar la eficiencia. En este momento, con una computadora personal, solo es posible visualizar hasta un millón de puntos a la vez. Para algunas aplicaciones esto puede resultar poco. Con el fin de lograrlo, se pretende hacer pruebas en C++, que en aplicaciones preliminares ha mostrado un mejor desempeño. La otra posibilidad es implementar una versión del sistema en la nueva máquina de juegos de Apple, “METAL”, que promete ser más rápida porque se salta la capa de OpenGL y trabaja directamente con el procesador gráfico.
Este modelo, además, servirá en el futuro para visualizar otra data, como velocidades y direcciones de vientos, precipitaciones y datos meteorológicos.