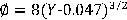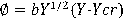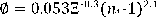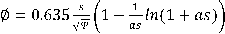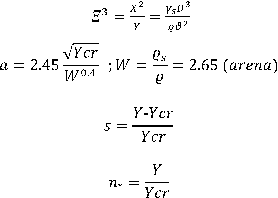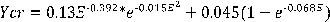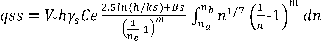Introducción
Es bien conocido que el equilibrio de una partícula en el lecho de un río está gobernado por el balance entre las fuerzas desestabilizadoras de sustentación y de arrastre, y las fuerzas estabilizantes de gravedad y de entrabamiento de las partículas (Aguirre-Pe, 2000). El transporte de sedimentos de las partículas de la cama por el flujo de agua, puede estar en forma de carga de fondo y carga suspendida, dependiendo del tamaño de las partículas de material de cama y las condiciones de flujo. (Van Rijn, 1993)
El transporte de sedimentos total para un río está dado por dos partes: la primera por los sedimentos que son transportados en el fondo del cauce o en la cama del río, denominados por las letras “qsb”; la segunda por los sedimentos que son transportados en suspensión, denominados por las letras “qss”. La suma de estos dos parámetros da como resultado el transporte total de los sedimentos que son llevados por el río, denominado por las letras “qs”. Este resultado puede ser expresado en términos volumétricos, metros cúbicos entre metro por segundo [m3/m*s] y en términos gravimétricos, newton entre metro por segundo [N/m*s].
La complejidad de la mecánica del transporte de sedimentos es tal que no ha podido proponerse una verdadera ecuación dinámica del transporte de la fase sólida de un flujo de agua y sólidos. En su lugar han florecido en distintas partes del mundo ecuaciones empíricas, semi empíricas o basadas en distintas teorías que dan razón de ciertas observaciones. Estas ecuaciones son aproximadas, no exactas, solo válidas dentro del rango de valores para el que fueron obtenidas. (Martín, 2002).
Para calcular el transporte de sedimentos que ocurre en el fondo del cauce así como el que ocurre en suspensión, hay varias ecuaciones propuestas por diferentes autores. Como lo mencionan García & Sala, (1985), la mayoría de las fórmulas se han desarrollado a partir de estudios realizados en canales experimentales, con los que se ha intentado obtener una relación entre el transporte de fondo y las condiciones hidráulicas del flujo o la sedimentación.
Algunas de las ecuaciones más conocidas, las cuales se usaron para realizar los cálculos del transporte de sedimentos del fondo del cauce, son las propuestas por Yalin, Bagnold, Van Rijn, Meyer-Peter & Müller. Los resultados al obtenidos por medio de las ecuaciones anteriores se graficaron. Estos gráficos son de suma importancia ya que dan una idea del tipo y la cantidad de sedimentos, que en diferentes condiciones el río, puede transportar.
El principal objetivo del estudio fue estimar la capacidad hidráulica que tiene el río La Estrella para transportar sedimentos, tanto a nivel del fondo del cauce como sedimentos en suspensión. La razón de ellos es que este río ha traído muchos problemas debido a sus desbordamientos, como grandes pérdidas para las plantaciones que se encuentran alrededor de este y a la población que vive cerca, se espera comprender un poco más su comportamiento y poder evitar algunos desastres.
Metodología
Descripción de la cuenca
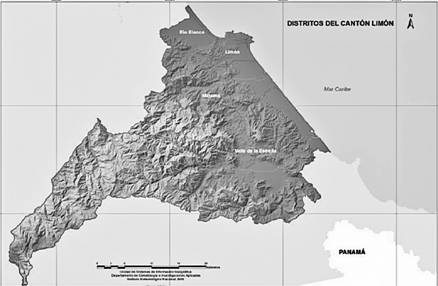
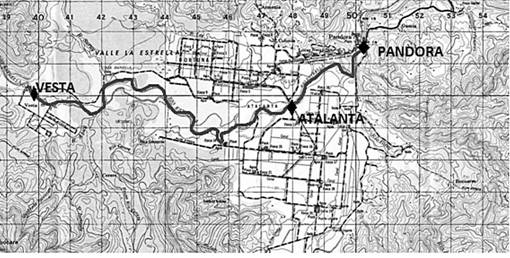
El río en estudio se encuentra en la provincia de Limón, zona del Caribe, específicamente en el valle de La Estrella, el cual se puede apreciar en la Figura 1. La cuenca del río La Estrella tiene una extensión aproximada de 1031km2 lo que representa un 2,02% de la superficie nacional (Rojas, 2011). La sección en estudio, que abarca desde Vesta hasta Pandora, tiene una longitud de 14 kilómetros y atraviesa una finca bananera; esta se inunda a causa del río.
En esta cuenca el rasgo climático típico es el régimen de precipitación del Caribe, el cual en Costa Rica se caracteriza por presentar una estación lluviosa a lo largo de casi todo el año, con disminución de las lluvias en los meses de setiembre y octubre en particular en esta cuenca (Rojas, 2011).
Toma de muestras
Se realizaron una serie de aforos mensuales del río La Estrella y de sus principales afluentes. Para estos aforos se utilizaron dos correntómetros, Universal Current Meter F1 y Mini Current Meter M1. Se escogieron tres puntos de muestreo en el cauce principal: Vesta, Atalanta y Pandora; se muestrearon seis afluentes: Suruy, Abuy, Cerere, Niñey, Bitey, Duruy y Ley. También se tomaron diferentes muestras del material que contenía el fondo del cauce, en cada visita, para obtener información de los sedimentos presentes en cada punto. Los resultados que se presentan en este artículo pertenecen a los tres puntos de medición del cauce principal, Vesta, Atalanta y Pandora, en orden de mayor altitud a menor altitud respectivamente; estos puntos de medición se pueden observar en la Figura 2.
Procesamiento de la información
Con los datos obtenidos de los aforos realizados se obtuvo el caudal en cada punto, también se obtuvo el perfil transversal de cada sección en donde se efectuaron las medidas. Las muestras del material tomado se procesaron en el Laboratorio de Suelos de la Escuela de Ingeniería Agrícola, donde se tamizaron y los resultados se graficaron para observar la curva de distribución de los diámetros de los granos. Analizando estas curvas y tomando en cuenta las diferentes condiciones para los distintos puntos, se aplicaron las diferentes ecuaciones para obtener los resultados del transporte de sedimentos.
Para la realización de los cálculos se utilizaron los caudales que fueron medidos en los distintos puntos, los diámetros de los sedimentos y las alturas del agua o profundidades. Para la elección de los diferentes diámetros, se utilizó un promedio de los rangos que se encontraron en las tablas de clasificación de sedimentos, de acuerdo con su diámetro. Luego en las curvas de distribución que se elaboraron para cada punto de muestreo, se observó qué diámetros se presentaban en cada sitio de medición, para utilizar diámetros de sedimentos que estuvieran presentes.
Los cálculos se realizaron en dos etapas: la primera fue referida al transporte de sedimentos en el fondo del cauce y la segunda al movimiento de sedimentos en suspensión o flotación. Cabe resaltar que se usó la pendiente del tramo de Pandora a la desembocadura para todos los cálculos.
Ecuaciones utilizadas
Por medio de las ecuaciones o fórmulas de transporte de fondo, se cuantifica el caudal sólido de una corriente en función de sus características hidráulicas y de las características geométricas y granulométricas del cauce (Martín, 2002).
Para calcular la cantidad de sedimentos que son transportados por el río, se utilizaron diferentes ecuaciones de diferentes autores. El cálculo del transporte de sedimentos en el fondo del cauce se realizó por medio de las siguientes ecuaciones, y en un futuro, se puede comparar con mediciones reales de transporte de sedimentos para ver cuál es la ecuación que más se acerca a las condiciones que se presenten en el río.
Meyer-Peter y Müller Formula
Bagnold’s Formula
Van Rijn
Yalin
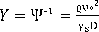 movility number (también llamado el parámetro de Shield)
movility number (también llamado el parámetro de Shield)
Y cr = valor de Y en la iniciación de la etapa crítica del transporte de sedimentos b= valor gráfico (Ver Yalin 1972)
En lo anterior, υ* es la velocidad de corte (= (gSh)1/2). Además, ρ es la densidad del fluido, ν es la viscosidad cinemática del fluido, ρs es la densidad de grano y γs el peso específico del material del lecho sumergido. En este trabajo, estos fueron identificados con 1000 kg/ m3, 6,10 m2/s, 2,650 kg/m3 y 16,186.5 N/m3, respectivamente; mientras Ycr se determinó a partir de la siguiente ecuación, debida a Yalin y da Silva (2001):
Cuando el valor de la velocidad cortante excede la velocidad de caída de las partículas, las partículas pueden ser levantados a un nivel donde las fuerzas de turbulencia pueden ser iguales o mayores al peso de la partícula y como resultado el movimiento de la partícula en suspensión es ocasional y aleatoria. La velocidad de las partículas es muy parecida a la velocidad del fluido (Van Rijn, 1993).
Para realizar el cálculo del transporte de sedimentos en suspensión se utilizó la siguiente ecuación:
h= profundidad del agua
C ∈ = concentración adimensional en el nivel ε, en el que ε es el espesor de la capa de la cama del cauce k s = 2D 50 rugosidad del material de la cama del cauce B s = función de la rugosidad η = z/h, en donde z es el eje vertical, con origen en la cama del cauce
En este trabajo, la rugosidad de la función Bs fue evaluada por medio de la siguiente ecuación, dada por Yalin y da Silva (2001):
donde Re* es el número de la rugosidad de Reynolds 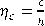 , mientras ε es calculado como 2DY/Ycr.
, mientras ε es calculado como 2DY/Ycr.
Resultados y discusión
Los gráficos se realizaron a la misma escala, con el propósito de observar de una manera más clara la diferencia entre los resultados de lo que se calculó.
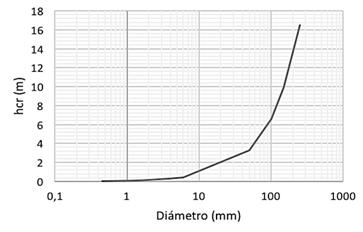
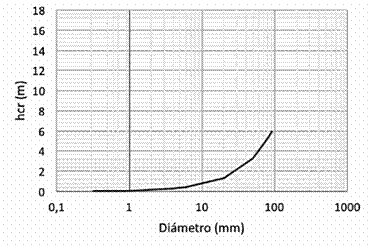
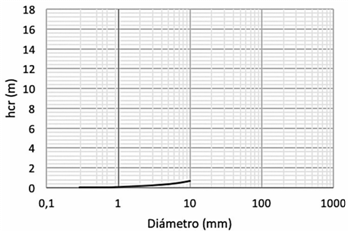
Al calcular el movimiento de sedimentos en el fondo del cauce, es importante saber qué altura de agua es requerida para que dé inicio el movimiento de los sedimentos de diferentes diámetros. En las figuras 3, 4 y 5 se observa la altura necesaria o la altura crítica de agua para iniciar el movimiento de sedimentos de diferentes diámetros en los puntos de muestreo localizados en Vesta, Atalanta y Pandora, respectivamente.
Se puede observar que en el punto localizado en Vesta, Figura 3, es necesaria una altura de agua mucho mayor que en los otros dos puntos, los cuales se encuentran a una altura sobre el nivel del mar menor. En Vesta se encuentran sedimentos de diámetros mucho más grandes que en los otros puntos, porque este es el punto de mayor altitud de la zona en estudio y el más cercano a la zona montañosa. Por ejemplo, en Vesta, para mover una piedra de un diámetro de 100 mm se requiere una altura de 6,6 m, y para lograr que se mueva todo el material del fondo del cauce se requiere una altura de 16,5 m.
Los cálculos utilizados para obtener las tres curvas fueron los mismos para todos los puntos. La diferencia entre las tres curvas es su longitud, que está en función del material de mayor diámetro en cada punto.
Los resultados obtenidos se compararon con las condiciones presentes en el lugar de estudio en las distintas giras realizadas. Con los datos de las curvas anteriores, se corroboró lo que se observó en campo, es decir que en las condiciones presentes en el sitio, diámetros relativamente grandes no se movían.
Al tener una idea bastante clara del tamaño del material que el río logra mover, se procedió a realizar los cálculos del transporte de sedimentos [qsb] = [m3/m*s], para lo cual se aplicaron las diferentes ecuaciones de los diferentes autores ya mencionados, con el fin de comparar los distintos resultados. Al comparar los resultados se pudo obtener un rango de la cantidad de sedimentos que estaban siendo transportados.
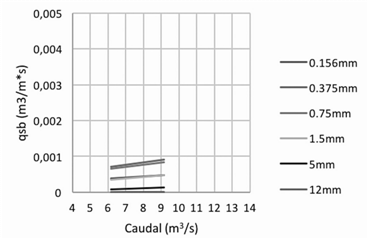
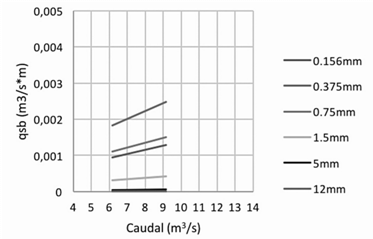
En los gráficos siguientes se presentan los resultados de transporte de sedimentos del fondo del cauce en los tres puntos seleccionados sobre el cauce principal.
En ellos se muestran las cantidades de sedimento que cada caudal puede transportar, según el diámetro de partícula, y para los diferentes diámetros escogidos. Se utilizaron los datos de los caudales medidos en las diferentes visitas al campo.
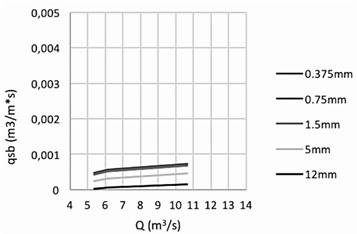
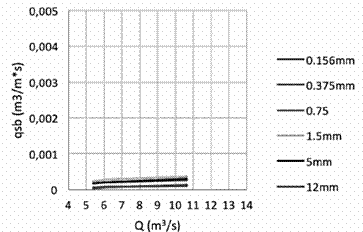
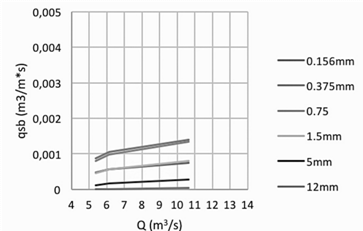
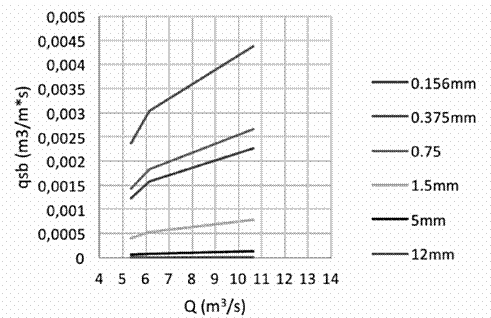
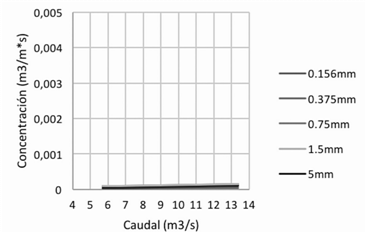
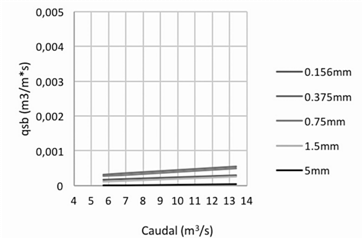
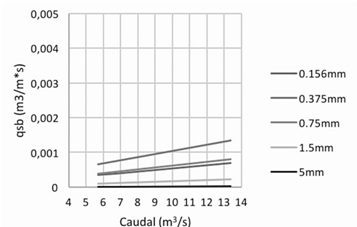
Se observa en los siguientes gráficos que los valores del transporte de sedimentos en la locación de Vesta calculados por las distintas fórmulas son diferentes. Los valores máximos se presentan cuando se aplica la ecuación de Van Rijn, Figura 9, y los mínimos cuando se aplica la ecuación de Bagnold, Figura 7. No se puede decir que alguno de estos resultados es erróneo, ya que no se cuenta con valores reales del movimiento que se da en este punto, para establecer la comparación entre ambos; sin embargo, los resultados obtenidos por medio de las diferentes ecuaciones permiten contar con un rango de valores para hacer las aproximaciones con la realidad.
En relación con las mediciones hechas en el punto de Atalanta, se puede observar que tres de las cuatro ecuaciones aplicadas dan valores muy similares. Nuevamente con la ecuación de Van Rijn, Figura 13, se obtienen los valores máximos. De igual manera que en el caso anterior no se puede concluir cuál es la ecuación que más se asemeja a las condiciones del río ya que no se cuenta con mediciones reales.
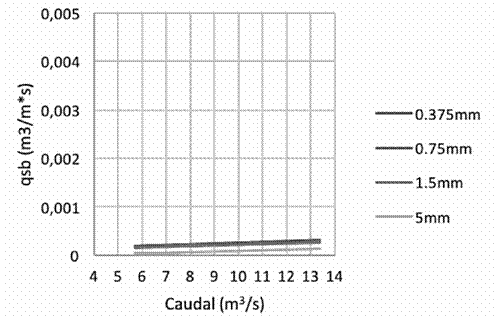
Figura 10 Cantidad de sedimentos de fondo en Atalanta, utilizando la ecuación de Meyer-Peter y Müller
Para el caso del punto más bajo del cauce, en Pandora, se observa que los resultados obtenidos por medio de las diferentes ecuaciones difieren un poco entre ellos; pero al igual que en los dos casos anteriores, los valores máximos se presentan con la ecuación de Van Rijn, Figura 16, y los mínimos con la ecuación de Bagnold, Figura 15.
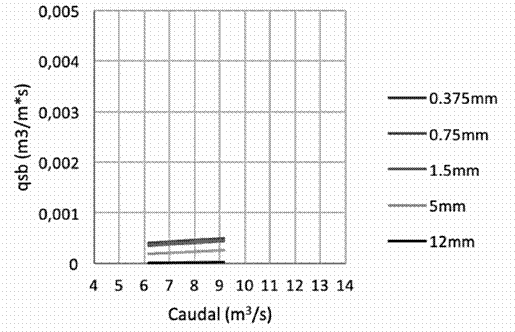
Figura 14 Cantidad de sedimentos de fondo en Pandora, utilizando la ecuación de Meyer-Peter y Müller
A partir de los resultados presentados se puede observar que el movimiento de sedimentos es mayor en Vesta. Esto debido a que este punto presenta gran cantidad de sedimentos de todo tamaño, además de que allí las profundidades son mayores que en los otros puntos del cauce principal, lo que provoca que más sedimentos sean puestos en movimiento, como se explicó anteriormente en relación con el cálculo de la altura crítica (hcr).
En contraste, el transporte de sedimentos es menor en Atalanta que en los otros dos puntos de medición, esto se debe a que las secciones transversales en Vesta y en Pandora son mucho más angostas que en Atalanta, por lo cual las profundidades en estos dos puntos son mayores, a lo que se suman velocidades mayores, de modo que las probabilidades de que se presente transporte o movimiento de sedimentos de diámetros grandes también es mayor.
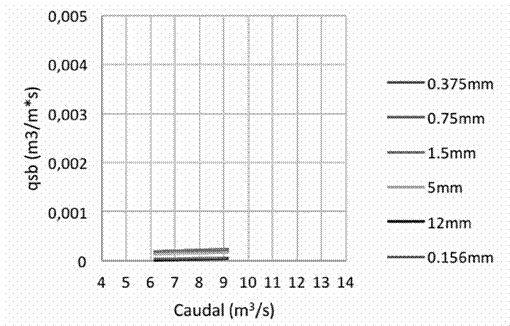
En cuanto al transporte de sedimentos en suspensión, se calculó para los tres puntos de medición sobre el cauce principal. Como se puede observar solo se realizaron cálculos para sedimentos de dos diámetros diferentes, esto debido a que los sedimentos en suspensión que lleva el río son de diámetros muy pequeños, siendo los de 0,156mm y 0,375mm los más representativos en las condiciones halladas en los tres lugares.
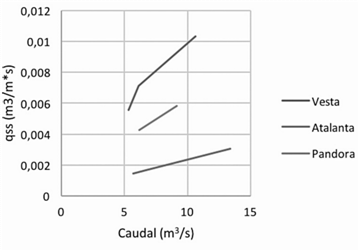
Figura 18 Cantidad de sedimentos en suspensión de diámetro 0,156 mm, utilizando la ecuación de Van Rijn
Figura 19 Cantidad de sedimentos en suspensión de diámetro 0.375mm utilizando la ecuación de Van Rijn
Las cantidades de sedimentos de los dos diámetros representativos se pueden observar en las figuras 18 y 19. Entre más pequeño sea el diámetro más fácil es para el río transportarlo y conforme el diámetro va aumentando, la cantidad que se puede transportar en suspensión disminuye, bajo las mismas condiciones. Si se compara los resultados del transporte de los sedimentos de 0,156 mm de diámetro, Figura 18, con los de sedimentos de 0,375 mm de diámetro, Figura 19, se puede observar una gran diferencia entre las cantidades transportadas en suspensión.
Conclusiones
Se logró cuantificar los sedimentos de fondo y en suspensión del río La Estrella. Los resultados mostraron que el transporte de sedimentos es muy bajo, hecho que tiene relación con las condiciones que se pudieron observar en campo, ya que durante la época de muestreo no se presentaron muchas precipitaciones y, en consecuencia, los caudales eran muy pequeños, de modo que la capacidad hidráulica del río para transportar diferentes tamaños de sedimentos era reducida.
Se comprobó que para mover material con partículas de diámetros muy grandes se requieren alturas de agua considerables; esto se determinó para el punto de muestreo localizado en Vesta. De igual manera, se encontró que la cantidad de sedimentos transportados en suspensión, que son de diámetros muy pequeños, aumenta con la presencia de caudales muy grandes.
Se logró una caracterización de la capacidad hidráulica del río La Estrella en un año de bajas precipitaciones y bajos caudales.
Los resultados obtenidos permitirán hacer futuros modelos para comprender un poco más el comportamiento del río y en qué puntos son depositados los diferentes sedimentos. Con los resultados de ello, se podrá determinar qué zonas son más propensas a desastres y diseñar algunas obras de protección, tanto para los campos agrícolas como la infraestructura civil.
Recomendaciones
Son las siguientes:
Tomar las muestras del fondo del cauce con instrumentos apropiados para poder obtener datos más reales del movimiento de los sedimentos y poder correlacionarlos con los resultados teóricos, obtenidos por medio de las distintas ecuaciones.
Realizar más mediciones en distintas épocas del año para obtener valores del transporte de sedimentos bajo diferentes condiciones y predecir el comportamiento del río a lo largo de todo el año.
En este caso, el río presenta material mixto debido a que se presentan diferencias significativas entre los sedimentos en los puntos de medición. En la actualidad nuevas investigaciones o teorías afirman que el material de diámetros más pequeños se esconde entre las rocas de mayor tamaño, por lo cual los resultados obtenidos podrían variar un poco.