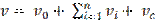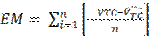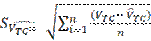Introdução
O manejo florestal consiste em administrar a obtenção de benefícios econômicos, sociais e ambientais, respeitando-se os mecanismos de sustentabilidade do ecossistema. O Brasil ocupa uma área de 8.514.876 Km², sendo que 5.217.423 km², ou seja, corresponde a 61% do território brasileiro estão dentro da Amazônia Legal (1). Está inserido nos quatro ecossistemas: cerrado, pantanal, floresta amazônica e área de transição, objeto do manejo e considerando-se cumulativa ou alternativamente, a utilização de múltiplos produtos e subprodutos madeireiros e não madeireiros, bem como a utilização de outros bens e serviços de natureza florestal consta do Art. 25, parágrafo único do decreto 8.188/2006. (2).
Estes sistemas utilizam as melhores técnicas de exploração disponíveis, visando reduzir os danos da floresta, o desgaste do solo, erosão, além de proteger as bacias hidrográficas, atenuar o risco de incêndios e permitem a manutenção da regeneração natural e proteção da diversidade biológica.
O potencial econômico madeireiro das espécies é mensurado a partir de estimadores volumétricos. A estimativa do volume de madeira de florestas nativas normalmente é realizada por meio de inventário florestal, utilizando-se um conjunto de dados como base para se realizar inferências sobre as variáveis de altura, volume e número de árvores por hectare (3).
A regressão pode ser amplamente utilizada nas estimativas e prognoses da produção madeireira, constituindo um procedimento eficiente (4), (5). Para a estimativa do volume de árvores, é comum o emprego de modelos de regressão com as expectativas de altura (6). Porém, recentemente, vem sendo estudada a utilização de Redes Neurais Artificiais (RNA) para a estimação dessas variáveis, e foram encontrados resultados satisfatórios de sua aplicação, muitas vezes até superiores (7).
O uso de ferramentas de inteligência artificial na modelagem de crescimento e produção ainda é um assunto novo e pouco explorado no Brasil. Em Ciência Florestal, diversos tópicos podem ser potencialmente tratados por RNAs, entre eles a modelagem do volume de árvores, relações hipsométricas e equações de taper, obtendo resultados expressivos (8), (9), (10). As RNAs, por outro lado, são aproximadores universais que aprendem com os dados, considerando que os dados falam por si e, têm apresentado excelentes resultados na solução de problemas nas mais diversas áreas do conhecimento humano, principalmente na solução de problemas em ambientes mapeados por variáveis de domínios imprecisos, como no caso do problema da determinação do volume comercial de espécies florestais (11) (12).
Diante do exposto, esta pesquisa tem como objetivo estimar o volume de madeira de espécies nativas provenientes de PMF com o uso de redes neurais artificiais comparando com método de regressão linear na estimativa de volume.
Material e métodos
O estudo foi realiza na unidade de Manejo Florestal, na fazenda Uberlândia-PA, localizada na Gleba Joana Perez I, entre os municípios de Bagre, Portel, Baião e Oeiras no Estado do Pará. Essa Unidade de Manejo Florestal (UMF I) possui uma área de 45.657,5 hectares, e está localizada entre os municípios de Santarém e Juruti, Estado do Pará, onde em 2012 iniciou-se sua produção no mês de junho, sendo manejada uma área de 3.000 hectares, que foi certificada com o selo FSC no dia primeiro de outubro do mesmo ano.
Segundo a classificação de Köppen a região apresenta clima tropical úmido (Amw), caracterizado por apresentar chuvas do tipo monção, isto é, quando apesar de oferecer uma estação seca de pequena duração, possui umidade suficiente para alimentar a floresta tropical. Mantém elevados índices pluviométricos (cerca de 2.400mm de chuva), alta temperatura média do ar (26°C), e umidade relativa superior a 85% (13).
A vegetação do estado do Pará é predominantemente composta pela Floresta Amazônica (floresta tropical pluvial). Em mata de terra firme são encontradas as castanheiras, enquanto em áreas de mata de várzea, encontram-se as seringueiras. Na Ilha do Marajó e nas várzeas de alguns rios são encontrados campos limpos e ao longo do litoral são mangues.
Cubagem Rigorosa
O método utilizado para a cubagem rigorosa foi o de Smalian. Foi realizado o planejamento para a que a coleta de dados abrangesse a variabilidade das espécies, circunferências e alturas das árvores comerciais presentes na área da floresta estudada.
A seleção das árvores para a cubagem foi realizada a partir da distribuição da frequência diamétrica. Foi feita a seleção e a cubagem rigorosa de árvores-amostra abatidas com DAP ≥ 45 cm de forma a contemplar toda a distribuição diamétrica encontrada na área inventariada.
Foram cubadas 864 árvores (pois estas foram autorizadas para exploração) na determinação do volume rigoroso utilizando a metodologia de Smalian, que indica que o volume de cada seção foi somado para obter o volume total das toras de acordo com a equação 1:
Em que: v= volume, vo= volume do toco, vt = volume das secções transversais e vc= volume do cone.
Os dados destas árvores serviram de base para o ajuste dos modelos de volume relacionados na Tabela 1. Os modelos de volume testados foram selecionados na literatura existente sobre o tema, sendo uns dos mais utilizados na área (14).
2Das 864 árvores cubadas, foram selecionadas 120 (divididas entre as diferentes classes de diâmetro) para a validação das equações testadas, permanecendo 744 árvores para montar a matriz de variáveis e encontrar o melhor modelo estatístico.
As 120 árvores usadas para validação foram selecionadas aleatoriamente dentro de todas as classes diamétricas de acordo com a frequência das classes, tendo maior frequência nas primeiras classes diamétricas pelo fato de ser uma área nativa, sendo assim, a seleção ficou distribuída da seguinte forma: De 50 a 59,9 cm: 20 árvores; De 60 a 69,9 cm: 20 árvores; De 70 a 79,9 cm: 20 árvores; De 80 a 89,9 cm: 15 árvores; De 90 a 99,9 cm: 15 árvores; De 100 a 109,9 cm: 15 árvores; De 110 a 119,9 cm: 10 árvores; > 120 cm: 5 árvores.
Modelos de Regressão e Redes Neurais Artificiais
Os modelos de regressão foram ajustados a partir da análise de correlação entre as variáveis mensuradas na floresta. Já as configurações de RNA testadas variaram em relação ao número de neurônios na camada oculta. Os testes foram realizados utilizando o sistema Neuro 4.0, e as estatísticas analisadas foram: Coeficiente de correlação, Raiz quadrática média do erro (RQME), Soma dos Quadrados Residuais (SQR), variância média e análise gráfica de resíduos.
A estimação do volume comercial de árvores pode ser feita por meio de diversas configurações de RNA, foi utilizado o algoritmo de aprendizagem Resilient Propagation, proposto por (15), como alternativa mais eficiente e recomendada para RNA do tipo Multilayer Perceptron com o número de neurônios ocultos variando entre 01 e 15 (totalizando 300 redes treinadas). A função de ativação foi sigmoide com três mil ciclos como critério de parada. Utilizou-se 70% dos dados para treinamento e 30% para validação, separados de forma aleatória.
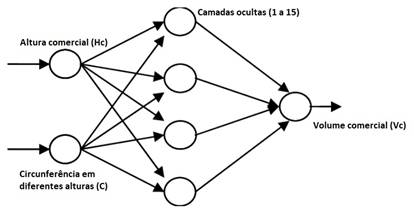
A figura 1 demonstra o esquema utilizado para treinamento das redes neurais, sendo que na camada de entrada estão inseridas 20 variáveis, sendo elas: altura comercial (hc) e a circunferência em 19 diferentes alturas do fuste. Nas camadas ocultas ou intermediárias variaram a quantidade de neurônios em cada uma (de 1 a 15). E na camada de saída temos a variável desejada, o volume comercial (VC).
Figure 1. Tested artificial neural network architecture.
Os critérios escolhidos para comparação entre a técnica de regressão e redes neurais artificiais, na estimativa do volume, foram: Erro médio Absoluto (EM) (equação 2), e erro padrão residual (Syx) (equação 3) e análise gráfica dos resíduos (16). Sendo descritos pelas fórmulas:
Em que: EM= erro médio absoluto; VTC = volume total observado; VTC= volume total estimado; n = número de observações; SVTC erro padrão residual.
Where: EM = absolute mean error; VTC = total observed volume; Vct= estimated total volume; n = number of observations;SVct= residual standard error.
Resultados e discussões
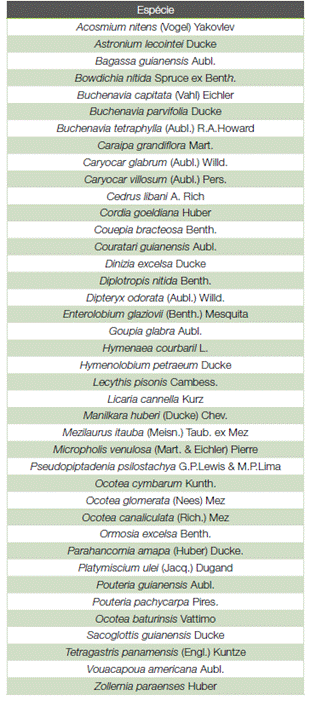
As 864 árvores cubadas correspondem à 40 espécies nativas da região amazônica da região de Portel, no estado do Pará. As espécies foram identificadas e podem ser observadas na tabela 2.
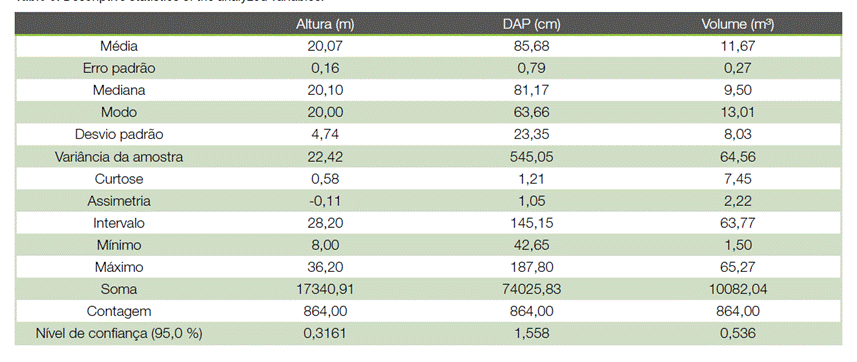
As estatísticas descritivas (Tabela 3) apresentam grande variabilidade, principalmente dos volumes, refletindo uma característica de florestas nativas. A curtose indica curva leptocurtica e a assimetria positiva para DAP e volume e negativa para H comercial indicando que existe um grande número de árvores concentradas nas menores alturas. A dispersão dos dados das variáveis H comercial, DAP e volume são considerados altos (CV%>20), indicando elevada variação que é o esperado para áreas nativas (17).
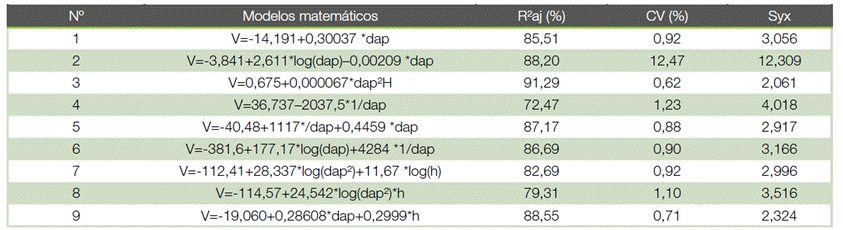
A tabela 4 apresenta os modelos matemáticos ajustados e parâmetros estatísticos utilizados para a escolha do mais adequado.
Como mostrado na tabela 4, o modelo 3 (Spurr) foi o que apresentou melhor ajuste aos dados, com valores de R²aj de 91,29; CV% de 0,62 e Syx de 2,061. Valores semelhantes foram encontrados por (18), que encontraram R²aj de 0,96; CV% de 10,3 e Syx de 9,9; ao ajustarem modelos volumétricos para a espécie Calophyllum brasiliense no sul do Tocantins.
Como critério de parada do algoritmo de treinamento utilizou-se o número total de ciclos igual a 3.000 ou erro médio inferior a 1%, conforme sugerido por (19). Portanto, finalizou-se o treinamento quando um dos critérios foi atingido e a melhor rede para estimar o volume foi selecionada. Para o treinamento das redes neurais artificiais utilizou-se o software Neuro 4.
A figura 2 apresenta os valores de RQME%, variância, SQR e correlação, onde pôde-se notar uma estabilização quando se atinge 12 neurônios na camada intermediária.
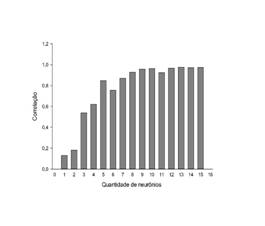


Figura 2 Estatísticas para as diferentes quantidades de neurônios na camada intermediária das redes.
Figure 2. Statistics for the different amounts of neurons in the middle layer of the networks.
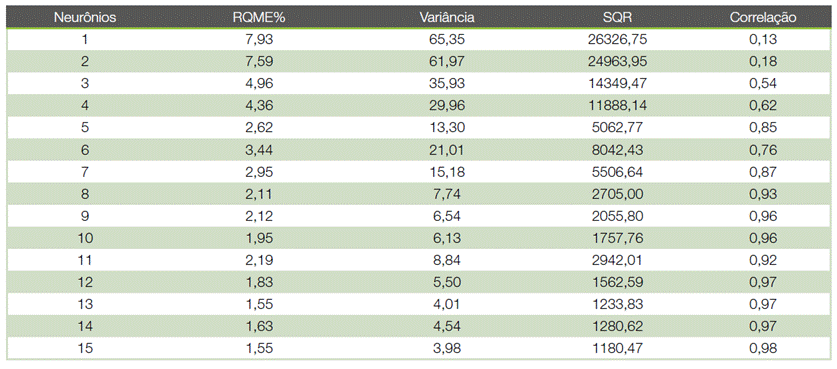
Pelos ensaios realizados com RNAs, foi constatado que a melhor estimação do volume foi obtida utilizando uma RNA multicamada com quinze neurônios na camada intermediária (tabela 5).
Tabela 5 Valores médios encontrados para as 20 redes treinadas para cada quantidade de neurônios na camada intermediária.
Entre as 20 redes treinadas com 15 neurônios na camada intermediária, a rede 299 foi a que apresentou melhores parâmetros para estimativa de volume comercial para as 40 espécies nativas, apresentando a estatística mostrada na tabela 6.
Tabela 6 Parâmetros estatísticos para treinamento e validação da rede 299 com 15 neurônios na camada intermediária para estimativa de volume comercial de 40 espécies nativas na região de Portel - PA.

O erro médio absoluto obtido pela RNA 299 (melhor rede entre as 300 redes testadas), foi de 0,0652; aproximadamente 65% menor quando comparado com o obtido pelo modelo 3 (Spurr) com erro médio absoluto de 0,1853. A RNA 299 ainda apresentou um erro padrão residual (Syx) de 0,2553, valor 39% inferior ao encontrado pelo modelo 3 (0,4304), a correlação encontrada para o modelo 3 (Spurr) foi de 0,963, inferior ao valor encontrado para a rede 299, como mostrado na tabela 5, comprovando com base nas estatísticas de ajuste a sua superioridade em estimar volumes de árvores individuais nesse estudo (20) ao comparar o método de regressão tradicional e redes neurais artificiais para estimar o volume de espécies nativas na Bahia encontrou valores de R²aj igual a 0,879 para o modelo de Spurr, e ao usar redes neurais artificiais encontrou correlação entre 0,88 e 0,99; e RQME entre 10% e 23%.
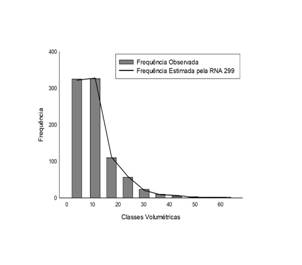
A figura 3 demonstra o histograma de distribuição de classes volumétricas observadas e estimadas pela RNA 299 e modelo 3 (Spurr), onde é possível constatar as boas estimativas de ambos os métodos.
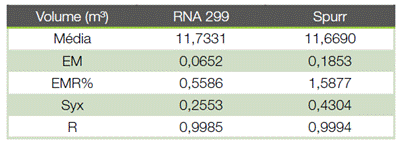
Na tabela 7 podemos comparar os valores do erro médio absoluto, relativo e erro padrão residual.
Pelos ensaios realizados com RNAs, foi constatado que a melhor estimação do volume foi obtida utilizando uma RNA multicamada direta, com quinze neurônios na camada intermediária. O erro médio absoluto obtido pela RNA 299 (melhor rede entre as testadas), foi de 0,0652, aproximadamente 65% menor quando comparado com o obtido pelo modelo de regressão de Spurr com erro médio absoluto de 0,1853. A RNA 299 ainda apresentou um erro padrão residual (Syx) de 0,2553, valor 39% inferior ao encontrado pela regressão de Spurr (0,4304), comprovando com base nas estatísticas de ajuste a sua superioridade em estimar volumes de árvores individuais nesse estudo. A distribuição volumétrica para a equação de Spurr apresentou uma subestimação para a primeira classe volumétrica (7,87 m³) e superestimação na segunda classe (14,25 m³) e terceira classe (20,62 m³).
Figure 3. Histogram of volumetric distribution for RNA 299 and Model 3.
A estimativa das classes volumétricas feita pela RNA 299 foi bastante precisa, como demonstrado na figura 3, não apresentando nenhuma tendência de superou subestimação, já o modelo 3 apresentou uma pequena subestimação na primeira classe e uma superestimação na segunda classe volumétrica.
O valor residual médio para a RNA 299 foi de 0,1174 m³ por árvore, já o modelo 3 obteve um resíduo de 0,2504 m³ por árvore. Assim como no ajuste, a RNA apresentou-se mais eficaz na estimativa do volume, embora os resíduos do modelo 3 se apresentem de forma mais compacta, não apresentando nenhum ponto crítico de tendência no decorrer da distribuição, como mostrado na figura 4. Assim como no ajuste, a equação advinda de redes neurais apresentou-se mais eficaz na estimativa do volume, embora os resíduos do modelo estatístico apresentar resíduos melhor distribuídos e de forma mais compacta, não apresentando nenhum ponto crítico de tendência no decorrer de toda a linha de regressão. Por vez, a equação de regressão melhorou sua distribuição residual quando comparada com os resíduos do ajuste, no entanto, resultados estatísticos inferiores a RNA se mantêm. A avaliação da distribuição é importante para que o processo de estimação mantenha a mesma distribuição dos dados observados, evitando-se, assim, distorções e alterações no comportamento da variável original.
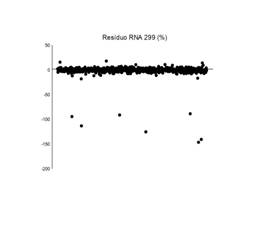
Figura 4 Análise gráfica de resíduos da modelagem volumétrica determinada pelas redes neurais artificiais e modelo de regressão.
Figure 4. Graphical analysis of residuals from volumetric modeling determined by artificial neural networks and regression model.
A análise gráfica e estatística utilizada mostrou que todos os modelos apresentaram resultados sem tendenciosidade e livre de bias.
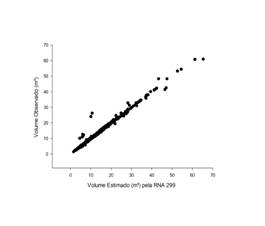
A figura 5 apresenta o gráfico de regressão entre os valores observados e estimados pela RNA 299 e o modelo 3, mostrando a boa qualidade de ajuste dos dois métodos propostos, e evidenciando a superioridade de ajuste das redes neurais artificiais.
As técnicas de inteligência artificial apresentaram coeficientes de correlação superior ao modelo de Spurr, contudo tal diferença não se apresenta significativa para os dados em questão. Deve-se considerar o fato de utilização dessas técnicas para problemas maiores e mais complexos, onde essa diferença pode ser significativa.
Conclusão
O melhor modelo ajustado foi o modelo 3 (Spurr), que apresentou a melhor estatística na estimativa do volume para as 40 espécies testadas, já a melhor rede foi a 299 configurada com 15 neurônios na camada intermediária e função de ativação sigmoide.
Embora ambas as técnicas sejam consistentes, o desempenho das RNAs na predição volumétrica das espécies nativas apresentou critérios estatísticos superiores aos advindos do modelo 3 (Spurr) através da regressão tradicional, apresentando melhor adequação aos dados e melhor predição da variável desejada.
As redes neurais artificiais multicamada direta, podem ser uma excelente alternativa para a estimação do volume comercial de espécies florestais e, podem contribuir sobremaneira para a eficácia da solução desse importante problema.