Introduction
Solving mathematical problems requires several cognitive processes, including attention, memory, reasoning, and decision-making, among others because subjects must recall previously-learned mathematical rules, understand the problems presented, and perform the calculations required to solve them (Juidías & Rodríguez, 2007).
Several subcortical and cortical areas have been implicated in the cognitive processing of mathematical. Neuroimaging techniques have highlighted the brain areas associated with mathematical processing. One of these structures is the horizontal intraparietal sulcus associated with the semantic recognition of numbers and basic arithmetical problems (Ansari, 2016; Dehaene et al., 2004; Le Clec’H et al., 2000; Simon et al., 2004). Other cerebral areas have been associated with the modality in which problems are presented. For example, mathematical problems posed verbally (in sentence form) are associated with activation of the temporal lobe, while those displayed in a visual mode have been seen to generate higher activation in the occipital lobe (Eger et al., 2003; Prabhakaran et al., 2001). Activation of the temporal lobe has also been obtained during the recovery of automatized operations like simple multiplications compared to more complex ones (Zago et al., 2001). As a crucial area involved in the executive functions, the prefrontal cortex is associated with the quantities involved, the number of steps required to obtain the answer, and the style in which the problem is presented (Prabhakaran et al., 2001; Zago et al., 2001). Activation of the prefrontal cortex is observed when subjects are engaged in mental calculations as well as during manipulation of the information necessary to solve a problem.
Cognitive training entails the repetitive practice of certain tasks or regular activities. It may be oriented towards maintaining or improving an individual’s cognitive abilities, and generally consists of repetitive exercises designed to improve single (e.g., memory) or multiple (e.g., memory and reasoning) cognitive abilities. Some reports indicate that cognitive training enhances cognitive capacity (Sánchez-Pérez et al., 2018; Kueider et al., 2014) and the ability to improve performance in solving math problems. Published reports also suggest that the benefits of this particular type of training are more significant and long-lasting when the process includes working on multiple tasks rather than a single task (Anguera et al., 2013; Jaeggi et al., 2011). Also, benefits can be extended to other, untrained, cognitive abilities (e.g., enhancing sustained attention and working memory). Earlier research has shown that gradually increasing the complexity of the tasks used in training provides better results than training with tasks of similar complexity during all sessions, thus inducing better learning transfer (Van Merriënboer et al., 2006; Wickens et al., 2013). However, the benefits of cognitive training depend on several factors, including the number of sessions (Jaeggi et al., 2008), participants’ age (Dahlin et al., 2008), and individual differences in training performance (Jaeggi et al., 2011).
Significant differences in the effect of training have also been reported concerning task complexity and the form in which the complex tasks are presented. For example, partial versus whole-tasks (Roessingh et al., 2002; Van Merriënboer et al., 2006). Several studies have evaluated the benefits of cognitive training, but their analyses have focused primarily on the behavioral level (Jaeggi et al., 2011; Dahlin et al., 2008; Sánchez-Pérez et al., 2018), with only a few exploring the level of brain functionality using electroencephalographic (EEG) recording (Anguera et al., 2013).
EEG recording is one of several techniques that have been employed to determine cerebral functionality. This technique is defined as a mixture of rhythmic sinusoidal-like voltage fluctuations generated by the brain. The analysis of brain waves (John et al., 1977) and the degree of EEG synchronization between two structures over the time domain is called correlation (rEEG). This measure makes it possible to obtain information on brain functioning during different behavioral and cognitive states (see Guevara & Corsi-Cabrera, 1996 on correlation and coherence differences). In fact, neural oscillations at specific frequency bands are related to certain cognitive processes. For instance, the delta band (frequencies < 4 Hz with high amplitude) has been associated with internal processing during the performance of mental tasks (Fernández et al., 1995; Harmony et al., 1996; Vogel et al., 1968; Harmony, 2013), whereas theta (4-8 Hz) has been related to the coding phase of short-term memory tasks (Klimesch et al., 1996), maintenance (Sarnthein et al.,1998), information retrieval (Klimesch, et al., 2001), and differences in memory load (Sauseng et al., 2008). Changes in the alpha range (8-13 Hz with variable amplitude) and minor correlations between frontal regions in this band have been associated with attention processes and the inhibition of irrelevant information (Cooper et al., 2003; Foxe & Snyder 2011; Payne et al., 2013; Sauseng et al., 2008). In contrast, the fast bands with low amplitude such as beta (13-35 Hz) and gamma (31-60 Hz) have been related to inter-neuronal communication of inhibitory networks (Whittington et al., 2000) and high executive demands (Başar et al., 2001; Ramos et al., 1993). Ranges around 40 Hz have been associated with higher cognitive processes (Paul et al., 2005; Haig et al., 2000; Jefferys et al., 1996; Sauve, 1999), and gamma phase synchrony is considered an index of integrative network processing (Phillips & Singer, 1997), reflected mainly over frontal and prefrontal sites (Başar-Eroglu et al., 1996). During the solving of logical-mathematical problems, a coupling of the alpha2 band (10-13 Hz) in the parietal cortex with the theta band in dorsolateral prefrontal regions has been associated with arithmetic processes like substruction, number manipulations, and memory load (Dimitriadis et al., 2016; Rodríguez-Larios et al., 2020).
Regarding cognitive training (Anguera et al., 2013) showed an increase in the absolute power (AP) of the theta band in frontocentral regions after multi-task cognitive training compared to a group without training. These studies have reported the participation of the main regions linked to arithmetic process, such as the temporal, parietal, and frontal lobes, mainly over alpha and theta frequencies, which are shown to be involved in cognitive processes and training. However, these processes require the functional coupling of various brain regions (Pribram & Luria, 1973; Thatcher et al., 1986). Indeed, the complex processes of mathematical reasoning and training require functional synchronization among several cortical and subcortical cerebral areas defined not only by anatomical pathways but also by the synchrony of neural activity that occurs among distant areas during cognitive states.
The analysis of rEEG is one of the most common methods used to quantify EEG synchrony (Dauwels et al., 2010; Alba et al., 2007). This is a mathematical index that allows researchers to determine the degree of synchronization between the EEG signals emitted by two structures that may be associated through functional coupling (Shaw, 1981). In this regard, for example, an increased synchrony of EEG connectivity has been reported between left dorsolateral and parietal regions during the solving of complex word problems compared to simple ones (Molina et al., 2019).
An increased EEG correlation is considered an index of the use of greater neural resources (Volke et al., 2001), while a decreased correlation indicates that fewer resources are being utilized (Buschkuehl et al., 2012; Pinho et al., 2014; Tomasino et al., 2013). Studies of cognitive training have demonstrated that this approach does indeed enhance the abilities of trainees with increases in cognitive abilities that may be associated with the use of greater neural resources, possibly manifested as a higher degree of EEG correlation among several cortical areas (Jaušovec & Jaušovec, 2012).
Significant differences in the effects of cognitive training have been reported in relation to task complexity. Also, the prefrontal and parietal cortices play pivotal roles in reasoning and cognitive abilities. Based on this, this work aimed to determine the effect of cognitive training that included a gradual increase in the complexity of the math problems presented on the degree of EEG correlation between the prefrontal and parietal cortices while subjects solved complex math problems. The hypothesis points out that during the solving of such complex logical-mathematical word problems an increased EEG coupling (correlation) between prefrontal and parietal areas will be observed in young men after training with a paradigm based on a gradual increase in task complexity compared to a group trained with math problems of a uniform level of complexity. In addition, considering that the fast frequencies are associated with reasoning and high executive functions, this increased correlation between the prefrontal and parietal cortices was expected to occur mainly in the beta and gamma bands.
Method
Participants
Participants were 30 young men with a mean age of 20.27 (SD = 2.5), healthy, and right- handed with no prior history of neurological or psychiatric disorders, learning disabilities, drug abuse, or chronic illness. Gender selection was made considering the longitudinal design in order to reduce the variation over the different sessions that could occur due to women’s menstrual cycle (Kashuba & Nafziger, 1998; Bazanova et al., 2014). Subjects’ IQs were equal to or greater than 80, evaluated by the Shipley-2 intelligence scale (Shipley et al., 2009). They showed normal attention levels according to the parameters of the NEUROPSI memory and attention test (Ostrosky et al., 2012). Subjects were instructed to refrain from drinking caffeine or alcohol during the 12 hours before the EEG-recording session. All participants signed the informed consent according to the guidelines of the Ethics Committee at the Neuroscience Institute of the University of Guadalajara, Jalisco, Mexico. All procedures involved in the present experiment were approved by the institutional committee and performed in strict accordance with the Code of Ethics of the World Medical Association in the Helsinki Declaration (Rickham, 1964), and its later amendments, or comparable ethical standards, as well as APA ethical standards.
Procedure
Evaluation task. All participants solved an evaluation task to determine their performance during the solving of complex logical-mathematical word problems. This task was applied previously to assign the subjects to the training group, and again post-training. The evaluation consisted of solving 20 complex math problems in each session (held between 10:00 a.m. and 12:00 p.m.). The math problems were presented on a 32-inch computer screen placed at a distance of about 1.5 meters. The problems in sentence form, as well as proposed answers (in numeric values), were presented simultaneously on the screen. Participants had to verify whether those answers were correct or incorrect, and then press one of two keys on a computer keyboard: “B” if it is correct, “M” if it is not. Once a participant pressed a key to indicate his answer, the next problem appeared (see Figure 1A). The complex math problems included two-digit quantities. Arriving at the answer required performing three or more operations. The formula of the problems was x = a+(a-b)+[{a+(a-b)}+c]. For example, “John scored 45 points for his team, 10 more than Joseph. Marie scored 13 more points than John and Joseph together. How many points did they score in total?” The parameters analyzed for this evaluation task were the number of correct answers and total response times. The latter defined as the period between the moment when the problem appeared on the screen and when the participant touched the key to giving his answer. This same paradigm of the evaluation task was applied to the participants before (pre-training) and after (post-training) the cognitive training sessions.
Training sessions. Participants were randomly assigned to two types of training: a simple training group (ST, n = 15) with only math problems from the simplest level, and a complex training group (CT, n = 15) where the complexity of the math problems proposed increased gradually. Both types of training were performed during 18 sessions spread over nine weeks with two sessions per week. In each session, participants were seated in a comfortable room without noise or other distractors. They began by watching an instructional video on a laptop with a 13-inch screen that presented the steps required to solve the math problems. After that, they had to solve 25 words problems from the corresponding level, following those instructions (Figure 1B). The problems were presented under the same conditions as on the evaluation task. The only difference was that during the training sessions a feedback screen was presented after each answer with the appropriate “correct” or “incorrect” message.
For the CT group, the level of complexity of the math problems was increased gradually according to three factors: the number of digits (one or two), the number of operations required to solve the problems (one-five), and the morphosyntax with which the problems were written (i.e., x minus y or x less than y). These combinations gave a total of 18 complexity levels, one for each session. For the ST group, only simple-level problems were presented during all 18 sessions. Those problems consisted of one-digit quantities and required only one operation (i.e., x=a+b) to obtain the answer (Figure 2).
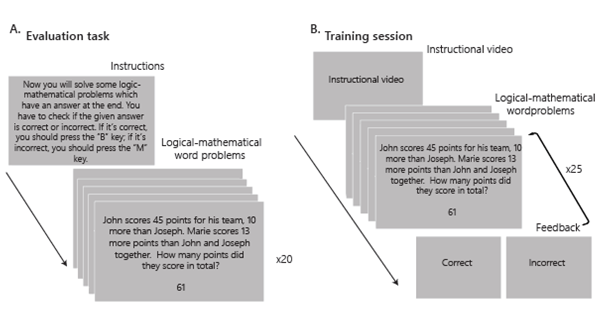
Note. A. Sequence of the evaluation task used in the pre- and post- training sessions (20 problems). B. Sequence used during each training session (25 problems each day)
Figure 1. Task and Training Design
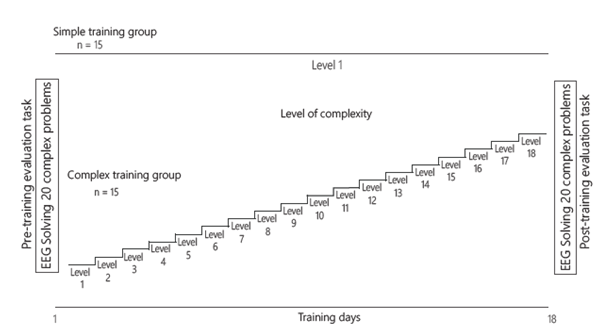
Note. Temporal representation of the training processes indicating the gradual increase of the complexity of the mathematical problems in the CT group and no increased complexity in the ST group
Figure 2. Training sessions.
EEG procedure. For EEG recording, electrode placement followed the international 10-20 system (Jasper, 1958). In accordance with the aims of the study, the recording sites were frontopolar (Fp1 and Fp2), prefrontal dorsolateral (F3 and F4), and parietal areas (P3, P4; Herwig et al., 2003; Homan, 1987; Okamoto et al., 2004). All derivations were referred ipsilaterally with the ground electrode placed on the forehead. EEGs were recorded using a NEXUS 32 device at 24 bits resolution with filters set at 1-50 Hz. Impedance for the EEG electrodes was maintained below 10 kohms. BioTrace+® software was used to sample (512 Hz) and store the EEG data for offline processing. In each recording session, participants were awake in a sitting position with their heads supported by the headrest of a comfortable chair. EEGs were recorded continuously while they solved 20 complex math problems from the evaluation task in both the pre- and post-training conditions.
The EEG recordings of each participant in each group were examined offline to identify saturated epochs or those that showed noise due to muscle activity, eye movement, or heartbeat. Those epochs were removed manually by visual inspection using a computer program (CHECASEN; Guevara et al., 2010). An offline digital filter was applied for the frequencies below 1 Hz and above 50 Hz using another computer program (FILDIG; Guevara et al., 2005). All artifact-free EEG segments were analyzed using the EEGmagic computer program (Guevara & Hernández-González, 2009), which applied fast Fourier transform to calculate the absolute power in each band. Next, the instant spectrum of each derivation in each band was obtained to calculate the electroencephalographic correlation between derivations for the intrahemispheric (Fp1-F3, Fp1-P3, F3-P3, Fp2-F4, Fp2-P4, F4-P4) and interhemispheric (Fp1-Fp2, F3-F4, P3-P4) correlations (r) for six frequency EEG bands: delta (δ, 1.5-3.5 Hz), theta (θ, 3.5-7.5 Hz), alpha1 (α1, 7.5-10.5 Hz), alpha2 (α2, 10.5-13.5 Hz), beta1 (β1, 13.5-19.5 Hz), beta2 (β2, 19.5-30 Hz), and gamma (γ, 31-50 Hz), using Pearson’s correlation coefficient.
Data analysis.For the behavioral data, the number of correct answers and response times were compared between groups by means of a t-test. The statistical analysis to compare the effects of each type of training was made only with the EEG data recorded during the solving of mathematical problems post-training. A mean of 255, 2-sec EEG segments from the post- training session were selected for analysis and aligned to the reading of the first problem. EEGs were then recorded continuously during all the math problems presented to both groups in the post-training sessions. This alignment was used with all 20 problems to ensure that the EEGs obtained were representative of subjects’ reading and comprehension, and of the solving of each problem. During the posterior analysis of the signals, EEG segments were selected manually and randomly from the entire duration of the post-training session, taking care to include segments representative of the reading, and solving both types of problems.
Before conducting the statistical analyses, and in order to approximate a normal distribution, the correlation values were transformed into Fisher’s Z values. A means comparison between two groups (ST versus CT) was used employing a t-test and considering a significance level equal or below to p value of .05 for all comparisons. Bonferroni correction for multiple comparisons suggested a p value of < .00833 as significant. The effect sizes (d) of the statistical tests were calculated following Cohen (1988). To confirm that there were no between-group differences at the beginning of the experiment, an a posteriori analysis for independent groups was performed.
Results
Behavioral data
The number of correct answers and response times recorded in the post-training condition were compared between the two study groups. A significant difference was observed since the ST participants had fewer correct answers (t = 3.58086, p = .00138, Cohen´s d = 1.353437) after the training sessions than those in CT (Figure 3). However, no differences were obtained for response
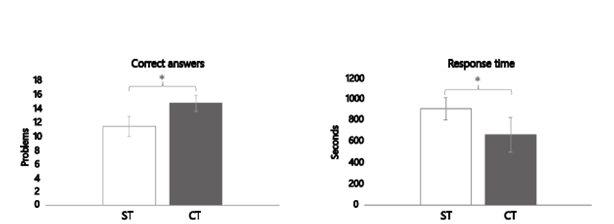
Note. Correct answers = ST (M = 11.53), CT(M = 13.84) and response time (in seconds)= ST (M = 939.60), CT (M = 770.59) obtained during performance of the post-training evaluation task for both groups.
ST = Simple Training, CT = Complex Training
* p < .05
Figure 3. Behavioral Results
Electroencephalographic results
While solving the mathematical word problems post-training, the CT group presented a higher intrahemispheric correlation between left frontopolar and parietal derivations (Fp1-P3) in almost all EEG bands: [delta (t = -2.595, p = .014, Cohen´s d = .947), alpha1 (t = -2.640, p = .013, d = .965), alpha2 (t = -2.255, p = .032, d = .823), beta1 (t = -2.242, p = .033, d = .818), beta2 (t = -2.490, p = .018, d = .912), and gamma (t = -2.673, p = .012, d = .980)], compared to the ST group. A similar increase in the intrahemispheric correlation was observed during the post-training assessment in the CT group between the left prefrontal and parietal cortices (F3-P3), though only in the alpha1 band (t = -2.677, p = .012, d = .972), also compared to ST (Figure 4).
No significant differences were obtained for the interhemispheric correlation between groups post-training at any derivation.
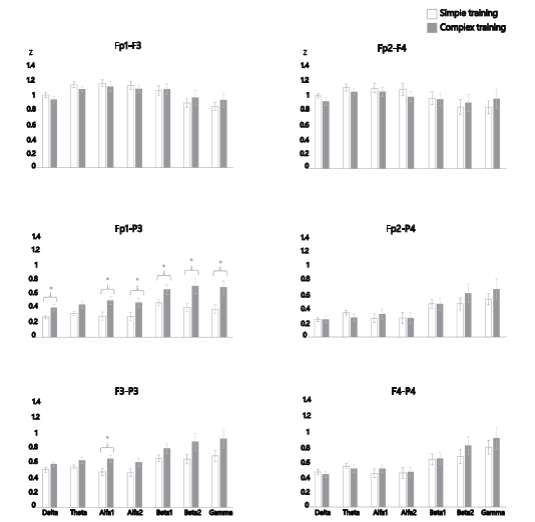
Note. Mean ± 1 SE of the intrahemispheric correlation (in z values) between the left (Fp1-F3, Fp1-P3, F3-P3) and right (Fp2-F4, Fp2-P4, F4-P4) derivations for the different frequency bands recorded in young men while solving complex logical-mathematical word problems on the post-training evaluation task
* p < .05 as compared to ST group. SE = Standard Error
Figure 4. Intrahemispheric Correlation
Discussion
This study showed that after cognitive training with a gradual increase in the complexity of the logical-mathematical problems presented, participants had better behavioral performance while solving complex math problems. These results were associated with a higher degree of EEG correlation between the prefrontal and parietal cortices of the left hemisphere.
After the 18 training sessions, participants in the CT group (gradual increase of complexity) showed benefits in their performance in solving math problems, as indicated by a higher number of correct answers than the subjects who were trained without increased complexity. These behavioral differences in the number of correct answers between ST and CT could, therefore, be linked to the kind of training provided. Previous reports have stated that training with a gradual increase of difficulty has greater benefits than working with more difficult exercises, but of a uniform level (Roessingh et al., 2002; Wulf & Shea, 2002). Accordingly, the benefits obtained from training with gradually increased difficulty (CT group) improved the transfer of skills from session to session and from one level of difficulty to the next, until they were finally applied to the most difficult problems. Thus, it is probable that the better performance by CT resulted from the enhanced strategies that those young men developed as a result of the group’s familiarity with such problems.
Although the ST subjects were allowed to practice in each session, the kinds of problems they were given to work on did not match the complexity of those presented on the evaluation task. In other words, they confronted a condition that demanded a distinct kind of processing to solve the complex problems posed. In the ST group, the level of skill obtained from simple, repetitive training with no increase in difficulty was shown to have no effect when those subjects were faced with solving more complex problems, likely as a consequence of deficient problem-solving skills or lower motivation after working on trivial word problems during the 18 training sessions.
Regarding differences in the EEG recordings, a higher correlation was observed in the CT group while solving complex math problems on the post-training evaluation task. This increased intrahemispheric correlation appeared only between the left prefrontal and parietal regions. Solving the complex problems presented in the study required active manipulation of the information that included syntactic interpretation of the word problem, numerical processing of the quantities involved, and mental manipulations according to the number and type of operations required, all of which meant that subjects had to read the problem more than once. Hence, it is probable that the sequence of events required to solve those complex problems is related to a predominant synchronization of the left hemisphere, which has been implicated previously in the processing of the verbal features of problems (Graves et al., 2014; Molina et al., 2019).
The activation and synchronization observed in the left hemisphere were present over both slow and fast EEG bands. Descriptions of those bands have been linked to various processes. Increased alpha band activity over frontal regions has been observed posterior to cognitive training with working memory tasks, especially dual n-back tasks (Blacker et al., 2017), and in parietal regions of participants working with spatial n-back tasks (Gevins et al., 1997). Neurofeedback training employed to maintain and enhance 14-18 Hz frequency activity, meanwhile, has shown changes in frontal beta band activity with coherence among prefrontal dorsolateral derivations (Cannon & Lubar, 2007). Similarly, the fast bands have been associated with higher cognitive processes (Paul et al., 2005; Haig et al., 2000; Jefferys et al., 1996; Sauve, 1999; Phillips & Singer, 1997).
The functional collaboration between prefrontal and parietal regions has been associated with processes that involve attention, memory recovery, working memory, information manipulation (Naghavi & Nyberg, 2005; Campo et al., 2005; Babiloni et al., 2004; Sauseng et al., 2008), and with the process of solving math problems (Zago et al., 2001; Prabhakaran et al., 2001; Dimitriadis et al., 2016). The increased use of these skills in each succeeding training session and their repeated application in each one could be manifested in an enhanced synchronization of the brain areas, given that this is the representation of plastic changes in functional connectivity linked to the recruitment of greater cognitive resources (Volke et al., 2001) that is reflected in improved performance.
The functional coupling between fronto-polar and parietal regions observed in our data could be linked to the characteristics of the logical-mathematical problems presented, which involved increasing levels of abstraction and complexity to achieve sub-goals that led to solving them (Christoff et al., 2009). Changes in the functional coupling of these regions have been linked to the effect of multi-task training, mainly as an increased coherence between frontal and parietal regions in the theta (Anguera et al., 2013; Klingberg, 2010; Langer et al., 2013) and alpha bands (Dimitriadis et al., 2016).
There are also reports that cognitive training with greater cognitive load leads to enhanced behavioral performance compared to tasks with lower cognitive demand (Anguera et al., 2013; von Bastian & Oberauer, 2013). In line with this, the better behavioral performance observed in CT in our study could be related to changes in the degree of coupling that occurred between cortical regions after complex training. In other words, the effects of cognitive training seemed to improve the solving of logical-mathematical problems and increase synchronization among areas of the left hemisphere, especially between prefrontal and parietal regions.
The higher correlation between left prefrontal and parietal regions observed in the slow and fast bands during the solving of the logical-mathematical problems post-training may also be associated with several cognitive processes. For example, an increased capacity to keep and handle multiple items of information and to recall the mathematical rules necessary to solve the problems, as well as with complex cognitive processes like arithmetical operations and active work with verbal and numerical elements. However, this is a proposal to investigate in future experiments.
According to the results, better performance in solving logical-mathematical word problems manifested in both behavioral and electrophysiological parameters was observed after increased complexity training. The increased degree of EEG correlation between the prefrontal and parietal cortices could reflect the use of greater neural resources associated with the cognitive abilities acquired after cognitive training. Taken together, these data suggest that the functional synchronization between the left prefrontal and parietal cortices plays an important role in enhancing subjects’ ability to solve math problems after receiving cognitive training.
Finally, it is important to recognize the limitations of the study regarding future research. First, these results must be interpreted with caution because several of the p-values were not submitted to the multiple comparisons correction method. According to de Peralta-Menendez et al. (2004) method of corrections for multiple comparisons, the six electrodes used only allowed us to consider as significant p < .05/6 (p < .00833). However, it preferred to indicate all differences without this correction, though this might increase the level of speculation in some cases. The procedure applied in this study did not allow us to associate EEG patterns with specific cognitive processes during the solving of the mathematical word problems, thus in future work, it would be pertinent to evaluate EEG changes in relation to the specific steps involved in solving each type of problem. This approach could facilitate obtaining a more precise relation between correlation values and the possible cognitive processes involved.
Another limitation is the number of subjects in each group, as this was a longitudinal study and several of the initial, participants did not complete the entire training program. Unfortunately, desertion was substantial. Another important characteristic to consider when attempting to extrapolate our results to other populations is that participants were undergraduate students with low mathematical load in their formation. Future research should strive to include a second evaluation with a latency period after the initial one in order to ascertain the long-term effects of training. A population with greater math skills, and other educational levels, ages, and gender that considers variables such as motivation should also be considered.