Introducción
Desde finales del siglo XX, con la aparición de avances científicos y tecnológicos, se han producido cambios en una gran variedad de contextos, y han adquirido una gran importancia la estadística y la probabilidad (Batanero et al., 2011). Desde esta perspectiva, existe una brecha de conocimiento en cuanto a la estadística y a la probabilidad se refiere, debido a que, durante años, no se consideró una necesidad. Desde este prisma, la ausencia de formación por parte del profesorado y futuro personal docente ha provocado un escaso conocimiento de los conceptos y procedimientos de la estadística y la probabilidad (Batanero, 2009). Ante esta situación, el dominio del profesorado en relación con los conocimientos que debe tener para enseñar estadística y probabilidad son claves para realizar un proceso de enseñanza-aprendizaje eficaz. En este sentido, el profesorado requiere de conocimientos técnicos y estratégicos para dar respuesta a las necesidades formativas del alumnado (Anasagasti y Berciano, 2016). En otras palabras, la escuela juntamente con el profesorado debe adaptar y reestructurar su sistema educativo para ofrecer una enseñanza de calidad desde distintos contextos de aprendizaje (Alsina, 2019; Jiménez y Jiménez, 2005). En otras palabras, el profesorado no debe basar toda la práctica de enseñanza mayoritariamente en el libro de texto (Cabero et al., 1989; García Mateos y Caballero García, 2005).
Desde esta perspectiva, en esta investigación se asumen los planteamientos del enfoque de los itinerarios de enseñanza de las matemáticas (Alsina, 2019, 2020a, 2020b) como estrategia didáctica para ofrecer una enseñanza-aprendizaje de la estadística y la probabilidad desde distintos contextos de aprendizaje: 1) contextos informales (situaciones de la vida cotidiana, materiales manipulativos y juegos); 2) contextos intermedios (recursos tecnológicos); 3) contextos formales (recursos gráficos). La finalidad de este estudio es pre-
sentar el proceso de diseño, construcción y validación de un cuestionario para evaluar aspectos relevantes del conocimiento del profesorado de educación primaria en su enseñanza de estadística y probabilidad. Para ello, se consideró el modelo del conocimiento especializado del profesorado de matemáticas (MTSK, por sus siglas en inglés) (Carrillo et al., 2018), en el marco de los planteamientos del enfoque de los itinerarios de enseñanza de las matemáticas (Alsina, 2018, 2019, 2020a).
Marco teórico
De acuerdo con la finalidad del estudio, se hace una revisión de la bibliografía en tres ámbitos interrelacionados. En concreto, se vincula el conocimiento del profesorado, en activo, en estadística y probabilidad con el enfoque de los itinerarios de enseñanza de las matemáticas, haciendo especial hincapié en los dominios y subdominios del modelo MTSK.
Conocimiento especializado del profesorado de matemáticas MTSK
Desde la propuesta de Shulman (1987), acerca de los conocimientos del profesorado para enseñar, se han realizado numerosos estudios, y con estos, han ido evolucionando diferentes modelos de conocimiento, hasta convertirse en un tema fundamental a investigar por parte de la comunidad investigadora en educación matemática (Aguilar-González, et al., 2018).
El modelo Mathematics Teacher's Specialised Knowledge (MTSK) de Carrillo et al. (2018) focaliza su estudio en la enseñanza de las matemáticas para comprender el conocimiento del profesorado y, a su vez, sirve de herramienta metodológica para analizar diferentes prácticas a través de los distintos dominios del conocimiento (Carrillo et al., 2017).
En el modelo MTSK, a diferencia del MKT, se entiende que la especialización del conocimiento del profesorado procede de su profesión, en este caso, la enseñanza de las matemáticas. Además, el modelo está conceptualizado con base en el hecho de que se usará este modelo para la comprensión del conocimiento que el profesorado de matemáticas usa para enseñar los contenidos de esta materia (Carrillo, et al., 2018; Catalán, et al., 2015; Climent y Martín-Díaz, 2022). Desde esta perspectiva, Carrillo y su equipo manifiestan que, en el modelo MKT, es difusa la comprensión del conocimiento que se utiliza para enseñar los distintos contenidos.
El modelo MTSK (Figura 1), siguiendo la línea de Shulman (1986) y sus predecesores, propone dos dominios de conocimiento para su análisis: conocimiento matemático (MK) y conocimiento didáctico del contenido (PCK) que, a su vez, se dividen en tres subdominios.

Figura 1 Modelo teórico del conocimiento especializado del profesorado de matemáticas, MTSK (Carrillo et al., 2018).
El MK comprende el contenido matemático en el subdominio conocimiento de los temas (KoT), las conexiones entre contenidos en el conocimiento de la estructura de las matemáticas (KSM) y las formas de hacer o crear matemáticas en el conocimiento de la práctica matemática (KPM). Por su parte, el PCK comprende el conocimiento del profesorado del contenido matemático como objeto de enseñanza en el conocimiento de la enseñanza de las matemáticas (KMT), como objeto de aprendizaje en el conocimiento de las características del aprendizaje de las matemáticas, (KFLM) y desde los estándares de aprendizaje que se esperan alcanzar en un curso o nivel educativo determinado en el conocimiento de los estándares de aprendizaje de las matemáticas (KMLS).
En este estudio se vincula el modelo MTSK con el enfoque de los itinerarios de enseñanza de las matemáticas (Alsina, 2018, 2019, 2020a), que se describe en el próximo apartado. En este sentido, se conectan los subdominios del MTSK (KoT, KSM, KTM, KMLS, KFLM) con los distintos contextos y recursos del EIEM (reales, recursos manipulables, juegos, recursos tecnológicos, recursos gráficos).
El enfoque de los itinerarios de enseñanza de las matemáticas
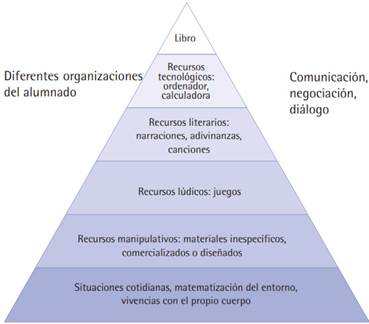
Este enfoque pretende ser una herramienta para ayudar al profesorado a desarrollar la competencia matemática de sus estudiantes, partiendo de la base que para empoderar esta competencia se requiere diversificar los contextos de enseñanza-aprendizaje. El EIEM tiene su origen en el diagrama piramidal (Figura 2), en el que se especifican los distintos contextos de enseñanza, organizados según su frecuencia de uso: los niveles 1, 2 y 3 deberían ser utilizados con mayor periodicidad que los niveles 4, 5 y 6 (Alsina, 2010).
En este sentido, este enfoque parte de la necesidad de fomentar la comprensión más que la mera memorización, la actividad heurística más que la pura ejercitación, o el pensamiento matemático crítico más que la simple repetición (Alsina, 2019).
El enfoque de los itinerarios de enseñanza se fundamenta en tres pilares relacionados: la perspectiva sociocultural del aprendizaje humano (Vygotsky, 1978); el modelo de formación realista-reflexivo (Melief et al., 2010; Tigchelaar et al., 2010), adaptado a la formación del profesorado de matemáticas (Alsina, 2019); y la educación matemática realista (EMR) de Freudenthal (1991). Tomando en consideración los subdominios del modelo MTSK, esta fundamentación se vincula al conocimiento de las características del aprendizaje de las matemáticas (KFLM), al considerar cómo se aprenden y piensan los contenidos matemáticos, así como las distintas formas que tiene el alumnado de interactuar con cada contenido (Flores-Medrano et al., 2016).
Desde esta perspectiva, según afirma Alsina (2020b), el EIEM plantea que el desarrollo del pensamiento matemático se debería llevar a cabo a través de itinerarios de enseñanza, entendiendo por itinerario una secuencia de enseñanza intencionada que contempla tres niveles: 1) contextos informales, que permiten visualizar las ideas matemáticas de manera concreta (situaciones manipulativos y juegos); 2) contextos intermedios, que a través de la exploración y la reflexión conducen a la esquematización y generalización progresiva del conocimiento matemático (recursos literarios y tecnológicos); y 3) contextos formales, en los que se trabaja la representación y formalización del conocimiento matemático con procedimientos y notaciones convencionales para completar de esta forma el aprendizaje desde lo concreto hasta lo simbólico (recursos gráficos). En este sentido, la enseñanza contemplada en tres niveles se vincula con el subdominio, conocimiento de los temas (KoT) donde se incluyen aspectos que permiten relacionarlos con contextos reales o con el propio contenido matemático en forma de ejemplos (Muñoz-Catalán, et al., 2015). Asimismo, el conocimiento de la enseñanza de las matemáticas (KMT) se relaciona con los distintos recursos utilizados para enseñar en los distintos niveles (situaciones de vida cotidiana, materiales manipulativos, juegos, recursos literarios, tecnológicos y recursos de vida cotidiana, materiales manipulativos, juegos, recursos literarios, tecnológicos y recursos
gráficos). En este sentido, Muñoz-Catalán y sus colaboradores (2015) afirman que, en el KMT, adquiere mucha importancia el conocimiento de distintos recursos para la enseñanza de las matemáticas.
Antecedentes del conocimiento del profesorado para enseñar estadística y probabilidad
Los estudios sobre el conocimiento del profesorado y su enseñanza de la estadística y la probabilidad son escasos, y más los que consideran al profesorado en activo de Educación Primaria. Respecto a las investigaciones que abordan el análisis del conocimiento del profesorado para enseñar estadística y probabilidad desde el marco del MTSK, que es la línea en la que nos interesa profundizar en este trabajo, no se han encontrado investigaciones que analicen el conocimiento del profesorado en activo en la enseñanza de la estadística y la probabilidad. En este sentido, solo se encontró un estudio con futuro profesorado en el que se analizan los subdominios KoT, KFLM y KMLS del modelo MTSK.
En un estudio anterior, se han localizado, en total, 34 artículos durante el periodo de 1997-2021 que abordan el análisis de los conocimientos del profesorado para enseñar estadística y probabilidad (Franco y Alsina, 2022). De todos los artículos identificados, 22 se centran en futuro profesorado y 12 en profesorado en activo.
Respecto al segundo grupo de estudios, 4 de los estudios identificados han analizado el conocimiento de la estadística (2) y la probabilidad (2) desde el modelo MKT de Ball y sus colaboradores (2008); 4 de las investigaciones han utilizado el modelo CCDM de Godino y su equipo (2017) para analizar el conocimiento del profesorado en la enseñanza de la probabilidad; y, 4 artículos analizan el conocimiento sin un modelo específico, encontrando 2 artículos en la enseñanza de la estadística y 2 en la enseñanza de la probabilidad.
Por lo que se refiere a los resultados obtenidos, la mayoría de investigaciones muestran puntuaciones bajas en los subdominios y facetas de conocimiento analizadas, lo cual refleja un escaso conocimiento del profesorado de Educación Primaria para enseñar estadística y probabilidad (Franco y Alsina, 2022). Por ejemplo, en el caso de la estadística, Siswono et al. (2018) administran un cuestionario sobre el concepto de media para analizar el PCK, CCK y SMK de 40 maestros y maestras de primaria en activo. Encontraron que la mayoría no comprende el concepto de media desde la perspectiva de un total fijo, con una disparidad de respuestas sobre la adecuación de la enseñanza y aprendizaje del concepto de media, mediana y moda en el alumnado de primaria. En una línea similar, Koleza y Kontogianni (2012) analizaron el conocimiento estadístico de 10 docentes de primaria, y hallaron un conocimiento deficitario en nociones como la mediana, la moda, el rango, el diagrama de tallo y el diagrama de línea.
En el caso de la probabilidad, Vásquez y Alsina (2017), por ejemplo, aplican un cuestionario sobre el conocimiento común de la probabilidad a 93 docentes en activo, encontraron un bajo conocimiento de los conceptos básicos sobre la probabilidad. Por su parte, Cardeñoso y Azcárate (2004) analizan las nociones de aleatoriedad y probabilidad a 598 maestros y maestras en activo, evidenciaron conocimientos deficitarios para la enseñanza de estos contenidos.
Los resultados de las investigaciones demuestran que el contenido didáctico matemático para la enseñanza de la estadística y probabilidad es escaso; presentan, en algunos casos, inseguridad para tratar los contenidos en el proceso de enseñanza-aprendizaje (Batanero, 2009, 2019; Vásquez y Alsina, 2015).
En este sentido, diversos estudios sugieren potenciar la formación en la enseñanza de estadística y probabilidad incorporando estrategias y recursos que aglutinen distintos contextos de aprendizaje: los proyectos estadísticos, los materiales manipulativos, los recursos tecnológicos o, más en general, los itinerarios de enseñanza a partir de distintos contextos (Azcárate et al., 1998; Batanero et al., 1997; Cardeñoso y Azcárate, 2004; Gea y Fernandes, 2018; Ortiz et al., 2006; Pinheiro et al., 2019; Vásquez y Alsina, 2015; entre otros).
Proceso de elaboración y validación de un cuestionario sobre el conocimiento especializado matemático del profesorado de Educación Primaria para enseñar estadística y probabilidad
Para analizar el conocimiento del profesorado en la enseñanza de estadística y probabilidad, se opta por un cuestionario de respuesta abierta, porque permite obtener respuestas con mayor riqueza y profundidad de quienes responden. El cuestionario se ha implementado a profesorado de educación primaria de las comunidades autónomas de Cataluña y Baleares, sea cual sea su conocimiento de estadística y probabilidad. Sin embargo, puede usarse en su formato actual con profesorado de cualquier país de habla hispana.
Para poder efectuar la elaboración y validación del cuestionario se han llevado a cabo diversas fases: 1) análisis del modelo de conocimiento MTSK; 2) Estudio de investigaciones sobre el enfoque de los itinerarios de enseñanza de las matemáticas; 3) revisión exhaustiva de la bibliografía existente sobre diferentes estudios destinados al conocimiento del profesorado en la enseñanza de estadística y probabilidad para profesorado en activo de educación primaria; 4) vinculación del modelo MTSK con el enfoque de los itinerarios de enseñanza de las matemáticas; 5) vinculación de los dominios, subdominios o facetas de conocimiento de los modelos Mathematical knowledge for Teaching (MKT) y el modelo de conocimientos y competencias didáctico-matemáticas (CCDM) con el MTSK; 6) análisis de los principales conocimientos que debería tener el profesorado para enseñar estadística y probabilidad; 7) la elaboración de la versión piloto del cuestionario; 8) la validación mediante el juicio experto y aplicación piloto; y 9) construcción de la versión final del instrumento, que se ha denominado ''Cuestionario MTSK-estocástico”. Las fases 1, 2, 3, 4, 5 contemplan la revisión de bibliografía e investigaciones que permiten diseñar el instrumento, mientras que las fases 6, 7 y 8 contemplan la construcción y validación del cuestionario.
Construcción de la versión piloto del Cuestionario MTSK-estocástico
Para la construcción de la versión piloto del instrumento, se revisó la bibliografía existente sobre el modelo MTSK y el enfoque de los itinerarios de enseñanza de las matemáticas y, posteriormente, sobre el conocimiento del profesorado para la enseñanza de la estadística y la probabilidad. Seguidamente, se examinaron los distintos instrumentos utilizados para evaluar el conocimiento del profesorado. Una vez finalizado el proceso de análisis, se seleccionaron distintos ítems siguiendo los siguientes criterios de inclusión:
Criterio de inclusión 1: Ítems con un contexto de enseñanza del EIEM
Criterio de inclusión 2: Ítems que se analicen los subdominios del MTSK
Criterio de inclusión 3: Ítems relacionados con contenido de la etapa de Educación Primaria
En total, se recopilaron 85 ítems, concretamente, 38 relacionados con el subdominio conocimiento de los temas (KoT), 10 ítems con el conocimiento de la estructura de las matemáticas (KSM), 4 con el conocimiento de la práctica matemática (KPM), 7 del conocimiento de la enseñanza de las matemáticas (KSM), 18 del conocimiento de las características del aprendizaje de las matemáticas (KFLM) y, 8 del conocimiento de los estándares de aprendizaje de las matemáticas (KMLS).
A partir de esta revisión bibliográfica, se analizaron y seleccionaron los ítems más adecuados para evaluar los dominios y subdominios del MTSK desde el planteamiento del EIEM. En concreto, se adaptaron tres ítems sobre el conocimiento de estadística y obtenidos de Estrella (2010), Siswono et al. (2018) y Estrella et al. (2015) y cuatro sobre el conocimiento de la probabilidad, procedentes de Estrella (2010), Vásquez y Alsina (2015), Begg y Edwards (1999) y Estrella, et al. (2015). El resto de ítems de la primera versión del cuestionario, dos de estadística y uno de probabilidad, fueron de creación propia.
Una vez elaborada esta primera versión, se solicitó la colaboración de ocho personas expertas procedentes de diferentes territorios del Estado español, para que llevaran a cabo una validación externa, teniendo en cuenta su experiencia profesional y su trayectoria laboral hasta la actualidad.
Revisión del Cuestionario MTSK-estocástico (mediante juicio experto y aplicación piloto
El instrumento se somete a un proceso de validación (Fase 4) mediante el juicio experto, lo cual permite comprobar si el instrumento cumple con los criterios de validez y fiabilidad requeridos para su correcta utilización.
Juicio experto
El juicio experto permitió realizar una evaluación cualitativa de los ítems, contrastando su validez en relación con el grado de correspondencia de cada uno con las dimensiones del conocimiento propuestas por el modelo MTSK. El juicio lo realizaron ocho personas expertas en didáctica de la matemática. Para ello, se ha entregado a cada una, por correo electrónico, un documento que incluye, la versión inicial del instrumento y una pauta para evaluar el grado de adecuación de acuerdo con el modelo MTSK.
El equipo experto analizó tres aspectos en relación con cada ítem: 1) grado de correspondencia, indicando si cada ítem pertenece, tienen dudas, o no pertenece a la categoría; 2) formulación, respecto a la claridad y al lenguaje utilizado en cada ítem, definiendo como adecuada, a mejorar, no adecuada, y 3) pertinencia, referida a la categoría del conocimiento evaluada, definiendo como pertinente, con dudas, no pertinente. Finalmente, disponían de una sección de comentarios o correcciones para indicar los motivos o propuestas de mejora de cada ítem.
Una vez recibido el juicio experto, se realizó un análisis descriptivo de la validez del contenido, a partir de los valores asignados a cada indicador para cada subdominio del MTSK, en función del grado de correspondencia, formulación y pertinencia. En la Tabla 1, se muestran las medias de las puntuaciones asignadas a cada indicador que constituye el instrumento de estadística.
Como se aprecia en la Tabla 1, las puntuaciones y opiniones de las personas expertas proporcionaron, en general, una valoración positiva en relación con los indicadores. No obstante, se han modificado o eliminado los ítems que obtuvieron una puntuación promedio inferior a 2,5 puntos. A partir de los datos obtenidos se modificó la redacción de los ítems 1b), 2a), 2b), 2c), 3b), 3c), 4b), 4d), 5a), 5c), 5d).
Ítem 1: se modificó el enunciado de la contextualización, se eliminó el enunciado 1e) y se mejoró la redacción del 1b) y 1d). Finalmente, se incluyó el subdominio KSM y KMLS en 1a), KMLS en 1c) y 1d).
Ítem 2: A petición de algunas personas expertas, se agregó información a la pregunta ¿Qué estrategias utilizaría para ayudar a estudiantes que no han sabido resolver el problema?, pues carecía de contexto la pregunta, por lo que se añadió: Si un alumno o alumna no entiende de dónde sale la frecuencia relativa de caramelos de un determinado color, ¿cuál sería su intervención? Además, se mejoró la formulación de la pregunta 2c.
Ítem 3: Se amplió la redacción del ítem 3, a petición de algunas personas expertas, pues manifiestan la importancia de explicar detalladamente el juego, para poder contestar el ítem con más facilidad. Seguidamente, se mejoró la redacción de 3b), 3e) y se reformuló 3c), ya que varias evaluaciones sugirieron añadir un ejemplo
Tabla 1 Puntuaciones asignadas por el grupo experto al Cuestionario MTSK-estocástico de estadística (n=9)
| Frecuencia de la puntuación cuestionario MTSK-estocástico estadística | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Correspondencia | Formulación | Pertinencia | ||||||||||
| ítem | Dimensión | Pertenece (3) | Con dudas (2) | No pertenece (1) | Adecuada (3) | Formulación A mejorar (2) | No adecuada (1) | Pertinente (3) | Pertinencia Con dudas (2) | No pertinente (1) | Media | |
| a) | KoT | 8 | 0 | 1 | 9 | 0 | 0 | 8 | 1 | 0 | 2,89 | |
| b) | KFLM | 9 | 0 | 0 | 6 | 3 | 0 | 9 | 0 | 0 | 2,89 | |
| 1 | c) | KMT | 8 | 1 | 0 | 8 | 1 | 0 | 9 | 0 | 0 | 2,93 |
| d) | KSM | 7 | 2 | 0 | 8 | 1 | 0 | 7 | 2 | 0 | 2,81 | |
| e) | KMLS | 6 | 1 | 2 | 8 | 1 | 0 | 8 | 1 | 0 | 2,74 | |
| a) | KLFM | 9 | 0 | 0 | 4 | 5 | 0 | 8 | 1 | 0 | 2,78 | |
| 2 | b) | KMT | 9 | 0 | 0 | 6 | 3 | 0 | 9 | 0 | 0 | 2,89 |
| c) | KMLS | 9 | 0 | 0 | 8 | 1 | 0 | 9 | 0 | 0 | 2,96 | |
| a) | KoT | 8 | 0 | 1 | 8 | 1 | 0 | 8 | 1 | 0 | 2,85 | |
| b) | KFLM | 9 | 0 | 0 | 6 | 3 | 0 | 9 | 0 | 0 | 2,89 | |
| 3 | c) | KMT | 8 | 1 | 0 | 8 | 1 | 0 | 9 | 0 | 0 | 2,92 |
| d) | KPM | 4 | 0 | 5 | 9 | 0 | 0 | 7 | 0 | 2 | 2,48 | |
| e) | KSM | 7 | 1 | 1 | 8 | 1 | 0 | 8 | 1 | 0 | 2,81 | |
| a) | KoT | 8 | 0 | 1 | 9 | 0 | 0 | 8 | 1 | 0 | 2,89 | |
| b) | KFLM | 9 | 0 | 0 | 6 | 3 | 0 | 9 | 0 | 0 | 2,89 | |
| 4 | c) | KPM | 4 | 0 | 5 | 9 | 0 | 0 | 7 | 0 | 2 | 2,48 |
| d) | KMT | 8 | 1 | 0 | 8 | 1 | 0 | 9 | 0 | 0 | 2,93 | |
| a) | KoT | 8 | 0 | 1 | 6 | 3 | 0 | 8 | 1 | 0 | 2,78 | |
| b) | KoT | 8 | 0 | 1 | 7 | 2 | 0 | 7 | 2 | 0 | 2,78 | |
| 5 | c) | KFLM | 9 | 0 | 0 | 6 | 3 | 0 | 9 | 0 | 0 | 2,89 |
| d) | KMT | 8 | 1 | 0 | 8 | 1 | 0 | 9 | 0 | 0 | 2,93 | |
| e) | KSM | 7 | 1 | 1 | 8 | 1 | 0 | 8 | 1 | 0 | 2,81 | |
Nota: Fuente propia de la investigación.
concreto para poder dar una intervención específica a dichas dificultades. Finalmente, se incluyó el subdominio KSM y KFLM en la pregunta 3a), se eliminó el subdominio KPM en la pregunta 3d) y se sustituyó por KMLS y KSM y, se eliminó la categoría KSM y se sustituyó por KMLS
Ítem 4: A petición de algunas personas expertas, se mejoró la redacción a la pregunta 4d) y 4b) al añadir ''comentadas en la pregunta 4b''y ''errores” respectivamente. Además, se añadió la categoría KFLM y KSM en 5a) y se sustituyó el subdominio KPM por KMLS en 5c)
Ítem 5: A petición de una persona experta, se añadió al enunciado del ítem la siguiente afirmación: Estos gráficos presentan una comparativa entre los datos anteriores al 10 de mayo y los posteriores al 11 de mayo, pues es un detalle importante que remarcar en el enunciado. Posteriormente, se mejoró la redacción de 5a), 5c) y 5d). Además, se sustituyó la categoría KoT por KFLM en la pregunta 5a) y el subdominio KSM por KMLS en la pregunta 5e). Además, se incluyó el subdominio KSM en la pregunta 5b).
En la Tabla 2 se muestran las medias de las puntuaciones asignadas por las personas expertas a cada indicador que constituye el instrumento de probabilidad.
Como se aprecia en la Tabla 2, las puntuaciones y opiniones expertas proporcionaron, en general, una valoración positiva en relación con los indicadores. No obstante, se han modificado o eliminado los ítems que obtuvieron una puntuación promedio inferior a 2,5 puntos. A partir de los datos obtenidos
Tabla 2 Puntuaciones asignadas por las personas expertas al cuestionario MTSK estocástico de probabilidad (n=9)
| Frecuencia de la puntuación cuestionario MTSK-estocástico probabilidad | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Correspondencia | Formulación | Pertinencia | ||||||||||
| ítem | Dimensión | Pertenece (3) | Con dudas (2) | No pertenece (1) | Adecuada (3) | A mejorar (2) | No adecuada (1) | Pertinente (3) | Con dudas (2) | No pertinente (1) | Media | |
| a) | KoT | 7 | 1 | 1 | 5 | 4 | 0 | 7 | 2 | 0 | 2,67 | |
| b) | KFLM | 9 | 0 | 0 | 7 | 2 | 0 | 9 | 0 | 0 | 2,93 | |
| 1 | c) | KMT | 9 | 0 | 0 | 6 | 3 | 0 | 9 | 0 | 0 | 2,89 |
| d) | KMLS | 9 | 0 | 0 | 7 | 2 | 0 | 6 | 3 | 0 | 2,81 | |
| e) | KSM | 6 | 2 | 1 | 8 | 0 | 0 | 6 | 2 | 0 | 2,56 | |
| a) | KoT | 9 | 0 | 0 | 7 | 2 | 0 | 7 | 2 | 0 | 2,85 | |
| b) | KoT | 8 | 0 | 1 | 9 | 0 | 0 | 8 | 1 | 0 | 2,89 | |
| 2 | c) | KFLM | 8 | 0 | 0 | 7 | 1 | 0 | 8 | 0 | 0 | 2,63 |
| d) | KMT | 8 | 1 | 0 | 5 | 4 | 0 | 9 | 0 | 0 | 2,81 | |
| e) | KSM | 6 | 2 | 1 | 8 | 1 | 0 | 7 | 2 | 0 | 2,74 | |
| a) | KoT | 9 | 0 | 0 | 7 | 2 | 0 | 8 | 1 | 0 | 2,89 | |
| 3 | b) | KFLM | 9 | 0 | 0 | 8 | 1 | 0 | 9 | 0 | 0 | 2,96 |
| c) | KMT | 7 | 2 | 0 | 6 | 3 | 0 | 8 | 1 | 0 | 2,78 | |
| a) | KoT | 9 | 0 | 0 | 5 | 4 | 0 | 8 | 1 | 0 | 2,81 | |
| b) | KFLM | 9 | 0 | 0 | 6 | 3 | 0 | 9 | 0 | 0 | 2,89 | |
| 4 | c) | KMT | 7 | 2 | 0 | 7 | 2 | 0 | 8 | 1 | 0 | 2,81 |
| d) | KPM | 4 | 0 | 5 | 5 | 0 | 4 | 7 | 0 | 2 | 2,19 | |
| e) | KLMS | 9 | 0 | 0 | 8 | 1 | 0 | 8 | 1 | 0 | 2,93 | |
| a) | KFLM | 9 | 0 | 0 | 6 | 3 | 0 | 9 | 0 | 0 | 2,89 | |
| b) | KPM | 4 | 0 | 5 | 8 | 1 | 0 | 7 | 0 | 2 | 2,44 | |
| 5 | c) | KMT | 8 | 1 | 0 | 5 | 4 | 0 | 9 | 0 | 0 | 2,81 |
| a) | KoT | 7 | 1 | 1 | 5 | 4 | 0 | 7 | 2 | 0 | 2,67 | |
Nota: Fuente propia de la investigación.
se descartaron los ítems 4d) u 5b) y se modificó la redacción de los ítems 1a), 1b), 1c), 1d), 2c), 2d), 2e), 3a), 3c), 4a), 4b), 5a) y 5c).
Ítem 1: Se eliminó el enunciado de 1a) y se mejoró la redacción de 1b), 1c), 1d). Finalmente, se incluyó el subdominio KMP y KMT a la pregunta 1a).
Ítem 2: Se modificó el enunciado 2a) y se agregó el subdominio KPM, se incorporó el KSM en el ítem 2b) y se mejoró la redacción de 2c), 2d) y 2e). Por último, se incluyó 2a) en la categoría del KPM, 2b) en la categoría KSM, 2d) en el KFLM y 2e) en el KMLS.
Ítem 3: Se modificó el enunciado y se mejoró la redacción del ítem 3, pues varias personas expertas comentaron que no se entendía el enunciado del ítem. En cuanto a las preguntas, se mejoró la redacción de 3a) y se reformuló 3c), ya que varias evaluaciones sugirieron añadir un ejemplo concreto para poder dar una retroalimentación adecuada. Además, se añadió 3ª) y 3c) a la categoría KPM.
Ítem 4: Se mejoró la redacción de la pregunta 4a), 4b), y 4d) y, a petición de una persona experta, que afirma la pregunta:
¿qué intervenciones realizaría usted como docente para superar dichas dificultades? debe tener una finalidad de enseñanza, por lo que se reemplazó por: ¿Conoces algún tipo de significado de la probabilidad que permita trabajar este problema?, ¿cómo lo implementarías para este problema? Finalmente, se incluyó 4c) en la categoría KoT y 4d) en las categorías KMLS y KSM.
Ítem 5: Se mejoró la redacción de 5a) 5b y 5c. Además, se añadió 5b) a las categorías KMLS y KSM y la pregunta 5c a la categoría KFLM.
Una vez refinado nuestro instrumento por medio de una reformulación, adecuación y selección definitiva de los ítems, en las Tablas 3 y 4 se muestra la vinculación de los ítems del cuestionario con el modelo MTSK que, desde el marco del EIEM, ha quedado distribuido de la siguiente manera:
Tabla 3 Vinculación definitiva, de los ítems del cuestionario MTSK-Estocástico de estadística con los subdominios del modelo MTSK y los contextos del EIEM
| Contextos /Subdominios | Reales | Materiales manipulables | Juegos | Recursos tecnológicos | Recursos gráficos |
|---|---|---|---|---|---|
| KoT | 1a) | 3a) | 4a) | 5b) | |
| KSM | 1a) y 1d) | 3a) y 3d) | 4a) | 5b) | |
| KPM | |||||
| KMT | 1c) | 2b) | 3c) | 4d) | 5d) |
| KFLM | 1b) | 2a) | 3a) y 3b) | 4a) y 4b) | 5a) y 5c) |
| KMLS | 1a), 1c) y 1d) | 2c) | 3d) y 3e) | 4c) | 5e) |
Nota: Fuente propia de la investigación.
Tabla 4 Vinculación definitiva, de los ítems del cuestionario MTSK-estocástico de probabilidad con los subdominios del modelo MTSK y los contextos del EIEM
| Contextos / Subdominios | Reales | Materiales manipulables | Juegos | Recursos tecnológicos | Recursos gráficos |
|---|---|---|---|---|---|
| KoT | 1a) | 2a) y 2b) | 3a) | 4a) y 4c) | |
| KSM | 2b) y 2e) | 4d) | 5b) | ||
| KPM | 1a) | 2a) | 3a) y 3c) | ||
| KMT | 1a) y 1c) | 2d) | 3c) | 4c) | 5c) |
| KFLM | 1b) | 2c) y 2d) | 3b) | 4b) | 5a) y 5c) |
| KMLS | 1d) | 2e) | 4d) | 5b) |
Nota: Fuente propia de la investigación.
Análisis y resultados
Aplicación piloto del cuestionario MTSK-estocástico
La aplicación piloto del cuestionario tiene como objetivo valorar distintos aspectos como: adecuación del tiempo estimado (90 minutos), claridad, compresión de enunciados e índice de dificultad. Con esta finalidad, se consideró una muestra de 4 docentes en activo que impartieran clases en el ciclo superior de Educación Primaria.
Se mandó un correo electrónico con las instrucciones claras y precisas sobre cómo responder el cuestionario y sobre el objetivo de la aplicación. Desde esta perspectiva, se realiza un análisis cualitativo fundamentado con las distintas aclaraciones de dificultades o argumentaciones de mejoras del instrumento. Tales dudas o propuestas se registraron permitiendo observar aspectos importantes para la mejora del instrumento. En este sentido, en términos generales, un grupo de docentes planteó la posibilidad de hacer el cuestionario a través de una plataforma online para facilitarles el trabajo a la hora de contestar las distintas cuestiones.
Además de realizar un análisis cualitativo, el cuestionario fue analizado cuantitativamente desde la perspectiva de dos variables: 1el grado de corrección de las respuestas al ítem, asignando valores 0 si la respuesta es incorrecta, 1 si es parcialmente correcta y 2 si es correcta; 2el índice de dificultad (ID), definida como la razón entre el número de aciertos y el número de respuestas (Muñiz, 2017). De esta forma, se asignaron valores entre 0 (alto grado de dificultad) y 1 (grado de máxima facilidad).
Ítems de estadística
En cuanto al grado de corrección de las respuestas, nadie del personal docente obtuvo la puntuación máxima (42), y las puntuaciones variaron entre los 15 y 30 puntos, siendo la media de 23,55, por lo que el porcentaje de logro fue del 64%.
En relación con el índice de dificultad sobre el cuestionario de estadística, clasificamos las respuestas en correctas e incorrectas. La Tabla 5 muestra un resumen estadístico de los datos.
Como se observa en la Tabla 5, el cuestionario presentó una dificultad media de un 36%. Los ítems de mayor dificultad fueron 1b,) 1c), 2a) y 4b) vinculados al KFLM, KMT y KMLS, KFLM, respectivamente.
A continuación, se describen los principales resultados para cada uno de los ítems.
Ítem 1
Este ítem se adapta a partir del cuestionario de Estrella, S. (2010) con la finalidad de evaluar el KoT, KSM, KMLS, KFLM y KMT vinculados a la comprensión del rango y la media aritmética y la moda.
En la Tabla 6 se observa que hubo un alto porcentaje de respuestas parcialmente correctas. Además, el ítem 1c) refleja dificultades por parte del profesorado para proponer intervenciones que ayuden a superar las dificultades del alumnado.
Tabla 5 Índice de dificultad de los ítems del cuestionario de estadística
| Ítem | 1 | 2 | 3 | 4 | 5 | ||||||||||||||||
| a | b | c | d | a | b | c | a | b | c | d | e | a | b | c | d | a | b | c | d | e | |
| ID (%) | 50 | 0 | 0 | 50 | 0 | 0 | 50 | 75 | 25 | 50 | 75 | 100 | 25 | 0 | 25 | 0 | 50 | 50 | 50 | 25 | 50 |
Nota: Fuente propia de la investigación.
Tabla 6 Frecuencia de respuestas otorgadas al ítem 1 (n=4)
| Respuestas | ||||
|---|---|---|---|---|
| Ítem 1 | Correctas Frecuencia | Parcialmente correctas Frecuencia | Incorrectas Frecuencia | No responde Frecuencia |
| a) | 2 | 2 | 0 | 0 |
| b) | 0 | 3 | 1 | 0 |
| c) | 0 | 2 | 2 | 0 |
| d) | 2 | 2 | 0 | 0 |
Nota: Fuente propia de la investigación.
La mitad del profesorado logró identificar correctamente los conceptos y propiedades matemáticas que debe poner en práctica el alumnado (KoT, KSM y KMLS) en la siguiente situación problemática: reconocer el precio medio de los pantalones en una tienda de ropa. Sin embargo, la otra mitad tuvo dificultades en identificar más de un concepto, por lo que reflejó dificultades para analizar y corregir las respuestas del alumnado.
En cuanto al KFLM, el profesorado presentó, en términos generales, posibles dificultades del alumnado para responder la tarea presentada. Por ejemplo, ''no entender el concepto de media”, ''que les faltan datos”, etc.
Desde este prisma, tan solo la mitad presenta un cierto grado de KMT, al proponer algunas estrategias didácticas, generales, que facilitarían la comprensión del rango, media y moda. Estas dificultades para aplicar los conceptos y procedimientos estadísticos, algunas investigaciones las atribuyen a la ausencia de formación por parte del profesorado (Batanero, Díaz, Contreras y Roa, 2013).
Finalmente, el profesorado obtuvo una buena puntuación sobre el KSM y KMLS al identificar los contenidos matemáticos que se relacionan en el problema.
Ítem 2
Este ítem se reformula a partir del cuestionario de Siswono et al. (2018). Su propósito es evaluar el KFLM, KMT y KMLS, vinculadas a la comprensión de la frecuencia absoluta y relativa. En la Tabla 7 se observa que el ítem presenta mayor complejidad es el 2a), sobre el KFLM, en el cual el profesorado debe identificar las posibles dificultades del alumnado para resolver el problema. En este sentido, el profesorado no puede prever los problemas del alumnado y, por tanto, proporcionar unas estrategias
de enseñanza adecuadas para subsanar los posibles obstáculos que pueda encontrar el
alumnado (KMT). Esto se ve reflejado en el ítem 2b), donde el profesorado proporciona algunas estrategias de enseñanza, pero estas no son concluyentes. Además, no señalaron qué tipo de material ni cómo lo utilizarían, lo que muestra un débil KMT.
Tabla 7 Frecuencia de respuestas otorgadas al ítem 2 (n=4)
| Respuestas | ||||
|---|---|---|---|---|
| Ítem 2 | Correctas Frecuencia | Parcialmente correctas Frecuencia | Incorrectas Frecuencia | No responde Frecuencia |
| a) | 0 | 2 | 2 | 0 |
| b) | 0 | 2 | 2 | 0 |
| c) | 2 | 1 | 1 | 0 |
Nota: Fuente propia de la investigación.
Ítem 3
El desarrollo de la actividad del ítem 3 ha sido de elaboración propia. El objetivo de este ítem es evaluar el KoT, KSM, KFLM, KSM y KMLS relacionados con la elaboración de gráficos simples, concretamente, el diagrama de barras, a partir de la realización de un juego.
Al observar la columna sobre el índice de dificultad de los subítems, se observa que el ítem en su totalidad presenta un nivel de dificultad bajo, por tanto, no debería presentar problemas en su resolución para el profesorado.
Como se observa en la Tabla 8, la mayoría del profesorado respondió correctamente al ítem 3, sobre todo las respuestas correctas se centran en los subítems: 3a) referido a los conceptos y propiedades matemáticas que deben usar el alumnado para dar una solución correcta; 3d) relacionado con la interpretación del nivel adecuado del problema planteado; y, 3e) relativo a los contenidos matemáticos involucrados en la resolución de la actividad.
En cambio, los subítems 3b) concerniente a las dificultades que puede presentar el alumnado y el 3c) sobre las estrategias para solucionar los distintos problemas de aprendizaje, comprenden el mayor número de respuestas incorrectas.
Tabla 8 Frecuencia de respuestas otorgadas al ítem 3 (n=4)
| Respuestas | ||||
|---|---|---|---|---|
| Ítem 3 | Correctas Frecuencia | Parcialmente correctas Frecuencia | Incorrectas Frecuencia | No responde Frecuencia |
| a) | 3 | 0 | 1 | 0 |
| b) | 1 | 1 | 2 | 0 |
| c) | 2 | 1 | 1 | 0 |
| d) | 3 | 0 | 1 | 0 |
| e) | 4 | 0 | 0 | 0 |
Nota: Fuente propia de la investigación.
Ítem 4
El ítem 4 se ha elaborado a partir de la reformulación del cuestionario Estrella et al. (2015). Su finalidad es evaluar el KoT, KFLM, KSM, KMLS y KMT relacionados con la elaboración de diagrama de barras con un recurso tecnológico.
Al observar la columna sobre el índice de dificultad de los subítems, vemos que el ítem en su totalidad presenta un nivel de dificultad medio-alto. En este sentido, los resultados extraídos en la Tabla 9 reflejan dificultades, por parte del profesorado, para responder correctamente las distintas cuestiones planteadas.
Como se observa en la Tabla 9, los subítems con mayor número de respuestas incorrectas son: 4b, referido a las dificultades o errores del alumnado para resolver el problema; 4c), la interpretación del nivel adecuado, donde un grupo de docentes argumentó que el nivel es para ciclo medio (3º y
Tabla 9 Frecuencia de respuestas otorgadas al ítem 4 (n=4)
| Respuestas | ||||
|---|---|---|---|---|
| Ítem 4 | Correctas Frecuencia | Parcialmente correctas Frecuencia | Incorrectas Frecuencia | No responde Frecuencia |
| a) | 1 | 2 | 1 | 0 |
| b) | 0 | 2 | 2 | 0 |
| c) | 1 | 1 | 2 | 0 |
| d) | 0 | 2 | 2 | 0 |
Nota: Fuente propia de la investigación.
4º); y, finalmente, en el ítem 4d), relacionado con propuestas de intervención para superar las dificultades del alumnado, la mayoría del profesorado no da propuestas concluyentes, tratan el tema de manera general. Por ejemplo, ''realizar explicaciones en pequeños grupos, clarificar conceptos que no quedan claros”. O, en algunos casos incorrectamente, por ejemplo, algunas de las respuestas son: ''practicar con el applet”, ''intentar explicar cómo contabilizar a los compañeros que tienen perro o gato”. En ningún caso, el profesorado da estrategias apoyándose con material manipulativo para entender la tabla estadística proporcionada por el profesorado.
Ítem 5
Este ítem ha sido de elaboración propia. Su objetivo es evaluar el KoT, KMT, KMLS, KFLM y KSM vinculados con el análisis crítico de las informaciones presentadas a través de los gráficos estadísticos.
Como se observa en la Tabla 10, más de la mitad del profesorado respondió correctamente al ítem 5. La mayoría de las respuestas correctas se centran en los ítems 5a), 5b) y 5e) vinculados al KFLM, KoT y KSM y KMLS, respectivamente. Desde esta perspectiva, los resultados muestran que poseen cierto nivel en estos conocimientos en relación con las variables, valores de gráficos estadísticos y calcular el rango de los datos generados a partir de una simulación. Por otro lado, un 25% del profesorado presentó limitaciones al identificar las dificultades del alumnado y su posterior intervención.
El análisis de las respuestas al cuestionario de estadística refleja un conocimiento bajo del profesorado en relación con el KFLM y KMT, donde la mayoría no identifica correctamente las posibles dificultades o errores que puede encontrarse el alumnado en el proceso de aprendizaje. En este sentido, del análisis se extrae que el personal docente ha obtenido poca formación al respecto, se echan en falta distintas estrategias para enseñar de manera eficaz.
Ítems de probabilidad
Respecto al grado de corrección de las respuestas, nadie del grupo de docentes obtuvo la puntuación máxima (38), y las puntuaciones variaron entre los 13 y 25 puntos, con una media de 20,25 y un porcentaje del 64,5 %.
Por lo que se refiere al índice de dificultad sobre el cuestionario de probabilidad, la Tabla 11 muestra un resumen estadístico de los datos:
Tabla 10 Frecuencia de respuestas otorgadas al ítem 5 (n=4)
| Respuestas | ||||
|---|---|---|---|---|
| Ítem 5 | Correctas Frecuencia | Parcialmente correctas Frecuencia | Incorrectas Frecuencia | No responde Frecuencia |
| a) | 2 | 2 | 0 | 0 |
| b) | 2 | 2 | 0 | 0 |
| c) | 2 | 1 | 1 | 0 |
| d) | 1 | 2 | 1 | 0 |
| e) | 2 | 2 | 0 | 0 |
Nota: Fuente propia de la investigación.
Tabla 11 Índice de dificultad de los ítems del cuestionario de estadística
| Ítem | 1 | 2 | 3 | 4 | 5 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | a | b | c | d | e | a | b | c | a | b | c | d | a | b | c | |
| ID (%) | 25 | 25 | 0 | 75 | 50 | 0 | 25 | 75 | 50 | 50 | 0 | 25 | 50 | 0 | 0 | 50 | 25 | 100 | 50 |
Nota: Fuente propia de la investigación.
Como se observa en la Tabla 11, el cuestionario presentó una dificultad media de un 35,5 %. Los ítems de mayor dificultad fueron 1c,) 2b), 3b) 4b) y 4c) vinculados al KMT, KoT y KSM, KFLM, KFLM, KoT y KMT, respectivamente.
A continuación, se describen los principales resultados para cada uno de los ítems.
Ítem 1
Este ítem ha sido elaborado a partir de la reformulación del cuestionario de Estrella (2010). Su objetivo es evaluar el KoT, KMT, KPM, KFLM y KMLS vinculados con estimaciones basadas en las experiencias sobre el resultado (posible, imposible, seguro, más o menos posible).
Como se observa en la Tabla 12, la mayoría de las respuestas correctas se centran en los ítems 1a) y 1d), relacionados con el KoT, KPM, KMT, y KMLS, respectivamente. Los resultados muestran un nivel medio de conocimiento sobre las estimaciones del resultado de las elecciones más posible que suceda. Además, el profesorado sabe distinguir que contenidos matemáticos se relacionan con el contenido involucrado. En cambio, en los ítems 1b) y 1c), el profesorado tiene dificultades en determinar qué errores u obstáculos tendrá el alumnado para argumentar la mejor predicción posible y, posteriormente, evidencia falta de recursos para dar estrategias para subsanar estas dificultades.
Finalmente, si analizamos el ítem 1 en su totalidad, vemos que presenta una disparidad que va de lo simple a lo complejo. Esto es interesante de mantener, pues el cuestionario debe presentar distintos grados de dificultad, a fin de discriminar los tipos y niveles de conocimientos sobre la enseñanza de la probabilidad por parte del profesorado.
Tabla 12 Frecuencia de respuestas otorgadas al ítem 1 (n=4)
| Respuestas | ||||
|---|---|---|---|---|
| Ítem 1 | Correctas Frecuencia | Parcialmente correctas Frecuencia | Incorrectas Frecuencia | No responde Frecuencia |
| a) | 1 | 3 | 0 | 0 |
| b) | 1 | 1 | 1 | 1 |
| c) | 0 | 3 | 0 | 1 |
| d) | 3 | 1 | 0 | 0 |
Nota: Fuente propia de la investigación.
Ítem 2
Este ítem ha sido adaptado a partir del cuestionario de Vásquez y Alsina (2015). Su objetivo es evaluar el KoT, KPM, KSM, KFLM, KMT y KMLS, relacionados con los sucesos posibles e imposibles.
En la Tabla 13, se observa cómo el profesorado ha demostrado tener un conocimiento adecuado del KMT y KFLM en relación con el cálculo y comparación de probabilidades de sucesos posibles e imposibles. En cambio, no
Tabla 13 Frecuencia de respuestas otorgadas al ítem 2 (n=4)
| Respuestas | ||||
|---|---|---|---|---|
| Ítem 2 | Correctas Frecuencia | Parcialmente correctas Frecuencia | Incorrectas Frecuencia | No responde Frecuencia |
| a) | 2 | 1 | 1 | 0 |
| b) | 0 | 2 | 1 | 1 |
| c) | 1 | 3 | 0 | 0 |
| d) | 3 | 0 | 0 | 1 |
| e) | 2 | 2 | 0 | 0 |
Nota: Fuente propia de la investigación.
logran reconocer que conceptos o propiedades matemáticas debe usar el alumnado para solucionar el problema planteado.
Finalmente, hemos decidido conservar el ítem 2 en su totalidad, pues consideramos que es un ítem con un índice de dificultad equilibrado que va de más a menos. No obstante, hemos realizado algunas modificaciones en su redacción.
Ítem 3
Este ítem ha sido de elaboración propia. Su objetivo es evaluar el KoT, KPM, KFLM y KMT, vinculados con la predicción de sucesos más probables en una carrera de caballos.
En la Tabla 14 se aprecian mayores dificultades en el ítem 3a) vinculado con las respuestas que deben aceptarse como correctas, donde una parte de docentes manifestó que: ''todos los caballos tienen las mismas posibilidades porque, en esta actividad solo actúa el azar''sin tener en cuenta el suceso más probable en el lanzamiento de dados (que salga un seis u ocho). Además, el ítem 3b) relacionado con las dificultades que pueda tener el alumnado para llegar a la solución, también presentó complejidades, al afirmar que ''el alumnado no tenga en cuenta que todo depende del azar.”
Finalmente, se ha decidido conservar el ítem 3, pues consideramos que es un ítem con mayor dificultad y ayuda a determinar, de una manera más eficaz, el conocimiento del profesorado en distintos contextos de aprendizaje.
Tabla 14 Frecuencia de respuestas otorgadas al ítem 3 (n=4)
| Respuestas | ||||
|---|---|---|---|---|
| Ítem 3 | Correctas Frecuencia | Parcialmente correctas Frecuencia | Incorrectas Frecuencia | No responde Frecuencia |
| a) | 2 | 0 | 2 | 0 |
| b) | 0 | 2 | 1 | 1 |
| c) | 1 | 2 | 0 | 1 |
Nota: Fuente propia de la investigación.
Ítem 4
Este ítem ha sido elaborado a partir de la reformulación del cuestionario Begg y Edwards (1999). Su objetivo es evaluar el KoT, KFLM, KMT, KMLS y KSM, referido al carácter aleatorio de distintas experiencias a partir de un recurso tecnológico.
En la Tabla 15 se observa que hubo un alto porcentaje de respuestas en blanco, sobre todo en el subítem c). De acuerdo con lo manifestado por el profesorado, se debe a que desconocían los distintos significados de la probabilidad.
Respecto al subítem 1b), referido al KFLM, el profesorado tuvo dificultades para identificar los posibles errores del alumnado sobre el carácter aleatorio de sucesos.
Tabla 15 Frecuencia de respuestas otorgadas al ítem 4 (n=4)
| Respuestas | ||||
|---|---|---|---|---|
| Ítem 4 | Correctas Frecuencia | Parcialmente correctas Frecuencia | Incorrectas Frecuencia | No responde Frecuencia |
| a) | 2 | 1 | 1 | 0 |
| b) | 0 | 1 | 2 | 1 |
| c) | 0 | 0 | 2 | 2 |
| d) | 2 | 0 | 1 | 1 |
Nota: Fuente propia de la investigación.
Finalmente, a partir de las frecuencias expuestas, se evidencia que los subítems de mayor dificultad son 4b) y 4c), sobre el KFLM, KoT y KMT, respectivamente. Mientras, el ítem que menor dificultad presenta es 1a), sobre el KoT. No obstante, si analizamos el ítem 1 en su totalidad, vemos que presenta un índice de dificultad media, por lo que podemos decir que muestra una buena discriminación. Además, algunos subítems permiten discriminar y analizar algunos subdominios del conocimiento en mayor profundidad, como es el caso del KoT. Con base en lo anterior, se decidió conservar el ítem 4.
Ítem 5
El ítem ha sido adaptado a partir de la reformulación del cuestionario Estrella et al. (2015). Su objetivo es evaluar el KFLM, KMLS, KSM y KMT vinculados al cálculo de la probabilidad de un suceso.
Como se observa en la Tabla 16, la mayoría de las respuestas correctas se centran en los ítems 5b) y 5c), vinculados con el KFLM, KMT y KFLM, respectivamente. Los resultados muestran un nivel alto de conocimiento sobre los estándares de aprendizaje adecuados para 5º y 6º de Primaria. Además, la mitad del profesorado propuso intervenciones adecuadas para resolver las dificultades del alumnado, utilizando material manipulativo. Por ejemplo, traer los dulces requeridos en la tabla y, realizar la actividad cooperativamente en clase.
Mientras que la otra mitad sugirió algunas intervenciones sin argumentar el motivo y, por tanto, sin ser concluyentes. En cambio, en el ítem 5a) el profesorado presenta dificultades para determinar qué errores u obstáculos tendrá el alumnado para calcular la probabilidad de sacar un dulce rojo.
Pese a que el índice de dificultad del ítem 5 es fácil, es necesario incluirlo para equilibrar los grados de dificultad de los ítems que componen el instrumento.
Conclusiones
En este artículo se ha descrito el proceso de diseño, construcción y validación del cuestionario MTSK-epistémico de estadística y probabilidad que evalúa los dominios y subdominios del MTSK (Carrillo et al., 2018) desde los contextos de aprendizaje del EIEM (Alsina, 2018, 2019, 2020a). Este propósito responde al hecho que las investigaciones sobre el conocimiento del profesorado de primaria, en activo, en la enseñanza de la estadística y la probabilidad son muy escasas.
En el proceso de diseño, construcción y validación de la versión inicial del cuestionario MTSK-estocástico, formado por 5 ítems de estadística y 5 ítems de probabilidad, destacan las etapas de vinculación del MTSK con el EIEM, la valoración del juicio experto y el análisis de la aplicación piloto, todo lo cual nos han permitido informar acerca de la validez y fiabilidad de los ítems para mejorar y elaborar la versión final del instrumento.
La validación a través del juicio experto ha dado lugar a la eliminación de dos subítems de probabilidad que incidían en aspectos similares y, por lo tanto, se han fusionado. Asimismo, se han modificado once subítems relacionados con la estadística y trece referidos a la probabilidad para que fueran más comprensibles, de acuerdo con el criterio del equipo revisor. Por otro lado, a partir de los resultados obtenidos en la aplicación piloto, se ha extraído una primera aproximación del conocimiento del profesorado en la enseñanza de la estadística y la probabilidad desde los subdominios del modelo MTSK. Desde esta perspectiva, la versión final del cuestionario MTSK-estocástico de estadística y probabilidad (Anexo 1 y 2) ha quedado constituida por 5 ítems de estadística correspondientes a los distintos contextos del EIEM que analizan diferentes subdominios del MTSK: reales (KoT, KSM, KMT, KFLM, KMLS, materiales manipulativos (KMT, KFLM, KMLS) , juegos (KoT, KSM, KMT, KFLM, KMLS), recursos tecnológicos (KoT, KSM, KMT, KFLM, KMLS) y recursos gráficos (KoT, KSM, KMT, KFLM, KMLS). Por lo que se refiere a los ítems de probabilidad (5): reales (KoT, KMT, KFLM, KMLS), materiales manipulables (KoT, KSM, KPM, KMT, KFLM, KMLS), juegos (KoT, KPM, KMT, KFLM), recursos tecnológicos (KoT, KSM, KMT, KFLM, KML) y recursos gráficos (KSM, KMT, KFLM, KMLS). Desde esta perspectiva, a primera instancia, el profesorado presenta un nivel medio bajo en las categorías de conocimiento del profesorado, sobre todo, en los subdominios asociados a las dificultades del alumnado y las distintas estrategias para subsanar sus posibles errores.
Consideramos que el cuestionario MTSK-estocástico puede ser una herramienta útil, tanto para indagar en el conocimiento especializado del profesorado como para fortalecer los procesos de enseñanza y aprendizaje de la estadística y probabilidad en Educación Primaria. En posteriores investigaciones, serán necesarios otros estudios para seguir refinando los indicadores y, a la vez, para consolidar su validez y fiabilidad interna, con el propósito de aportar información consistente que se pueda usar en los procesos de formación del profesorado en activo y, de este modo, contribuir a la mejora de las prácticas de enseñanza de la estadística y la probabilidad en Educación Primaria desde la perspectiva de los distintos contextos del EIEM.
Consentimiento informado
Los autores declaran que las personas participantes fueron informadas acerca de la investigación, aceptaron participar y firmaron un consentimiento voluntario.