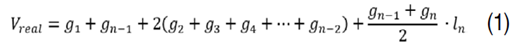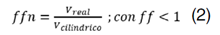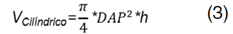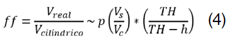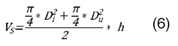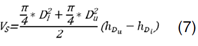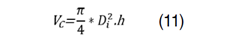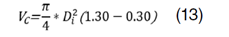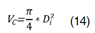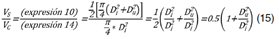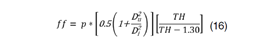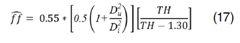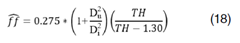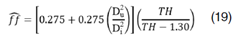Introducción
El volumen del árbol en pie es una de las fuentes de información más importantes para el conocimiento del potencial forestal y se considera como el mayor indicador del crecimiento forestal. Brinda información para comprender la productividad forestal y constituye la base para la planificación de actividades de manejo y aprovechamiento forestal (1), (2), (3). Es fundamental que su estimación sea precisa para tomar de decisiones certeras tanto en la planificación de la producción como su asignación para diferentes usos. Las estimaciones del volumen forestal a menudo dependen de la estimación del volumen de árboles individuales en función de las relaciones hipsométricas (4). La precisión de las estimaciones volumétricas se ve afectada por la variación en la forma del perfil del fuste (5). Esta se debe a la disminución natural del diámetro del árbol desde la base hasta la copa. La determinación del volumen por medio de características dendrométricas básicas como el diámetro a la altura del pecho (DAP) y la altura total (Ht) resulta en errores incrementados por factores como especie, procedencia, clima, edad y densidad (6). Esos factores ocasionan diferentes tasas de incremento del diámetro a diferentes alturas y determinan la forma del fuste.
La forma de los fustes no se identifica con la forma de un sólido geométrico específico, sino como un neiloide en la base, un paraboloide en el medio y un cono en la parte superior (7), (8). Si fuera posible determinar el principio y el final de cada figura geométrica a lo largo del eje, bastaría con aplicar las fórmulas geométricas correspondientes a los distintos sólidos geométricos que se presentan a lo largo del eje para obtener el volumen (9). Sin embargo, este proceso es prácticamente imposible, lo que motivó el desarrollo de métodos de corrección introducidos en la estimación de volúmenes de árboles en pie. Entre estos se destacan el cociente de forma, principalmente los de Girard, Schiffel y Johnson (10) y el factor de forma (1), (11), (12). Aunque este último suele ser más preciso, el desempeño de ambos depende de la estructura del tronco, habiendo reportes de que los cocientes estiman mejor las formas cónicas y neiloidicas, mientras que los coeficientes a los paraboloides (13). Las principales variantes del factor de forma son el factor de forma normal o artificial y el factor de forma de Hohenadl o natural (10).
El factor de forma es la relación entre el volumen real del árbol y el volumen de un sólido geométrico (cilindro) que tiene un diámetro igual al diámetro a la altura de pecho del árbol y una altura igual al del árbol (14), (15). Su uso reduce el error en la estimación del volumen (16), (17). Otras herramientas de estimación del volumen comercial de árboles son las ecuaciones volumétricas y los sistemas compatibles de ahusamiento y volumen comercial (18). Las ecuaciones volumétricas son más precisas que el factor de forma (19), pero este último es más utilizado hasta la fecha por su mayor practicidad y simplicidad de uso (20).
Para mejorar la precisión del factor de forma, (21) desarrollaron una expresión flexible generadora de factores de forma variables según la forma del árbol de especies del género Pinus. La funcionalidad de esta expresión depende de la correcta elección de la constante de proporcionalidad que no es más que el conocido factor de forma artificial. Por ello, el presente estudio se realizó con el objetivo de evaluar los desempeños del factor de forma artificial y el propuesto por (21) en la estimación de volúmenes de árboles de plantaciones de Eucalyptus spp. establecidas en Araripina, Pernambuco, Brasil.
Materiales y métodos
Ubicación y caracterización del área de estudio
El estudio se realizó en la estación experimental del Instituto Agronómico de Pernambuco (IPA), municipio de Araripina, región semiárida de Pernambuco, ubicada a una altitud de 831 m s.n.m. entre las coordenadas geográficas 07°27'37'' S y 40°24'36'' W, con Los suelos predominantes se clasifican como Latosol Amarillo y Latosol Rojo Amarillo (22). El clima es tropical semiárido con lluvias en verano y una precipitación media anual de 431.8 mm (23).
Caracterización del experimento
El experimento se implementó en marzo de 2002 en un área de 2.35 ha con 15 clones de Eucalyptus establecidos en parcelas de 21m×14m, en un espaciamiento de 3m×2m. Las parcelas experimentales están constituidas por 49 árboles, pero solo los 25 árboles del área útil se consideraron para el estudio.
Cubicación rigurosa
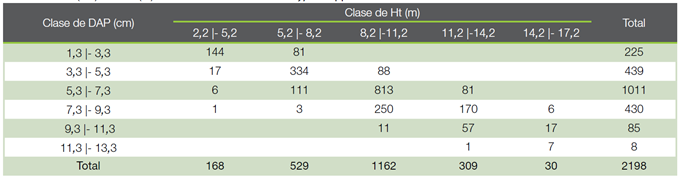
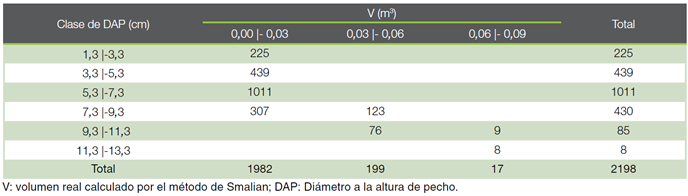
Los datos utilizados en este estudio provienen de la cubicación de 2198 árboles de Eucalyptus spp. Con ayuda de cintas diamétricas y forcípulas se midieron los diámetros a alturas de 0.3 m, 0.5 m, 0.7 m, 0.9 m, 1.10 m, 1.30 m (DAP), 1.50 m, 1.70 m, 2.30 m y a partir de esta se tomaron medidas a cada distancia de 1 m. La distribución de los árboles muestreados por clases de diámetro y altura y por clases de diámetro y volumen se muestran en los cuadros 1 y 2, respectivamente. La mayoría de los individuos medidos se distribuyen en las primeras cuatro clases de DAP (< 9.3 cm) y la primera clase de volumen (< 0.03).
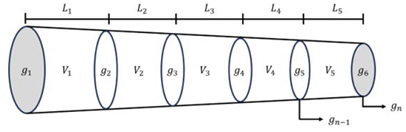
El volumen de cada árbol se determinó por el método de Smalian (Ecuación 1, Figura 1).
En que: 𝑉 𝑟𝑒𝑎𝑙 : volumen real del árbol; 𝑔₁ : área transversal 1; 𝑔 𝑛−1 : área transversal de la penúltima sección; 𝑔 𝑛−2 : área transversal de la antepenúltima sección; 𝑙 𝑛 : longitud de la última sección.
Figure 1. Illustrative image of log sectioning (Adapted from (24)).
El factor de forma normal (ffn) también conocido como factor de forma artificial fue calculado por la siguiente expresión (Ecuaciones 2 y 3, Figura 2).
En que: 𝑓𝑓𝑛: factor de forma normal o artificial; 𝑉 𝑟𝑒𝑎𝑙 : volumen real del tronco determinado por el método de Smalian; V Cilíndrico : volumen de cilindro con diámetro igual al DAP (diámetro medido a 1.30 m) y altura h; h: altura total.
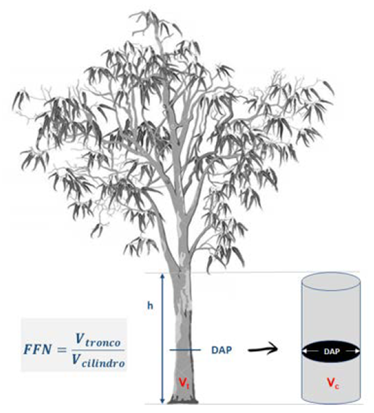
Figura 2 Determinación del factor de forma normal (ffn). Vtronco: volumen del tronco; Vcilindro: volumen de un cilindro de diámetro igual al DAP (Diámetro a la altura del pecho); h: altura comercial.
Figure 2. Estimation of the normal form factor (ffn). Vtronco: volume of the trunk; Vcilindro: volume of a cylinder of diameter equal to DBH (diameter at breast height); h: commercial height.
El factor de forma flexible propuesto por (21) es una aproximación del factor de forma normal y su expresión se muestra a continuación (Ecuación 4):
En que: p: constante de proporcionalidad; Di: diámetro medido a una altura de 0.30 m; Du: diámetro medido a una altura de 1.30 m; Vc: volumen del cilindro de diámetro Du y altura HDu - HDi = 1.30 m - 0.30 m; Vs : volumen de la sección primera entre Di y Du, estimado por el método de Smalian; TH : altura total; h : altura a la que el diámetro superior Du fue medido (1.30 m).
Determinando la expresión de Vs (Eq 4)
Vs Sustituyendo g=0.7854*D2 en la expresión 5, se tiene:
Considerando que ℎ = 𝐷 𝑢 − 𝐷 𝑖 , se tiene (Eq 6):
Sustituyendo ℎ 𝐷 𝑢 por 1.30 y ℎ 𝐷 𝑖 por 0.30 en la expresión 7, 8, 9 y 10, se tiene:
Determinando la expresión de Vc
Considerando h =h (Du )-h (Di ) se tiene eq 11:
Sustituyendo ℎ 𝐷 𝑢 por 1.30 y ℎ 𝐷 𝑖 por 0.30 en la expresión 12, se tiene:
Sustituyendo 15 en 4, se tiene eq 13, 14, 15 y 16:
Análisis de datos
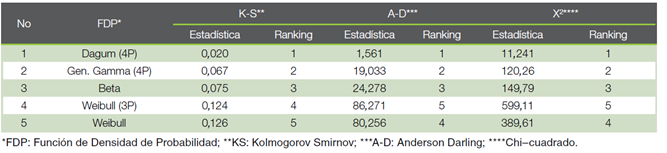
El éxito de este enfoque depende de la aproximación exacta de la constante de proporcionalidad p de la especie en cuestión, en este caso Eucalyptus spp. Por ello, se ajustaron funciones de densidad de probabilidad (Cuadro 3) para obtener la distribución y los valores más probables de la constante p para el Eucalyptus spp. La elección de la mejor función de distribución se realizó siguiendo los criterios de Kolmogorov-Smirnov (KS) y Anderson-Darling (AD).
Cuadro 3 Funciones de densidad de probabilidad ajustadas para la constante “p” en rodales de Eucalyptus spp. en el polo de producción de yeso de Araripe, Pernambuco, Brasil.

Se utilizó la prueba T de Student de muestras pareadas para comparar el volumen real de los árboles determinado por cubicación rigurosa (Smalian) con los volúmenes obtenidos a partir de los factores de forma generados por la variación de la constante de proporcionalidad en el enfoque de (21). El análisis de agrupamiento (línea Fenon trazada al 20% de disimilitud) y el de distribución de residuos se utilizaron para identificar los factores de forma con estimaciones volumétricas precisas y no sesgadas.
Resultados y Discusión
Factor de forma artificial
El factor de forma artificial tuvo un valor aproximado de 0.53, el cual está en consonancia con los valores reportados para Eucalyptus spp. en diferentes localidades de Brasil. Tal es el caso de (29) y (30) que reportaron para Eucalyptus urograndis, factores de forma de 0.52 y 0.54, respectivamente. Para Eucalyptus urophylla, (31) reportó un factor de forma de 0.51. Es importante resaltar que el factor de forma artificial es una característica fenotípica determinada por el genotipo y el ambiente (32) y no debe ser necesariamente igual en otras regiones. Los valores observados variaron entre 0.35 y 1.21, indicando que la forma de los fustes es predominantemente paraboloide y cónica.
Funciones de Densidad de Probabilidad para la constante de proporcionalidad “p” para Eucalyptus spp. en el polo yesero del Araripe
Las estimaciones de los parámetros de las funciones de densidad de probabilidad se encuentran en el Cuadro 4.
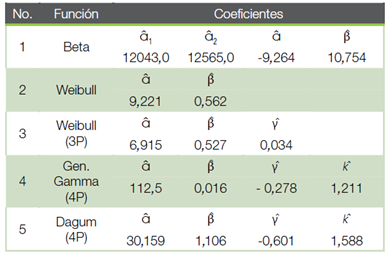
Cuadro 4 Estimativas de los parámetros de las Funciones de Densidad de Probabilidad ajustadas para la constante “p” para plantaciones de Eucalyptus spp. en el polo yesero del Araripe, Pernambuco, Brasil.
Cuadro 5 Bondad de ajuste de las Funciones de Densidad de Probabilidad ajustadas para la constante “p” para Eucalyptus spp. en el polo yesero del Araripe, Pernambuco, Brasil.
La Figura 3 presenta las distribuciones de las estimaciones del factor de forma artificial o constante de proporcionalidad (p) del enfoque de (21). Dado que los valores variaron entre 0.50 y 0.60 en la mayoría de las funciones, se consideraron 0.50, 0.55 y 0.60 como posibles constantes de proporcionalidad.
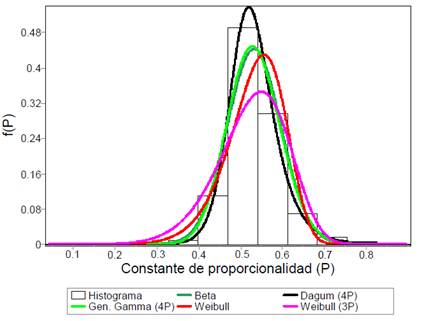
Figura 3 Funciones de Densidad de Probabilidad ajustadas para la constante “p” para Eucalyptus spp. en el polo yesero de Araripe, Pernambuco, Brasil.
Figure 3. Probability Density Functions adjusted to the constant "p" for Eucalyptus spp. in the Araripe gypsum pole, Pernambuco, Brazil.
Considerando la constante de proporcionalidad p = 0.55 y sustituyendo ese valor en la ecuación 16, se tiene eq 17, 18 y 19:
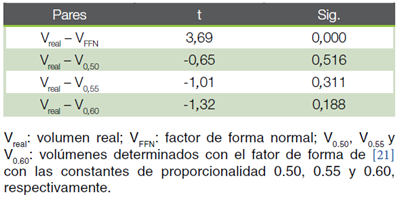
Con la ecuación 19 se estimó el factor de forma para determinar el volumen de cada árbol. El análisis de agrupamiento, con la línea Fenon al 20% de disimilitud (80% de similitud) identificó dos grupos (Figura 4). El primero está conformado por el volumen real (Vreal) y los estimados V0.50, V0.55 y V0.60. Eso indica que esas estimaciones tienen más de 80% de similaridad con los volúmenes reales de los árboles. Los volúmenes estimados con el factor de forma normal (VFFN) al ser menos similares a los volúmenes reales fueron clasificados en el segundo grupo. Fue confirmado por la prueba t pareada cuyos resultados indicaron que VFFN difirió significativamente de Vreal (Cuadro 6). Los volúmenes estimados con los factores de forma alternativos fueron estadísticamente similares a los volúmenes reales determinados por la cubicación rigurosa.
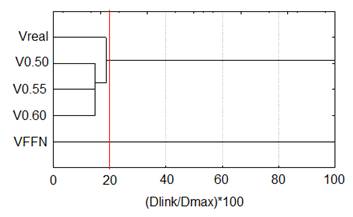
Figura 4 Análisis de agrupamiento del volumen real y los volúmenes estimados con los factores de forma.
Figure 4. Clustering analysis of the real volume and the volumes estimated with the form factors.
Los volúmenes determinados por los diferentes enfoques difirieron significativamente (F=22.54; GL=4; P<0.001). Con la constante p=0.50 y el factor de forma artificial (FFN=0.53), se obtuvieron estimaciones de volumen significativamente menores a los volúmenes reales (Figura 5). Los volúmenes determinados con la constante p=0.55 fueron similares a los volúmenes reales y los de p=0.60 fueron significativamente mayores que estos. Lo anterior indica que la constante p = 0.55 es la más indicada para Eucalyptus spp. en el peso yesero de Araripe.
Figure 5. Comparison of volumes estimated by the different approaches.
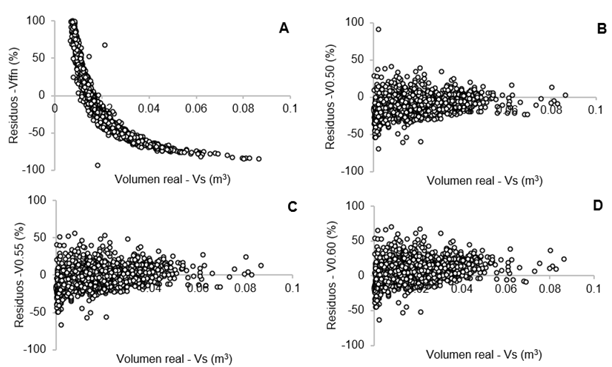
La distribución de residuos en la estimación del volumen de Eucalyptus spp. utilizando los diferentes factores de forma (Figura 6) fue un análisis complementario esencial para la elección definitiva del parámetro “p” a ser utilizado para la mejor estimación del volumen de los árboles utilizando el enfoque de (21).
Figure 6. Residual distributions of the volumes obtained with the form factors.
La distribución de residuos del factor de forma artificial revela sesgos en las estimaciones de volumen (Figura 6A). Se observa una clara tendencia de sobreestimar los valores más pequeños y subestimar los valores más grandes. Esto indica que el factor de forma artificial no capturó todo el componente determinista del volumen de cada árbol. Además de la especie, la forma del árbol es influenciada entre otros factores por el sitio, el espaciamiento, los tratamientos silviculturales y la edad. Por ello, se debe tener mucho cuidado al utilizar un único valor medio para representarla como lo hace el factor de forma artificial (10).
Por otra parte, los factores de forma alternativos (FF0.50, FF0.55 y FF0.60) tuvieron estimaciones volumétricas más precisas, sin sesgo y mantuvieron una varianza constante e independiente del tamaño del árbol (Figuras 6B, C y D). Eso se debe a la capacidad del factor de forma de (21) para aproximar la forma de cada árbol que puede ser casi cilindro, paraboloide, cono o neloide. La funcionalidad de ese fator de forma depende de una constante de proporcionalidad que no es más que una aproximación del factor de forma artificial. Para el género Pinus, considerando datos de Pinus taeda y Pinus elliottii en el sur de Estados Unidos y Pinus caribaea var. Hondurensis en Sri Lanka, la constante de proporcionalidad fue de 0.50 (21), contra 0.55 para Eucalyptus spp. en el nordeste de Brasil. A diferencia del factor de forma artificial que es un valor único utilizado para una especie (o grupo de especies), el factor de forma flexible es más específico al considerar variaciones a nivel de individuos, permitiendo reducir los errores de estimación tanto a nivel de árbol como de rodal.
Conclusiones
El factor de forma flexible (p=0.50) generó estimaciones no sesgadas y más precisas, comparado con las del factor de forma artificial cuyas estimaciones fueron menos precisas y sesgadas, principalmente para los volúmenes extremos.
Queda demostrado que el factor de forma flexible de Silva, Borders y Brister es funcional para especies de Eucalyptus spp. para las cuales supo captar el realismo de la forma de cada árbol y generó estimaciones de volumen consistentes.
Conociendo las dimensiones de la sección primera, la fórmula obtenida puede ser utilizada para estimar el volumen de árboles de Eucalyptus spp.