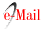Actualmente, se requiere información actualizada y disponible sobre la abundancia de las poblaciones para determinar los cambios a lo largo del tiempo o en el manejo de las poblaciones de cocodrílidos. La estimación de la densidad o abundancia de una población nos permite conocer y evaluar el estado de la misma en un área determinada, lo que permite saber el número de individuos y su distribución en el espacio (Ojasti & Dallmeier, 2000; Williams, Nichols & Conroy, 2002). Por ello, la abundancia se expresa en términos absolutos o tamaño de población (N=número de individuos en una población en un área definida) o densidad (D=número promedio de individuos por unidad de área), o mediante índices de abundancia (generalmente el número de animales o sus rastros detectados por el animal y por unidad de esfuerzo; Ojasti & Dallmeier, 2000).
La mayoría de los estudios estiman la abundancia de caimanes por el método convencional de recuentos visuales nocturnos, acompañados del marcado y recaptura de individuos, para estimar la estructura de edades de una población (Velasco & Ayarzaguena, 1995; Da Silveira, Magnusson, & Campos, 1997; Newell, 2001; Rebelo & Lugli, 2001; Ulloa-Delgado & Gavanzo-Ulloa, 2003; Cabrera, Urriola, & Cuberoet, 2003; Balanguera-Reina & Gonzáles-Mayas, 2009; Velasco & Ayarzaguena, 2010). Siendo la principal desventaja de los recuentos visuales nocturnos, el posible sesgo en la detección visual de individuos debido a variables físicas tales como: la cantidad de vegetación entre el observador y el animal, el ancho y la forma del río, lago o estuario, la sinuosidad del cuerpo del agua, la cantidad de canales secundarios, la posición del cocodrilo con respecto al observador, la intensidad del haz de luz y la frecuencia de los recorridos (Ron, Vallejo, & Asanza, 1998; García-Grajales, 2007).
En adición a lo anterior, los factores ambientales tales como la velocidad del viento, la lluvia, las fases de la luna, la niebla, el nivel del agua y la temperatura del aire y el agua pueden sesgar la detección de cocodrílidos en un hábitat (Pacheco, 1996; Llobet & Seijas, 2003; Da Silveira, Magnusson, & Thorbjarnarson, 2008; Aranda-Coello, 2016).
Utilizando una metodología apropiada, se pueden estimar los parámetros respectivos N y debido a que una población total de una especie en un momento dado (tamaño) y una densidad real, casi nunca se pueden determinar con precisión, debido a los “errores de medición” de la abundancia: algunos individuos estarán bajo el agua en el momento del conteo o no se detectarán de otra manera, lo que demuestra que los conteos crudos casi siempre representarán una subestimación del tamaño real de la población. Por lo tanto, surge la pregunta de ¿Qué tan “buenos” son estos estimadores? ¿En qué punto la estimación se acerca a los parámetros verdaderos? (Ojasti & Dallmeier, 2000).
Como resultado del posible sesgo en el método tradicional de estimar las proporciones de abundancia de cocodrílidos o el tamaño de la población, este estudio pretende estimar la abundancia de caimanes en el Refugio de Vida Silvestre Caño Negro por recuentos visuales tradicionales, utilizando una clase de modelos conocidos como N-Mixture (Royle, 2004; Fujisaki et al., 2011). Los modelos de "N-Mixture” combinan un modelo para recuentos imperfectos de una población con un modelo de variación espacial en tamaño de población latente entre "sitios" (unidades espaciales).
MATERIALES Y MÉTODOS
El Refugio de Vida Silvestre Caño Negro (RNVSCN) se encuentra en la zona noroeste de Costa Rica (10°48'12"-10°57'21"N & 84°42'30"-84°45'50"O), en la provincia de Alajuela, entre los cantones Chiles y Guatuso en el distrito de Caño Negro (Sáenz, 2001; Fig. 1). La zona es considerada un bosque tropical húmedo (Holdrige, 1947) y se caracteriza por un sistema de huecos estacionales que varían dependiendo de los cambios en el lecho del río Frio y sus afluentes. Tiene una estación seca que va de los meses de enero a abril y una estación lluviosa de mayo a diciembre (Cabrera et al., 2003).
Detección visual nocturna: de septiembre 2012 a agosto 2013, se llevó a cabo el muestreo visual nocturno en 21km del rio Frio (desde Betel hasta Boca Sabogal) en un bote con Motor fuera de borda (40HP), viajando a una velocidad aproximada de 10km/h. La ruta (21km de río) se dividieron en 32 segmentos de conteos (sitios) de 500m, con 200m de separación entre cada recuentro de segmento. En cada muestreo visual, dos observadores entrenados se ubicaron a cada lado del bote (derecha-izquierda) para contabilizar a los caimanes, utilizando linternas (Coleman 2 millones de lúmenes y conectado a una batería de 12 Mac550 v.). Los observadores contaban los caimanes por el destello de sus ojos de las 20:00 a 22:00hrs (tiempo que duraba el recorrido) en ±50m en cada lado (derecha-izquierda) de la ruta designada.
Modelo: se utilizó un modelo jerárquico binomial de Poisson, que se ha usado previamente para estimar el tamaño o la tendencia de la población a partir de datos replicados (Royle, 2004). El diseño del estudio considerado aquí es uno en el que los animales se cuentan durante t = 1, 2, ..., T ocasiones de muestreo (tiempo) y eni= 1, 2, ..., R ubicaciones (sitios). Dejando que Nit sea el número de individuos distintos contados en la ubicación i, en el tiempo t. de acuerdo con la siguiente ecuación (Royle, 2004):
n it ∼ Binomial (N i , p),
Donde Ni es el número de individuos disponibles para el muestreo (e.g. el tamaño de la población en el lugar i) y p es la probabilidad de detección (o captura). Las detecciones de animales se consideran independientes, y todos los animales presentes en un sitioien cualquier momento t, denotados Nit (abundancia de la población). Aunque en general p puede variar espacial y temporalmente, posiblemente en relación de las medidas covariables.
Es importante mencionar que la replicación espacial proporciona información adicional con respecto a los parámetros de la distribución previa de N (tamaño de población) explotada por los modelos de “N-mixture” y que puede conducir a estimaciones razonables de abundancia con datos dispersos cuando se obtienen recuentos duplicados en poblaciones cerradas (Royle, 2004). En los casos en que la abundancia específica del sitio no sea de interés directo (es decir, probablemente, en la mayoría de las situaciones), la expansión del área puede generar una estimación de la abundancia total. Esto puede ocurrir de varias maneras, dependiendo del contexto. Si las unidades de muestreo son de área conocida (por ejemplo, un recuento de radio de punto fijo), entonces es razonable estimar la abundancia total mediante una simple expansión del área sobre la base de la estimación de la densidad λ, bajo el supuesto de la distribución de Poisson, donde λ es la densidad por unidad (Royle, 2004).
Al mismo tiempo y con la intención de poder comparar la abundancia obtenida con el modelo N-mixture, realizamos el análisis con el método de Messel, Vorlicek, Wells y Green (1981). Este método tiene el supuesto que los ejemplares observados representan la fracción visible de la población, ya que existe cierto número que no fue posible observar porque se sumergieron antes de que el haz de luz hiciera contacto con sus ojos, y se calcula con la siguiente formula:
En donde p es el porcentaje de la población observada durante un muestreo promedio, m es un valor promedio de número de cocodrilos observados y s es la desviación estándar.
Una vez obtenido la fracción visible, es posible obtener el tamaño de la población (N) con un límite de confianza del 95%, de acuerdo con la siguiente ecuación:
Aunado a esto y con el propósito de comparar los resultados obtenidos con estudios anteriores se utilizó el método descrito por Chabreck (1966) para determinar la tasa de encuentro (TE) [número de individuos (ind.) / km lineal].
Ética, conflicto de intereses y declaración de financiamiento: el autor declara haber cumplido con todos los requisitos éticos y legales pertinentes, tanto durante el estudio como en el manuscrito; que no hay conflictos de interés de ningún tipo, y que todas las fuentes financieras se detallan plena y claramente en la sección de agradecimientos. Asimismo, está de acuerdo con la versión editada final del documento. El respectivo documento legal firmado se encuentra en los archivos de la revista.
RESULTADOS
La abundancia obtenida del modelo de "N-Mixture" para los 21km de río fue de 2 162 individuos con un error estándar (ES) ± 173,61, y un intervalo de confianza (IC) 95%: 1 847-2 531.
La abundancia estimada según el análisis tradicional, fracción visible de la población de Messel et al. (1981) produjo una abundancia estimada de 372,8 individuos con una desviación estándar (S) 61,05 con un IC: 95%: 366,13-379,47. Con respecto a la TE registrada fue de 99,85ind/km lineal.
DISCUSIÓN
El Refugio de Vida Silvestre Caño Negro es un área importante como hábitat para caimanes. Los resultados de la estimación de abundancia por el modelo “N-mixture” de Royle (2004), sugieren que el tamaño de la población fue mayor (2 162 individuos) que el método tradicional de Messel et al. (1981) basado en los conteos brutos, sin ningún tipo de error de detección (372,8 individuos). Esto se debe al hecho de que la visión nocturna depende mucho sobre la capacidad de identificar a todos los factores que influyen (e.g. cautela del organismo, distribución espacial entre otros) en lo visible de la fracción de muestreo (que finalmente es difícil; Ron et al., 1998).
Y dado que la mayoría de los estudios donde se estima la abundancia de caimanes tiene el método de recuentos visuales nocturnos, acompañados de captura-recaptura, (Velasco & Ayarzagüena, 1995; Da Silveira et al., 1997; Newell, 2001; Rebelo & Lugli, 2001; Ulloa-Delgado & Gavanzo-Ulloa , 2003; Cabrera et al., 2003; Balanguera-Reina & Gonzáles-Mayas, 2009; Velasco & Ayarzaguena, 2010, Tejado, 2012), demuestra que los conteos observados no se pueden equiparar con la abundancia verdadera, si no se tiene debidamente en cuenta el proceso de observación en el análisis de los datos de recuento de población, lo puede llevar a sobrestimar la verdadera variación en el proceso biológico (Link & Nichols, 1994) y a subestimar la abundancia (Schmidt, 2005).
Es por esto que la detección imperfecta es un problema típico de identificación de tendencias en la abundancia de la población que utiliza datos (Royle & Dorazio, 2006; Royle, Kéry, Gautier, & Schmid, 2007) por ello, la principal desventaja de los recuentos visuales nocturnos junto con sus análisis (Chabreck, 1966; Messel et al., 1981; King & Messel (in Cerrato, 1991)) podría ser por el posible sesgo en la detección visual de individuos, causada por la heterogeneidad espacial y temporal; aunque es una estimación conservadora, y por lo tanto, no es débil desde el punto de vista de la conservación, podría estar cayendo en un sesgo como lo menciona Fujisaki et al. (2011) que, en los programas de monitoreo a largo plazo que cubren múltiples ubicaciones, existen diferencias en la probabilidad de detección que puede ser atribuidas a la heterogeneidad espacial y temporal, lo que puede causar un sesgo en las estimaciones de abundancia.
Por lo tanto, un beneficio importante del modelo utilizado en el estudio, podría ser el ajuste en la probabilidad detección para el muestreo, ya que el modelo "N-Mixture" considera cada segmento de muestreo como respuestas temporales (con su propia probabilidad de detección), y de esa manera logra modelar el valor de la estimación (Royle, 2004). De acuerdo con lo mencionado por Fujisaki et al. (2011), el componente de abundancia de un modelo permite predecir cambios en el tamaño de la población simplemente como una función del tiempo, teniendo en cuenta los efectos confusos de los errores de detección.
Aunado a ello, la estimación de la abundancia con base en las TE de los caimanes ha sido la principal herramienta de estimación en Caño Negro, debido a que permiten realizar comparaciones entre estudios y sitios. Al comparar la TE promedio obtenida en este estudio en comparación con otros en el área (Cuadro 1), demostró ser superior. Lo que muestra que la población aumentó en los últimos años y es una de las altas tasas de encuentros registradas para los caimanes en el RNVSCN, y una de las más grandes registradas en el hábitat ribereño dentro de su área de distribución.
CUADRO 1: Tasa de encuentro de Caiman crocodilus en RNVSCN
| Referencia | Año | TE (ind/km lineal) |
|---|---|---|
| Allsteadt & Vaughan (1992) | 1989 | 53,0 |
| Junier (2000) | 1992 | 43,3 |
| Junier (2000) | 1993 | 26,6 |
| Junier (2000) | 1994 | 72,8 |
| Cabrera & Solano (1997) | 1997 | 58,7 |
| Cabrera et al. (2003) | 1999-2000 | 74,4 |
| Este estudio | 2012-2013 | 99,85 |
La principal ventaja de utilizar recuentos repetidos de unidades espaciales en el tiempo en segmentos de riberas y análisis basados en el modelo de “N-mixture”, en comparación con un índice basado en el valor máximo para el número de individuos observados, es que las estimaciones pueden interpretarse como estimaciones del tamaño de la población, lo que la convierte en una herramienta confiable para el posible manejo de la especie (Royle, 2004).
Las limitaciones potenciales del modelo de “N-mixture”. Por un lado, cuando los recuentos se realizan a lo largo del tiempo (días), las estimaciones son susceptibles de no cierre. Es decir, algunos individuos ya no están presentes en el segmento y es posible que algunos individuos nuevos se hayan trasladado a ese segmento. Esta emigración / inmigración tenderá a causar subestimación de p y, por lo tanto, sobreestimación de lambda. Una posible solución a esto es tener recuentos simultáneos duplicados de cada segmento. Por ejemplo, dos observadores en el mismo barco (que pueden reducir la sobreestimación de la población debido a la emigración / inmigración en el momento de los conteos nocturnos) o posiblemente muestras en estrecha proximidad temporal, como simple un tramo largo de la orilla del río y luego girar el bote alrededor y volver a muestrear los mismos segmentos casi de inmediato.
Y aunque el modelo de Royle (2004) no suele ser adecuado para simular datos de una población abierta, se realizó en este estudio para facilitar un examen de la velocidad a la que el modelo detecta la dinámica de la población y crear así una línea de base para comparación con la estimación de la abundancia obtenida por el método tradicional implementado en el estudio de caimanes. Por otra parte, el modelo de Royle (2004) puede ser aplicado a una población abierta si la población experimenta períodos de cierre conocidos (llamados primarios), durante los cuales se obtienen múltiples muestras (Royle & Dorazio, 2008 ; Kéry et al., 2009). Una situación llamada "diseño robusto" en la literatura para modelos de captura-recaptura (Pollock, 1982) y sitio (MacKenzie, Nichols, Hines, Knutson, & Franklin, 2003). Para esto, el modelo Royle (2004) ha sido probado por su bajo puntaje AIC y puede ser utilizado para poblaciones abiertas, ya que es más fácil de detectar la dinámica de la población para el modelo (Dail & Madsen, 2011).











 uBio
uBio