Introducción

Considerando que la “capacidad para resolver problemas es muy importante en matemáticas, no solo para aquellos que luego aprenderán o estudiarán matemáticas, sino también para aquellos que se integrarán en otros campos de la ciencia y en los valores de la vida cotidiana” (^{Masitoh, Nurdyansyah y Bachri, 2017}, p.258), el programa de matemática de la educación media costarricense (Ministerio de Educación Pública, 2012) aboga por una pedagogía de enseñanza y de aprendizaje de xla matemática basada en la resolución de problemas.

A razón de ello, analizar la medida en la que engrana la actitud hacia la matemática del estudiantado y la actitud hacia la resolución de problemas resulta relevante no solo por cuestiones formales, como lo es que la persona docente debe seguir los programas oficiales, sino porque de acuerdo con ^{Gil, Blanco, Gómez, Guerrero y Caballero (2015}) “La Resolución de Problemas ha sido considerada desde siempre como el foco en las matemáticas (…) como eje vertebrador del contenido matemático, ya que pone de manifiesto la capacidad de análisis, comprensión, razonamiento y aplicación” (p. 11).

El estudio cuyos resultados se reportan en este artículo, se enfocó en analizar la relación entre dos de las variables del denominado dominio afectivo en matemática, a saber, la actitud hacia la matemática y hacia la resolución de problemas, para indagar si existen diferencias en los niveles mostrados hacia estas por el estudiantado según sexo, nivel educativo o colegio.

\Dentro del estudio del dominio afectivo hacia la matemática, el punto de partida se encuentra en los trabajos de ^{McLeod (1992}). En años posteriores, el tema del domino afectivo ha ido cobrando particular relevancia dentro de la didáctica de las matemáticas, pues diversas investigaciones sobre las consecuencias de los factores afectivos en el aprendizaje reconocen que las emociones desarrolladas por el estudiantado podrían relacionarse con el aprendizaje que logran. En particular, ^{Auzmendi (1991}) señala que factores como la motivación, la ansiedad, el temor ante la materia, el agrado o el disfrute que provoca el trabajo matemático, la utilidad y el valor que el estudiantado le otorga a la disciplina para su vida profesional, y la confianza o el sentimiento que provoca la habilidad en matemática son elementos que forjan la actitud hacia la materia.

^{Gil, Blanco y Guerrero (2006}) destacan la importancia del domino afectivo hacia las matemáticas al indicar que, si una persona estudiante “manifiesta sentimientos positivos hacia la materia, estas actitudes condicionan que el estudiante obtenga mayor éxito académico que otro que ha desarrollado actitudes negativas” (p. 556). Por su parte, ^{Martínez (2008}) señala que “los referentes afectivos tales como las emociones, las creencias o las actitudes no representan algo suntuoso o artificial, sino que están comprometidos e involucrados con el éxito o con el fracaso de los estudiantes (…) y a la construcción de saberes matemáticos” (p. 247).

Dentro del marco del dominio afectivo en matemática, entra en juego una serie de categorías que modelan la opinión de las personas en cuanto al aprecio que se puede llegar a desarrollar para con esta disciplina. Tales categorías consideran diversos aspectos como las creencias, el gusto, la percepción o el autoconcepto matemático (^{Sánchez, 2013}).

Actitud Hacia La Matemática

De acuerdo con ^{Gil et al. (2006}), la actitud se define como una predisposición evaluativa (es decir, positiva o negativa) que determina las intenciones personales que influyen en el comportamiento.

Consta, por lo tanto, de tres componentes: una cognitiva, que se manifiesta en las creencias subyacentes en dicha actitud; una componente afectiva, que se manifiesta en los sentimientos de aceptación o de rechazo de la tarea o de la materia; y una intencional o de tendencia hacia cierto tipo de comportamiento. (p. 20)

Ahora bien, si el objeto es la matemática, se pueden distinguir dos grandes categorías: actitud matemática y actitud hacia las matemáticas. La primera considera las capacidades de los sujetos y su modo de utilizarlas en contextos diversos:

Dichas capacidades tienen que ver con la flexibilidad de pensamiento, apertura mental, el espíritu crítico, entre otros importantes para el trabajo matemático. Esta categoría es de carácter cognitivo, relacionado a la experiencia y sus logros antes que a lo afectivo. (^{McLeod, 1992}, p. 581

La actitud hacia la matemática se entiende como la valoración y el aprecio por esta disciplina, así como el interés y aprendizaje en términos de interés, satisfacción, curiosidad, valoración, etc. (Chacón, 2009 citado por ^{Gallegos, 2019}). Asimismo, ^{Gómez (2009}) amplía esta definición al relacionar la actitud hacia la matemática con factores como la estima y valoración e interés por utilizarla en situaciones diversas. Además, se acompaña de creencias y justificaciones que funcionan como un sistema de explicación, por lo tanto, la opinión del estudiantado, basada en sus creencias, desencadena actitudes hacia las matemáticas que condicionan su forma de actuar (Gamboa y Moreira, 2016).

La importancia del estudio de la actitud hacia la matemática estriba en que, de acuerdo con ^{Mato y Muñoz (2010}), “las dificultades tanto de aprendizaje como la enseñanza pueden estar relacionadas con las actitudes (…) una mala predisposición hacia la matemática no ayudará mucho en el rendimiento si antes no se intenta mejorar su actitud hacia la materia” (p. 29). Además, en que, tal como plantean ^{Gil, et al. (2006}), si el estudiantado manifiesta sentimientos positivos hacia la materia, tales actitudes condicionan que obtenga mayor éxito académico si se compara con quienes han desarrollado actitudes negativas.

La Resolución De Problemas

La expresión “resolución de problemas” acompaña diferentes concepciones sobre qué es la matemática, y por qué debemos enseñar matemática en general y resolución de problemas en particular. Desde esta perspectiva, la didáctica de la matemática con base en la resolución de problemas adopta distintas caracterizaciones que se deben considerar como parte de una enseñanza afectiva hacia la matemática. ^{Kilpatrick (1985}), referenciado en el trabajo de ^{Vilanova et al. (2001}), brinda una especial diferenciación de los contextos de resolución de problemas:

Resolver problemas como contexto: los problemas son utilizados como vehículos al servicio de otros objetivos curriculares, por lo cual juegan cinco roles principales:

Resolver problemas como habilidad: la resolución de problemas es frecuentemente vista como una de tantas habilidades a ser enseñadas en el curriculum. Esto es, resolver problemas no rutinarios es caracterizado como una habilidad de nivel superior, por ser adquirida luego de haber resuelto problemas rutinarios. Entonces, las técnicas de resolución de problemas son enseñadas como un contenido con problemas de práctica relacionados, para que las técnicas puedan ser dominadas (^{Vilanova et al. 2001}, p. 3).

Resolver problemas es “hacer matemática”: se relaciona la pedagogía y la epistemología de la matemática, los estudiantes tienen que adquirir el sentido de la matemática como una actividad; es decir, sus experiencias con la matemática deben ser consistentes con la forma en que la matemática es hecha (^{Vilanova, et al. 2001}, p. 4).

Se puede hablar de actitud hacia la resolución de problemas matemáticos al prestar atención a cómo el estudiantado afronta el “reto” de una situación problema de acuerdo con las definiciones anteriores. De hecho, algunas personas investigadoras consideran que el término “problema” desencadena en el estudiantado una serie de estados emocionales, que suelen jugar en contra y a favor de su afecto hacia la matemática. ^{Gil et al. (2006}) puntualizan que “la ansiedad que siente el alumno ante la resolución de problemas, su sensación de malestar, de frustración, de inseguridad, el bajo autoconcepto que experimenta y, que, frecuentemente, le impiden afrontar con éxito las tareas matemáticas” (p. 553). Además, consideran que las creencias del estudiantado y su integración con situaciones de resolución de problemas conducen a situaciones afectivas, pues cuando la instrucción en la clase es diferente a lo que el alumnado espera, experimenta una discrepancia entre sus expectativas y sus experiencias, probablemente como resultado de fuertes respuestas emocionales.

^{Bravo et al. (2018}) hacen señalamientos puntuales al explicar que los intentos realizados para enseñar a los alumnos estrategias generales de resolución de problemas no han tenido éxito, por lo cual, debemos diseñar programas de intervención que integren los aspectos emocionales dentro de un proceso de acción y reflexión matemática. ^{Mato y Muñoz (2010}) encontraron que la actitud hacia la matemática y el rendimiento académico, medido por la calificación final, tiene una correlación positiva y relativamente alta , es decir, a medida que la actitud es más positiva, el estudiantado logra mayores calificaciones.

^{Northatta (2011}) desarrolló un estudio sobre la relación entre la actitud hacia la resolución de problemas y los logros matemáticos, cuyos hallazgos mostraron que es significativa la actitud general en la resolución de problemas y el rendimiento en matemática. Esta investigación no detectó una relación significativa entre el género, la actitud hacia la resolución de problemas y los logros en matemática

A su vez, ^{Palomino (2018}) y ^{Acero (2019}) encontraron, en educación primaria, una relación significativa y directa entre la variable actitud hacia la matemática y actitud hacia la resolución de problemas aritméticos de enunciado verbal. Mientras, ^{Gallegos (2019}) detectó, en la educación secundaria, una relación tanto directa como significativa entre la actitud hacia la matemática y la resolución de problemas algebraicos.

^{Meza y Azofeifa (2011}) desarrollaron un estudio sobre la actitud hacia la matemática en estudiantes de undécimo año de colegios públicos del cantón central de la provincia de Cartago. Encontraron que el estudiantado presentaba una actitud positiva moderada en cuanto a si la matemática es una disciplina útil, necesaria, agradable, formativa y aplicable.

En una línea similar, ^{Campos y Mora (2015}) estudiaron el tema de la actitud hacia la resolución de problemas matemáticos en el tercer ciclo en tres colegios privados. Determinaron que el 73.3% de los estudiantes muestran una actitud negativa hacia la resolución de problemas matemáticos y solo un 26.7 % manifiesta una actitud positiva. Además, observaron que, en promedio, estudiantes de sétimo presentan niveles de actitud hacia la resolución de problemas más altos que los de estudiantes de octavo y noveno.

^{Meza, Suárez y Agüero (2015}), en una investigación sobre la actitud de estudiantes de la educación media costarricense ante la resolución de problemas en matemática, encontraron que aproximadamente el 20% del estudiantado mostró una actitud baja o muy baja hacia la resolución de problemas matemáticos, lo que se sumaba al hecho de que cerca del 50% tenía una actitud media. Todo esto se catalogó como un hallazgo negativo. Además, los resultados revelaron diferencias estadísticamente significativas en el nivel de actitud hacia la resolución de problemas matemáticos por sexo; los hombres presentaron niveles mayores, aunque con un tamaño del efecto bajo.

Por su parte, ^{Camacho y Picado (2015}) investigaron sobre la actitud hacia la resolución de problemas matemáticos en el ciclo diversificado de tres colegios privados. Sus hallazgos indican que aproximadamente un 52% de los estudiantes muestran una actitud muy buena o buena actitud hacia la resolución de problemas.

Por otro lado, diversos estudios destacan que las reacciones emocionales resultan de discrepancias en factores como el sexo, el nivel educativo o la institución educativa. Así, por ejemplo, ^{Castillo y Picado (2014}), ^{Meza et al (2015}), ^{Camacho y Picado (2015}), Meza, Suárez y Agüero (2017), Calderón y Guillén (2016), ^{Sanabria (2016}), ^{Coto (2018}), y encontraron datos estadísticos de diferencias en la variable ansiedad matemática entre estudiantes de sétimo con octavo y duodécimo, octavo con sétimo y noveno, noveno con octavo y duodécimo con sétimo. Mientras que ^{Corrales (2014}), Castillo y Picado (2014), Camacho y Picado (2015), Meza, Suárez, Agüero y Calderón (2016), Meza et al. (2017), Calderón y Guillén (2016), y ^{Martínez y Ramírez (2022}) hallaron diferencias en el nivel de ansiedad matemática según el sexo: los hombres tienden a presentar niveles menores que las mujeres.

La búsqueda de estudios similares llevados a cabo en Costa Rica, en los que se relacionen las variables “actitud hacia la matemática” y “actitud hacia la resolución de problemas matemáticos”, en bases de datos (Scopus, Web of Science, Redalyc, Scielo, EBSCO y Dialnet), repositorios institucionales (Kimuk, RepositorioTEC), metabuscadores (BASE y OpenDoar) y catálogos de universidades costarricenses (Universidad de Costa Rica, Instituto Tecnológico de Costa Rica, Universidad Nacional y Universidad Estatal a Distancia) no arrojó resultados. Por lo tanto, se puede considerar que esta investigación es pionera en esa pretensión y constituye un eslabón de un conjunto de estudios desarrollados en el Instituto Tecnológico de Costa Rica en el llamado “dominio afectivo” en el campo de la educación matemática.

Método

La investigación tiene un enfoque cuantitativo, con un diseño no experimental, de corte transversal y alcance correlacional. En esta sección se presentan las características de la muestra, los instrumentos de medición aplicados, el procedimiento para recabar los datos y una descripción de las técnicas estadísticas utilizadas.

Participantes

La muestra se conformó con 528 personas estudiantes, de una población de 2062 personas estudiantes matriculadas en el año 2022, mediante un diseño muestral simple aleatorio, estratificado según el colegio y los niveles educativos. La distribución de la muestra por sexo, colegio y nivel académico se presenta en la Tabla 1.

Tabla 1 Distribución de la muestra obtenida en el estudio, según sexo, colegio y nivel educativo 

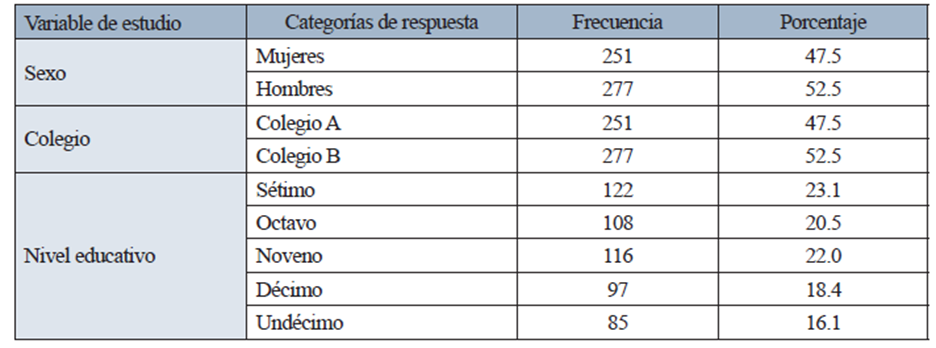
Fuente: elaboración propia

Variables

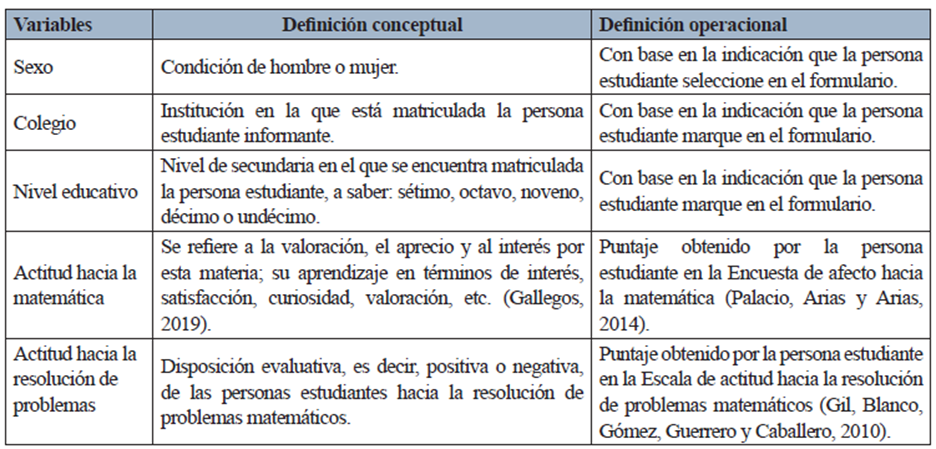
Las variables consideradas en la investigación son sexo, colegio, nivel educativo, actitud hacia la matemática y actitud hacia la resolución de problemas matemáticos, con las definiciones conceptuales y operativas de la Tabla 2.

Tabla 2 Definición conceptual y operativa de las variables 

Fuente: elaboración propia

Instrumentos de medición

Como instrumentos de medición se utilizaron la Escala de actitud hacia la matemática, diseñada y validada por ^{Palacios et al. (2014}), y la Escala de actitud hacia la Resolución de problemas”, validada por ^{Gil et al. (2010}). Ambas consisten en cuestionarios tipo Likert, constan de veinte ítems, con cinco posibilidades de respuesta desde “Totalmente de acuerdo” a “Totalmente en desacuerdo”, con la opción central de “No opino”.

Como parte del estudio de la validez, se calcularon los índices de discriminación de los ítems. Se obtuvo valores superiores a 0.3 en todos los casos de la escala “actitud hacia la matemática”, lo que indica una adecuada discriminación (^{Lozano y De la Fuente Solana, 2013}). Por su parte, de la escala “actitud hacia la resolución de problemas matemáticos”, de los análisis posteriores se eliminaron nueve de los veinte ítems que no alcanzaron el índice de baremación.

Además, se estudió el supuesto de unidimensionalidad de cada escala utilizando el análisis factorial, por ser la técnica más utilizada para estos propósitos (^{Jiménez y Montero, 2013}), con el cálculo previo del índice de Kaiser-Meyer-Olkin (KMO). Los valores KMO de 0.910 para “actitud hacia la matemática” y de 0.848 para “actitud hacia la resolución de problemas matemáticos” permiten considerar como excelente y buena la adecuación muestral, respectivamente, según la clasificación de Kaiser (1974), citado por ^{Frías y Pascual (2012}).

El índice de Bartlett de valor 0 para ambas escalas indica que es aceptable el uso del análisis factorial a los datos recabados. Por su parte, el análisis factorial produjo un primer factor que explica al menos el 36.072% de la varianza para la “actitud hacia la matemática” y un 34.825% de la varianza para la “actitud hacia la resolución de problemas matemáticos”, lo que evidencia la unidimensionalidad de cada escala de acuerdo con el criterio de Reckase (1979).

La confiabilidad de cada instrumento (la fiabilidad de la escala) fue estudiada mediante la técnica “Alfa de Cronbach”, utilizando como referencia el criterio de ^{Cea (1999}), el cual establece que un valor igual o superior a 0.8 indica una confiabilidad apropiada. Para la primera escala, se obtuvo un valor de 0.904 y para la segunda escala, un valor de 0.811, por lo tanto, ambas mostraron una adecuada confiabilidad.

Procedimiento

Los instrumentos se aplicaron al estudiantado de las secciones escogidas al azar, mediante la técnica de “papel y lápiz”, se integraron ambas escalas en un solo documento.

Análisis estadístico

El análisis estadístico descriptivo de los datos incluye la baremación de los puntajes para cada una de las escalas en las categorías baja y alta, según el puntaje fuera inferior o superior, respectivamente, al valor medio de la escala. Además, se sometieron a contraste las siguientes hipótesis:

Para la prueba de las hipótesis se utilizaron métodos paramétricos (T-Student o ANOVA, según correspondiera) y se asumió la normalidad de los datos con base en el teorema del límite central, debido a que cada categoría involucrada contiene aproximadamente 100 datos (^{Aguayo, 2004}).

Cuando se detectaron diferencias entre las medias de alguna de las dos variables en alguna de las categorías en contraste, se calcularon los tamaños del efecto, mediante el cálculo del coeficiente d de Cohen, cuya interpretación se realizó siguiendo las recomendaciones de Cohen: cerca de 0.2 es una diferencia pequeña; cerca de 0.5, moderada y superior a 0.8, grande (^{Morales-Vallejo, 2012})

Finalmente, para estudiar la existencia de correlación entre las variables “predisposición desfavorable hacia la matemática” y “autoconfianza matemática”, se aplicó el coeficiente de correlación de Pearson, previa prueba de hipótesis de que este coeficiente no era nulo.

Resultados

Clasificación del nivel de “Actitud hacia la matemática” y el nivel de “Actitud hacia la resolución de problemas matemáticos”

El valor medio de la escala de la “actitud hacia la matemática” corresponde a 60. La media de esta variable para la muestra (M = 66.38, SD = 14.219) resultó significativamente mayor que el valor promedio de la escala (t (527) = 107.277, p < 0.05), lo cual, interpretado de manera global, indica que el estudiantado muestra un nivel de “actitud hacia la matemática” superior al valor promedio; esto es, presenta niveles altos en esta variable.

Por otro lado, el valor medio de la escala “actitud hacia la resolución de problemas matemáticos”, con los ítems indicados en la Tabla 13 corresponde a 33. El valor medio de esta variable para la muestra (M=39.862, SD=7.192) resultó significativamente mayor que el valor promedio de la escala (t (527) = 127.362, p < 0.05). De manera global, este resultado indica que el estudiantado presenta un nivel de “Actitud RPM” superior al valor promedio, es decir, los niveles son altos para esta variable

Se clasifican los niveles de “actitud hacia la matemática” y de “actitud hacia la resolución de problemas” en dos categorías: positiva o negativa, según el puntaje sea menor o mayor, respectivamente, al valor medio de la escala correspondiente. Los resultados se presentan en la Tabla 3.

Tabla 3 Clasificación del nivel de “actitud hacia la matemática” y de “actitud hacia la resolución de problemas matemáticos” 

Fuente: elaboración propia

Contraste de la hipótesis 1

Para el contraste de la primera hipótesis, se comparó la media de las mujeres (M = 64.49, SD = 14.20) con la media de los hombres (M = 68.09, SD = 14.03) y se encontró una diferencia estadísticamente significativa (t (526) = -2.932, p = 0 <0.05, d=0.127). Por ello, se rechaza la hipótesis nula y se acoge la alternativa, lo que conlleva a aceptar la existencia de diferencias en el nivel de “actitud hacia la matemática” según el sexo, con media superior para los hombres y un tamaño del efecto (d = 0.127) que permite interpretar la diferencia como pequeña.

Contraste de la hipótesis 2

Para el contraste de la segunda hipótesis, se comparó la media de las mujeres (M = 38.97, SD = 7.31) con la de los hombres (M = 40,66, SD = 6.99), y se obtuvo una diferencia estadísticamente significativa (t (526) = -2.722, p = 0 <0.05, d=0.1185). Por tanto, se rechaza la hipótesis nula y se acoge la alternativa, es decir, se acepta la existencia de diferencias en el nivel de “actitud hacia la resolución de problemas matemáticos” según el sexo, con media superior para los hombres y un tamaño del efecto (d = 0.1185) que permite interpretar la diferencia como pequeña.

Contraste de la hipótesis 3

Para el estudio de la tercera hipótesis, se comparó la media de los cinco niveles educativos, aplicando la prueba ANOVA. La prueba de Levene (p = 0.074 > 0.05) permitió asumir la igualdad de varianzas y se determinó que existen diferencias, estadísticamente significativas, entre al menos un par de medias de los cinco niveles (F (4) = 3.853, p = 0.04 < 0.05).

Se utilizó la prueba post hoc de Bonferroni para comparar los diferentes pares de medias y se encontró que la del estudiantado de sétimo (M7 = 67.86, SD7 = 14.33, p < 0.05) es significativamente menor que la de décimo (M10 = 61.71, SD10 = 14.49, p < 0.05), con un tamaño del efecto bajo (d=0.06) y que la de noveno (M9=68.76,SD9=12.44,p<0.05), con un tamaño del efecto mediano (d=0.42).

Lo anterior señala diferencias estadísticamente significativas en el nivel de “Actitud hacia la matemática” entre el estudiantado del sétimo en comparación con el de décimo y el de noveno, con tamaño del efecto (d=0.06) bajo en el primer caso y moderado (d=0.42) en el segundo.

Contraste de la hipótesis 4

Para el estudio de la cuarta hipótesis, también se aplicó la prueba ANOVA para comparar la media de los cinco niveles educativos. La prueba de Levene (p = 0.443 > 0.05) permitió asumir la igualdad de varianzas y se determinó que no existen diferencias, estadísticamente significativas, entre al menos un par de medias de los cinco niveles (F (4) = 2.202, p = 0.068 > 0.05). Por lo tanto, no se detectaron diferencias en el nivel de “actitud hacia la resolución de problemas matemáticos” según el nivel educativo que cursa el estudiantado.

Contraste de la hipótesis 5

Para el contraste de la quinta hipótesis, se comparó la media del colegio A (M = 66.51, SD = 13.69) con la del colegio B (M = 66.26, SD = 14.7) y no se detectan diferencias estadísticamente significativas (t (526) = 0.196, p = 0.845 >0.05). Por ello, se acepta la hipótesis nula y se rechaza la alternativa, lo cual indica que no se detectaron diferencias en el nivel de “actitud hacia la matemática” según el colegio.

Contraste de la hipótesis 6

Para el estudio de la sexta hipótesis, se comparó la media del colegio A (M = 40, SD = 7.16) con la media del colegio B (M = 39.73, SD = 7.22) y no se detectan diferencias estadísticamente significativas (t (526) = 0.432, p = 0.666 >0.05). En consecuencia, se admite la hipótesis nula y se rechaza la alternativa, esto apunta que no se encontraron diferencias en el nivel de “actitud hacia la resolución de problemas matemáticos” según el colegio.

Contraste de la hipótesis 7

Para el contraste de la sétima hipótesis, se utilizó el coeficiente de correlación de Pearson entre las variables “actitud hacia la matemática” y “actitud hacia la resolución de problemas matemáticos”, y se encontró una correlación estadísticamente significativa entre ambas variables (r (528) =0.643, p=0). Es decir, se rechaza la hipótesis nula y se acepta que existe relación positiva, significativa y directa entre estas variables.

Discusión De Resultados

La investigación se enfocó en estudiar la relación entre las variables “actitud hacia la matemática” y “actitud hacia la resolución de problemas matemáticos” en dos poblaciones estudiantiles distintas de secundaria, con el fin de determinar si hay diferencias según sexo, nivel educativo y colegio. Los resultados obtenidos permiten visualizar que 65.9% del estudiantado presenta una actitud positiva hacia la matemática y 80.1% una actitud positiva hacia la resolución de problemas matemáticos, lo cual se comprueba con que el valor medio de estas variables en la muestra es significativamente superior al valor medio de la escala.

Los resultados para la variable “actitud hacia la matemática” coinciden con los de ^{Meza y Azofeifa (2011}), en los que el estudiantado manifestó una actitud positiva hacia la matemática en 78.5%. Por su parte, los resultados de la variable “Actitud hacia la resolución de problemas matemáticos” son más positivos que los obtenidos por ^{Camacho y Picado (2015}), donde aproximadamente 52% de las personas estudiantes muestran una muy buena actitud o buena actitud hacia la resolución de problemas y que los de Meza et al. (2015), en los cuales cerca del 50% tenía una actitud media. También, resultan más positivos que los encontrados por ^{Gil et al. (2006}), en los que el 51.7% de las personas estudiantes indicaban que les interesa o atrae la resolución de problemas matemáticos.

Por otro lado, para ambas variables de la investigación, se encontró que los hombres muestran valores en promedio más altos que las mujeres. Esto significa que existen diferencias en el nivel de “Atitud hacia la matemática” y “Actitud hacia la resolución de problemas matemáticos”, según el sexo. Este aspecto concuerda con otras investigaciones en el ámbito afectivo hacia la matemática y la resolución de problemas, donde los niveles, en promedio, son más altos para los varones (^{Gil et al., 2006}; ^{Corrales, 2014}; ^{Castillo y Picado, 2014}; ^{Camacho y Picado, 2015}; ^{Meza et al., 2016}; Meza et al., 2017; Calderón y Guillén, 2016; y ^{Martínez y Ramírez, 2022}).

Tales diferencias en las variables del domino afectivo según el sexo se suelen explicar por la presencia de estereotipos culturales acerca de la matemática, así como por el papel que juegan en el contexto matemático los hombres y las mujeres. Existe cierta predominancia de la idea de que las mujeres tienen menor rendimiento en tareas matemáticas en relación con los hombres, pero la evidencia indica que no hay razón alguna para suponer que rindan menos que ellos en este campo de estudio (^{Farfán y Ramos, 2013}; Bian, Leslie y Cimpian , 2017; Eccles (1987), citado por ^{Rodríguez, 2011}; ^{Nurlu, 2017}; y el Servicio de Información de Noticias Científicas (2010), citado por ^{León y Salazar, 2014}). Esta situación es importante, en especial en un país como Costa Rica, donde se aspira a que más mujeres opten por carreras STEM (ciencias, tecnología, ingeniería y matemática), porque, tal como señalan Farfán y Ramos (2013), refiriéndose a la matemática, si bien las mujeres no están en desventaja académica con los hombres, diversas situaciones del entorno las llevan a desestimar sus habilidades y a desistir de elegir carreras relacionadas con esta área.

A su vez, aunque se detectaron diferencias en esas variables según el sexo, los tamaños del efecto resultaron pequeños. Esto se puede interpretar, en términos prácticos, como que no es necesario diferenciar las acciones que emprendan las instituciones para mejorar los niveles en estas variables según el sexo de las personas estudiantes; por lo tanto, se puede considerar que las acciones de intervención educativa no tienen por qué ser diferentes para mujeres y hombres.

Asimismo, no se encontraron diferencias significativas para ambas variables según el colegio, lo que concuerda con los hallazgos de otras investigaciones realizadas en el ámbito costarricense en educación secundaria oficial diurna (^{Meza et al., 2016}; Meza et al., 2017; Calderón y Guillén, 2016; ^{Campos y Mora, 2015}; y ^{Martínez y Ramírez, 2022}). Pero contrastan con los resultados de ^{Ramos (2015}), así como con los hallazgos de Calderón y Guillén (2016). Ahora bien, aunque es cierto que en la mayoría de las investigaciones en el dominio afectivo los resultados suelen ser menos favorables para las mujeres que para los hombres, esta situación no se presenta en todos los casos. Por ello, tal como plantea ^{Mella (2006}), la diferencia entre hombres y mujeres en sus resultados en matemáticas es discutible desde todo punto de vista; basta con mencionar que, en los países europeos, en las mediciones hechas por la Organización para la Cooperación y el Desarrollo Económicos (OECD), las diferencias no son estadísticamente significativas o incluso las mujeres son las que están obteniendo mejores resultados en matemáticas. Por esto, no es de extrañar que los resultados de la presente investigación no concuerden con los de Ramos (2015).

Con respecto a la “actitud hacia la matemática” según el nivel educativo, se detectaron diferencias entre los niveles de sétimo y noveno, y entre sétimo y décimo. Aunque no en todas las investigaciones realizadas en el país en el dominio afectivo hay diferencias entre esos niveles, se han encontrado diferencias por nivel educativo en diversos estudios (^{Castillo y Picado, 2014}; ^{Meza et al., 2015}; Meza et al., 2017; Calderón y Guillén, 2016; ^{Sanabria, 2016}; ^{Coto, 2018}; y Camacho y Guzmán, 2020). Esto significa que en el estudio de las variables de dicho dominio es relevante considerar siempre el nivel educativo en que se ubica el estudiantado.

Sin embargo, en la variable “actitud hacia la resolución de problemas matemáticos”, según nivel educativo no se presentaron diferencias significativas, lo que concuerda con las investigaciones de ^{Camacho y Picado (2015}), así como con las de ^{Campos y Mora (2015}), quienes tampoco encontraron diferencias en algunas de las variables estudiadas. No obstante, el resultado es discordante con los datos obtenidos por ^{Meza et al. (2015}), los cuales señalan mejor actitud en los estudiantes de tercer ciclo que en los de la educación diversificada.

Para finalizar, en cuanto a la relación entre actitud hacia la matemática y actitud hacia la resolución de problemas, se presenta un índice de correlación positivo, significativo y directo. Esto permite inferir que el estudiantado con una actitud positiva hacia la matemática presenta, en términos generales, una actitud favorable hacia la resolución de problemas. Además, en un sentido recíproco:

una actitud positiva hacia la resolución de problemas favorece una visión positiva de la matemática.

Aunque la investigación no es de tipo explicativa, por ende, no se puede inferir una relación causal entre estas dos variables, los resultados permiten señalar evidencia estadística para sustentar una correlación entre la actitud que los estudiantes tienen hacia la matemática y su disposición de abordar la resolución de problemas matemáticos. En otras palabras, una visión positiva de la matemática (creencias, emociones, motivación) parece tener una afectación directa en la opinión del estudiante cuando se enfrenta a una metodología de aprendizaje basada en la resolución de problemas matemáticos. Al mismo tiempo, una enseñanza matemática con base en la resolución de problemas parece afectar de forma positiva la actitud de la persona estudiante sobre la matemática, esto concuerdan con los resultados a nivel internacional (^{Northatta, 2011}; ^{Palomino, 2018}; ^{Gallegos, 2019}; y ^{Acero, 2019}).

Si se considera que los programas vigentes, aprobados por el Consejo Superior de Educación en el año 2012, contemplan la “resolución de problemas” como metodología principal, cabe afirmar que los resultados de esta investigación son de relevancia y utilidad para el fortalecimiento de la enseñanza de la matemática en la educación secundaria costarricense, así como para motivar al profesorado de matemática de ese nivel a desarrollar investigaciones similares