Introducción
La reducción de las pérdidas de rendimiento de los cultivos debidas a enfermedades es abordada por el concepto de manejo integrado, el mínimo impacto ambiental y el máximo beneficio económico (Lavilla & Ivancovich, 2021). Para ello, se incorporan elementos como umbrales de daño económico, monitoreo y sistemas de pronóstico de riesgo, los cuales constituyen herramientas valiosas para definir estrategias de manejo y control de las enfermedades. El manejo integrado de enfermedades es una estrategia dinámica que debe generar soluciones en sistemas productivos cambiantes, por acción de la naturaleza o del hombre (March et al., 2010).
La interacción simultánea o sincrónica entre hospedante, patógeno y ambiente, gobierna el desarrollo de una enfermedad, que puede causar alteraciones fisiológicas y morfológicas en las plantas hospedantes. En la naturaleza, el llamado triángulo de la enfermedad, resulta de la acción combinada de un patógeno virulento, un hospedante susceptible y un ambiente favorable (Lavilla et al., 2022). Este patosistema interactivo se modifica cuando el hombre incorpora cultivos, con sus prácticas de manejo y estrategias de control de enfermedades.
La información agrometeorológica es fundamental para la predicción de brotes de enfermedades para el uso eficaz y responsable de las medidas de control, la predicción de los rendimientos de los cultivos y del potencial de mercado para el cultivo. Los principales factores meteorológicos responsables de los brotes de fitoenfermedades son la temperatura (tanto del aire como del suelo), la precipitación (lluvia y rocío), la humedad (humedad relativa, humedad del suelo), la radiación solar (intensidad y nubosidad), el viento, entre otros. Entre estas variables, la temperatura y la humedad se consideran como los factores más importantes, ya que todos los patógenos tienen un rango de requerimiento de temperatura y humedad óptimo para su crecimiento (Agrios, 2005).
Los modelos matemáticos y estadísticos permiten representar lo que sucede en los cultivos frente a distintos patógenos y en diferentes condiciones ambientales. En general, se utilizan dos estrategias para el modelado de datos efitiológicos: los modelos empíricos y los mecanísticos. La forma de describir el progreso epifítico, es a través de la relación observada entre dos o más variables, basándose en algunos o todos los factores capaces de expresar la enfermedad (Bombelli, 2011).
Si bien existen diversos métodos para la asociación de las variables meteorológicas con la severidad (SEV) de las enfermedades, el método de regresión logística no requiere el supuesto de normalidad multivariada para que sea válido (Henderson et al., 2007). Esto significa que, aun cuando los datos recopilados de incidencia y SEV no sean normales, igual pueden analizarse y generar un modelo predictivo de la enfermedad.
En Argentina, el cultivo de soja es la principal oleaginosa implantada en el país, con una superficie sembrada cercana a los veinte millones de hectáreas y una producción de 56 millones de toneladas (Lavilla et al., 2022). Entre las enfermedades del follaje, el tizón foliar por Cercospora (TFC) causado por Cercospora kikuchii es una enfermedad endémica en el cultivo de soja para el norte de la provincia de Buenos Aires (Lavilla et al., 2021). El TFC cuando no se controla en tiempo y forma sobre el cultivo de soja, puede causar pérdidas de rendimiento de hasta un 11 % (Lavilla & Ivancovich, 2021). Dentro del manejo integrado de enfermedades, es importante contar con un modelo predictivo y de esta manera poder anticiparce a posibles problemas sanitarios en los cultivo.
El objetivo de este trabajo fue desarrollar un modelo predictivo de la severidad del tizón foliar por Cercospora (TFC), mediante variables meteorológicas para el norte de la provincia de Buenos Aires, Argentina.
Materiales y métodos
Severidad del tizón foliar por Cercospora a campo
Se contó con datos de incidencia y severidad del tizón foliar por Cercospora (TFC) correspondiente a cinco ciclos productivos de soja (Glycine max) (2013-2017) de Pergamino, provincia de Buenos Aires, Argentina, relevados en distintos estados reproductivos (ER=R1 a R7) (Fehr et al., 1971) (Cuadro 1). Los datos fueron obtenidos de cincuenta lotes de soja por año de evaluación, ubicados entre las coordenadas S 33° 35' 46.752'y O 60° 44' 26.375'' y S 34° 11' 18.168''y O 60° 42' 15.552''. A partir de estos datos, se calculó la tasa de incremento (TI; %/día) como la diferencia entre la severidad medida en un estado reproductivo, menos la severidad medida en el estado reproductivo precedente, dividido entre el número de días transcurridos entre las dos mediciones (Moschini et al., 2006). Se optó por el valor de severidad para el cálculo de TI, debido a que la inclusión de la incidencia no influyó en el resultado final del modelo predictivo y en la selección de las variables climáticas relacionadas con la enfermedad. La escala utilizada para evaluar la severidad del TFC fue la de Lavilla et al. (2021).
Cuadro 1 Valores observados por año de la tasa de incremento (TI) con base a los datos de severidad del tizón foliar por Cercospora durante las distintas fases reproductivas de la soya (Glycine max) en Pergamino, Buenos Aires, Argentina, 2013-2017.
| Fecha | Días | ER | I | SEV | TI |
| 17/1/2013 | 13 | R3 | 20 | 5 | 0,38 |
| 30/1/2013 | 13 | R4 | 30 | 10 | 0,38 |
| 8/2/2013 | 9 | R5 | 50 | 20 | 1,11 |
| 24/2/2013 | 16 | R6 | 80 | 30 | 0,63 |
| 12/3/2013 | 16 | R7 | 100 | 50 | 1,25 |
| 7/1/2014 | 17 | R3 | 5 | 1 | 0,06 |
| 26/1/2014 | 19 | R4 | 5 | 5 | 0,47 |
| 10/2/2014 | 15 | R5 | 15 | 10 | 0,33 |
| 27/2/2014 | 17 | R6 | 50 | 20 | 0,59 |
| 15/3/2014 | 16 | R7 | 100 | 30 | 0,63 |
| 15/1/2015 | 18 | R2 | 0 | 0 | 0 |
| 30/1/2015 | 15 | R4 | 10 | 5 | 0,33 |
| 11/2/2015 | 12 | R5 | 30 | 20 | 1,25 |
| 18/2/2015 | 7 | R6 | 50 | 30 | 1,43 |
| 30/3/2015 | 40 | R7 | 100 | 30 | 0 |
| 17/1/2016 | 11 | R3 | 7 | 2 | 0,18 |
| 29/1/2016 | 12 | R4 | 20 | 5 | 0,25 |
| 12/2/2016 | 14 | R5 | 40 | 20 | 1,07 |
| 22/2/2016 | 10 | R6 | 50 | 40 | 2 |
| 3/3/2016 | 9 | R7 | 100 | 50 | 1,11 |
| 3/1/2017 | 14 | R1 | 0 | 0 | 0 |
| 26/1/2017 | 23 | R3 | 70 | 8 | 0,35 |
| 9/2/2017 | 14 | R5 | 80 | 20 | 0,86 |
| 22/2/2017 | 13 | R6 | 100 | 40 | 1,54 |
| 3/3/2017 | 9 | R7 | 100 | 40 | 0 |
ER: estados reproductivos; I: incidencia; SEV: severidad; TI: tasa de infección desarrollo de modelos para predecir el progreso de la enfermedad. Fecha: fecha de observación de la enfermedad; Días: número de días que transcurre entre una observación y la siguiente. / ER: reproductive states; I: incidence; SEV: severity; TI: infection rate development of models to predict disease progression. Date: date of disease observation; Days: number of days between consecutive observations.
Variable dependiente
La variable dependiente fue la probabilidad de ocurrencia de niveles categorizados de TI de la SEV del TFC causado por C. kikuchii.
La categorización binaria de la TI se efectuó con relación a un valor umbral en ''niveles altos'' y ''niveles bajos''. El percentil que mejor correlacionó las variables meteorológicas y la TI fue el percentil 50 (0,47). Es decir, TI >0,47 resulta en niveles altos de SEV del TFC y TI <=0,47 resulta en niveles bajos. Las variables meteorológicas se procesaron en un lapso (período crítico) que se extendió desde la fecha correspondiente a cada fase reproductiva menos diez días. Períodos críticos menores y mayores a este valor también fueron analizados.
Variable independiente
La variable independiente o regresora se constituyó por valores diarios de temperatura máxima (Tx; °C) y mínima (Tn; °C), precipitación (Prec; mm) y humedad relativa (HR; %), provistos por la estación meteorológica convencional de la Estación Experimental Agropecuaria Pergamino, del Instituto Nacional de Tecnología Agropecuaria, Pergamino, para los años con los que se cuenta con datos de enfermedad.
A partir de estos registros meteorológicos, numerosas variables meteorológicas secundarias (térmicas, hídricas y combinadas) se calcularon en un período crítico susceptible que se extendió desde la fecha correspondiente a cada fase reproductiva menos diez días. Las mismas fueron: NDL: cuantifica el número de días con lluvias >0,5 mm; PRHR: cuantifica el número de días con lluvias >0,5 mm y HR >76 %; DHR: cuantifica el número de días con HR >76 %; DT: cuantifica el número de días con Tmax <28 °C y Tmin >15 °C; TPRE: cuantifica el número de días con Tmax <28°C, Tmin>15 °C y lluvias >0,5 mm; DHRT: cuantifica el número de días con Tmax <28 °C, Tmin >15° C y HR >76 %; MOJro: cuantifica el número de días con Tmax <28 °C, Tmin >15 °C, lluvias >2 mm y HR >75 %; MOJpr: cuantifica el número de días con Tmax <28 °C, Tmin >15 °C, lluvias >0,5 mm y HR >75 %; GDTmax: en los días donde Tmax >28 °C, GDTmax: ∑(Tmax-28 °C) (Cuadro 2).
Cuadro 2 Coeficientes de correlación de Kendall entre la tasa de incremento de tizón foliar por Cercospora en soya (Glycine max) y las variables meteorológicas. Pergamino, Buenos Aires, Argentina, 2013-2017.
| Variable | Kendall (τ) |
| NDL | -0,0504 |
| PRHR | 0,1196 |
| DHR | 0,4837 |
| DT | 0,2847 |
| TPRE | 0,2242 |
| DHRT | 0,3907 |
| MOJro | 0,4595 |
| MOJpr | 0,078 |
| GDTmax | -0,2958 |
NDL: cuantifica el número de días con lluvias >0,5 mm; PRHR: cuantifica el número de días con lluvias >0,5 mm y HR >76 %; DHR: cuantifica el número de días con HR >76 %; DT: cuantifica el número de días con Tmax <28 ºC y Tmin >15 ºC; TPRE: cuantifica el número de días con Tmax <28 ºC, Tmin>15 ºC y lluvias >0,5mm; DHRT: cuantifica el número de días con Tmax <28 ºC, Tmin >15 ºC y HR >76 %; MOJro: cuantifica el número de días con Tmax <28 ºC, Tmin >15 ºC, lluvias >2 mm y HR >75 %; MOJpr: cuantifica el número de días con Tmax <28 ºC y Tmin >15 ºC y lluvias >0,5 mm y HR >75 %; GDTmax: en los días conde Tmax >28 ºC, GDTmax: ·(Tmax-28 ºC) / NDL: quantifies the number of days with rainfall >0.5 mm; PRHR: quantifies the number of days with rainfall >0.5 mm and HR >76 %; DHR: quantifies the number of days with HR >76 %; DT: quantifies the number of days with Tmax <28 ºC and Tmin >15 ºC; TPRE: quantifies the number of days with Tmax <28 ºC, Tmin>15ºC, and rainfall >0.5 mm; DHRT: quantifies the number of days with Tmax <28 ºC, Tmin >15 ºC, and HR >76 %; MOJro: quantifies the number of days with Tmax <28 ºC, Tmin >15 ºC, rainfall >2 mm, and HR >75%; MOJpr: quantifies the number of days with Tmax <28 ºC and Tmin >15 ºC and rainfall >0.5 mm and HR >75%; GDTmax: on days with Tmax >28 ºC, GDTmax: ·(Tmax-28 ºC).
Análisis estadístico
Los modelos estadísticos se analizaron con el paquete estadístico SAS (Statistical Analysis System, versión 8.0; SAS Institute, Inc., Cary, NC, USA).
En una primera etapa, a través del procedimiento Freq de SAS, se calcularon los coeficientes de correlación no paramétricos de Kendall Tau-b (t) entre los niveles binarios de TI de la severidad del TFC categorizados y las variables meteorológicas. A partir de la maximización de estos coeficientes quedó establecida la ventana temporal donde se calcularon las variables meteorológicas.
El procedimiento Logistic del SAS se ajustó a un modelo de regresión para datos de respuesta binaria por medio del método de máxima verosimilitud (De Wolf & Isard, 2007; Moschini et al., 2006). Una función logit =ln (PrS / 1- PrS) establece la unión entre el componente estocástico y las variables regresoras meteorológicas, donde PrS es la probabilidad de una epifitia severa (S), al superar al valor umbral de TI (valor percentil que maximiza la relación entre TI y variables meteorológicas).
El modelo logístico obtenido, con X1 como predictor y β0 y β1 como parámetros fue ln (PrS/1-PrS)= β0 + β1 X1. Al resolver la expresión: 1 /(1+Exp-(ln (PrS/1-PrS)), se obtiene el valor de PrS. La probabilidad de una epifitia moderada a ligera (M) se calcula como 1 - PrS. De esta manera, los eventos son binarios PrM y PrS, donde PrM es la probabilidad de observar una epifitia moderada a ligera y la relación entre ambos: PrM=1-PrS.
Se utilizó el método de selección de variables meteorológicas regresoras Stepwise y los niveles de significancia a priori, para entrar y permanecer en el modelo (NSE y NSP, respectivamente).
Derivado del análisis de regresión logística, se calcularon para cada modelo ajustado la sensibilidad (porcentaje de observaciones epifíticas > al valor umbral mediana de SEV predichas como S), especificidad (% de observaciones epifíticas <= al umbral clasificado como M), falsos S y falsos M. Sensibilidad y especificidad de los modelos se utilizaron para calcular la precisión de predicción (Hughes et al., 1997).
La precisión de predicción es el porcentaje de casos clasificados. Si en cada uno de los casos analizados se compara la TI observada versus la predicha con la máxima probabilidad de ocurrencia por las ecuaciones logísticas desarrolladas, es posible calcular el porcentaje de casos correctamente clasificados.
Resultados
Las variables meteorológicas con mayor coeficiente de Kendall se presentan en el Cuadro 2. La variable DHR presentó el mayor coeficiente de correlación (t =0,4837) y correspondió a una variable simple compuesta por la humedad relativa. MOJro (t =0,4595) y DHRT (t =0,3907) son variables compuestas que además de humedad relativa tienen temperatura y lluvia como componente. La inclusión de cada uno de estos dos últimos elementos meteorológicos no contribuyó para superar a la variable simple (DHR).
Las variables relacionadas al elemento lluvia (NDL, PRHR y MOJpr) tuvieron muy baja correlación. Entre las variables relacionadas con la temperatura, GDTmax resultó la de mayor correlación (-0,2958) y con pendiente negativa. Esto indica que a mayor número de días con temperaturas >28 °C, es menor la TI del TFC. Variables térmicas que representan condiciones óptimas para el desarrollo de la enfermedad (DT) presentaron baja correlación, lo que indicaría que para este conjunto de datos (cinco años), DT no tuvo un rol importante en el desarrollo del TFC.
El procedimiento Stepwise del proc logistic, con un nivel de significancia de 0,05 %, seleccionó el modelo constituido por DHR y GDTmax como el más apropiado (Cuadro 3). El umbral de riesgo (Cuadro 3; Figura 1), corresponde al valor de probabilidad (p=0,47) para clasificar la ocurrencia de niveles categorizados (bajo y alto) de TFC. El mismo se determinó con la sensibilidad y la especificidad para el rango completo de valores de probabilidad. Se eligió el valor que maximizó la sensibilidad y especificidad. La probabilidad de riesgo severo del TFC obtenida entre los años 2018-2019 (línea negra) y umbral de riesgo (línea roja) se observan en la Figura 1. En dichos años, los niveles de SEV del TFC superaron el umbral de riesgo del 16 al 25 de diciembre de 2018 y del 15 al 25 de enero de 2019, lo cual indicaría la necesidad de la aplicación de fungicidas foliares para el control de la enfermedad.
Cuadro 3 Modelo de regresión logística para estimar la probabilidad de ocurrencia de niveles categorizados como bajos o altos de tizón foliar por Cercospora en soja (Glycine max). Pergamino, Buenos Aires, Argentina, 2013-2017.
| Modelo | ||||
| Logist=-0,8524 + 0,4152 DHR -0,0420 GDTmax | ||||
| Concordancia | Precisión | Sensibilidad | Especificidad | p |
| 82,1 % | 84 % | 75 % | 92 % | 0,47 |
Logist=ln (PrS/1-PrS), siendo PrS la probabilidad de ocurrencia de una epifitias severa (S) y ln es el logaritmo natural. Al resolver la expresión 1 / (1+Exp-Logit) se obtiene el valor de PrS. Evento binario: PrM=1-PrS, siendo PrM probabilidad de observar una epifitia moderada a ligera, DHRT: cuantifica el número de días con Tmax <28 ºC, Tmin >15º C y HR >76 %; GDTmax: en los días donde Tmax >28 ºC, GDTmax: ·(Tmax-28 ºC). / Logist=ln (PrS/1-PrS), where PrS is the probability of occurrence of a severe epidemic (S), and ln is the natural logarithm. By solving the expression 1 / (1+Exp-Logit) yields the value of PrS. Binary event: PrM=1-PrS, where PrM is the probability of observing a moderate to mild epidemic. DHRT: quantifies the number of days with Tmax <28 ºC, Tmin >15 ºC, and HR >76 %; GDTmax: on days with Tmax >28 ºC, GDTmax: ·(Tmax-28 ºC).
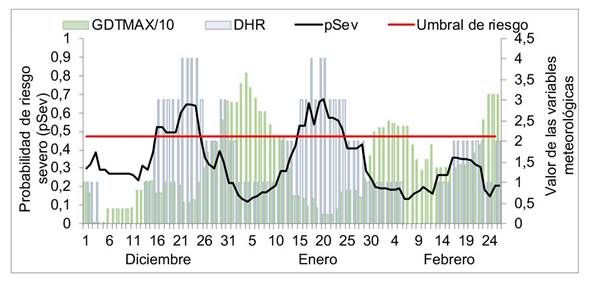
Figura 1 Evolución de la probabilidad de ocurrencia diaria de TI del tizón foliar por Cercospora (pSev) en soya (Glycine max) y de los valores de las dos variables predictoras meteorológicas DHR (número de días con HR>76%); GDTmax (cuando Tmax>28 acumula los residuales diarios) para los años 2018 y 2019 en Pergamino, Buenos Aires, Argentina. 2013-2017.
Discusión
El nuevo modelo para el tizón foliar por Cercospora (TFC) en soja englobó dos variables climáticas importantes para el desarrollo de la enfermedad (días con humedad relativa >76 % (DHR) y días donde temperaturas máximas >28 °C (GDTmax)). Estudios realizados sobre las enfermedades de final de ciclo en soja, solo utilizaron como variable de respuesta a las precipitaciones (Carmona et al., 2010). Sin embargo, en esta investigación no solo son importantes los días con humedad relativa (HR) superior al 76 %, sino que las temperaturas también influyeron en la evolución del TFC en el norte de la provincia de Buenos Aires. Estos resultados son congruentes con los publicados en mijo perla (Pennisetum glaucum), con un aumento significativo de la severidad de las enfermedades con valores elevados de humedad y temperaturas durante el ciclo del cultivo (Yadav et al., 2016).
Otros antecedentes en modelos predictivos que refuerzan los resultados obtenidos en la presente investigación, donde no solo las precipitaciones fueron importantes en la evolución de una enfermedad, fueron los obtenidos en Luxemburgo para roya amarilla causada por Puccinia striiformis del trigo (Triticum aestivum), en dicha investigación se obtuvo que en invierno se requieren elevadas humedades relativas (>92 %), temperaturas entre los 4 °C y los 16 °C, y por lo menos cuatro horas por día para que la enfermedad se desarrolle y pueda causar una epifitia (El Jarroudi et al., 2017). Además, en trigo se ha observado una mayor relación con la humedad relativa que con la temperatura, para la evolución de la severidad del quemado del trigo o Pryricularia o Brusone del trigo causado por Magnaporthe oryzae pathotype Triticum en Asia (Montes et al., 2022).
El modelo propuesto en esta investigación fue validado con los datos de severidad del TFC obtenidos en campo durante los años 2018, 2019 y 2020 en el norte de la provincia de Buenos Aires. Esta validación fue congruente entre la curva predicha con el modelo sobre la evolución del TFC y con las variables patométricas relevadas a campo.
En esta investigación los bajos coeficientes de correlación de Kendall (Cuadro 2) de todas las variables en general, indican que se necesita continuar con la evaluación del TFC sobre el cultivo de soja en los próximos años y robustecer así el modelo propuesto.
Este es el primer modelo predictivo del TFC que asocia a la humedad relativa y las temperaturas, con la intensidad de la enfermedad.
Conclusión
Se pudo desarrollar un modelo de predicción de la severidad del TFC que incluyó dos variables meteorológicas, una relacionada con los días de humedad relativa y otra térmica relacionada con el límite de temperatura máxima para el óptimo desarrollo de la enfermedad. Para validar y robustecer el modelo propuesto, es necesario contar con más datos de severidad a través de los años.