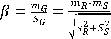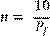Introducción

El proyecto eBridge nace a partir de un problema nacional (Costa Rica) en cuanto a renovación y mantenimiento de sus infraestructuras, que muchas veces se clasifican como estructuralmente deficientes, puesto que ya alcanzaron el límite de su vida útil de servicio y no son sometidas a ningún proceso de rehabilitación. Al respecto, los puentes de uso vial están entre los más afectados.

Es por esta razón que instituciones del Estado de Costa Rica entre ellas el Ministerio de Obras Públicas y Transportes y el Consejo Nacional vieron la oportunidad de colaborar en el mejoramiento de la infraestructura vial existente, mediante la propuesta de metodologías que permitan la predicción remota de fallas en los puentes. En este sentido, se consideró necesario crear un modelo de confiabilidad integrando variables aleatorias experimentales obtenidas mediante diferentes métodos de simulación.

Los actuales procedimientos analíticos avanzados permiten un análisis numérico exacto pero determinista de la relación tensión/esfuerzo de los componentes de un puente. Existen procedimientos matemáticos para el cálculo de la confiabilidad de los diversos sistemas idealizados: paralelo, serie y combinaciones, así como también hay novedades en cuanto a los materiales, la tecnología y las pruebas de campo que se pueden utilizar para mejorar el diseño del puente y su evaluación [¹].

Es de especial interés mencionar que en el pasado se realizaron estudios sobre la detección de daños en las estructuras, la mayoría basados en parámetros dinámicos; además de los avances tecnológicos detectados en la creación de sensores y sistemas de adquisición de datos. En algunas evaluaciones estructurales en obras civiles, se ha comprobado que es posible utilizar el cambio de los parámetros dinámicos para determinar el daño en una estructura [²]. Pero no es sino hasta años recientes que en Costa Rica se está implementando la predicción de manera remota de estos daños o fallas, lo que la hace innovadora en su área; además de que mezcla varias disciplinas ingenieriles para la obtención y análisis confiable de la información.

Lo que se espera al final de este proyecto es un sistema experto que permita determinar la vida útil de los puentes a través de un modelo de confiabilidad estructural, para poder determinar cuándo es necesario su mantenimiento, rehabilitación o reemplazo antes de que colapsen o queden inhabilitados.

Marco teórico

Los conceptos teóricos que fundamentan este trabajo se muestran a continuación. Es importante mencionar que un modelo de confiabilidad es una ecuación matemática que pretende determinar la probabilidad de ocurrencia de una falla [³]

El modelo de confiabilidad estará en función del estado límite, que se puede definir como ^[1]

G = R - S = 0 Margen de seguridad ( Ecuación 1)

donde:

R: Resistencia (capacidad momento)

S: Efecto de carga (momento aplicado)

De esta manera, si G > 0, se afirma que la estructura es segura, de lo contrario se considera que la estructura estaría en riesgo de falla. Con respecto a la probabilidad de falla, se tiene:

P_f = Prob (R - S < 0) = Prob (G < 0) ( Ecuación 2)

Los conceptos estadísticos de confiabilidad se desarrollan por medio de la determinación del Índice de Confiabilidad (β), que se define como la inversa de la función estándar acumulada de la probabilidad de falla (P_f) [⁴]):

β = F^-1 (P_f) ( Ecuación 3)

La distribución de la función límite (G) está determinada por la zona de falla donde la media de la función G (m_G) es proporcional a la desviación estándar (S_G). La proporción de estos dos parámetros es el índice de confiabilidad (β) y, asumiendo una distribución normal, esta puede evaluarse como:

m_G = β * S_G ( Ecuación 4)

( Ecuación 5)

donde:

m_R, m_S: medias de la distribución de la resistencia y las cargas

S_R, S_s: desviaciones estándar de la distribución de la resistencia y las cargas.

Los índices de confiablidad de tres códigos internacionales para el análisis de confiabilidad estructural en puentes, según [⁵]son los siguientes:

En cuanto a las aplicaciones, ventajas y desventajas del uso de la simulación Monte Carlo como una herramienta útil para modelar fenómenos con cierto grado de incertidumbre, las más importantes son confiabilidad, disponibilidad, logística, pronósticos, análisis del riesgo y análisis de interferencias carga-resistencia, lo que es altamente relacionable con el objetivo de la investigación. Se trata de un método iterativo de simulación para evaluar un modelo determinístico utilizando variables y números aleatorios. Se fundamenta en conocer a priori las distribuciones de probabilidad de las variables bajo estudio. Los datos generados por una simulación pueden ser representados y analizados mediante técnicas estadísticas tradicionales ^[2]

Ebeling [⁶]describe y aplica los pasos a seguir para la adecuada selección de una distribución de probabilidad teórica para una variable aleatoria continua o discreta, mediante pruebas de bondad de ajuste. Las pruebas recomendadas son Anderson Darling, Kolmogorov-Smirnov y Ryan-Joiner. Los valores típicos del nivel de significancia utilizado son α = 0.05 y 0.10.

Por último, cabe mencionar que una prueba de carga es la medición de la respuesta de una estructura de un puente sujeto a cargas conocidas y controladas sin que se causen cambios en la respuesta elástica de esta [⁷].

Desarrollo

En esta investigación se efectuaron tres pruebas de carga, con los siguientes objetivos principales [⁸]: Determinar las deformaciones, desplazamientos en juntas, desplazamientos verticales en vigas y aceleraciones asociadas a las cargas dadas.

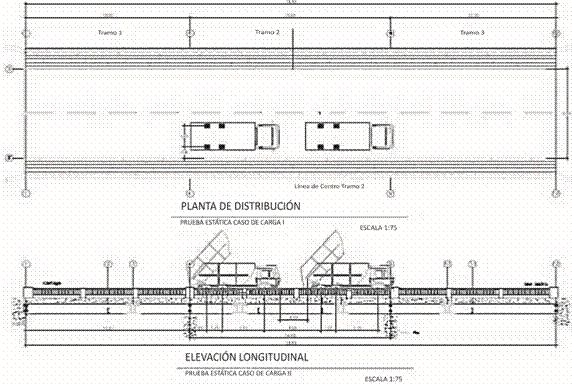
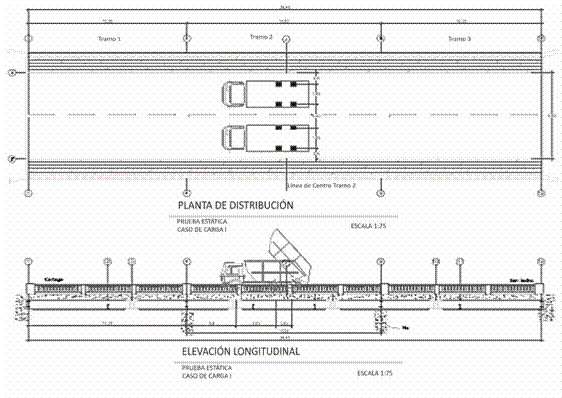
El tipo de prueba realizada, así como su caso de carga, se detalla en el Cuadro 1.

Cuadro 1 Tipos de pruebas realizadas en Purires 

En las Figuras 1 y 2 se ejemplifican el Caso I y el Caso II, respectivamente:

Figura 1: Prueba estática del Caso de carga I 

Puente seleccionado: Río Purires, El Guarco, Cartago

El puente llamado “Purires” se ubica en la ruta nacional número 2. Es un puente de vigas continuas de acero W27X94, de 39,45 m de longitud total y una distancia promedio entre apoyos menor a 15 m. Cuenta con cuatro puntos de apoyo. Posee una losa de concreto de 15 cm de espesor con refuerzo de acero #6 cada 15 cm de forma transversal y cada 25 cm longitudinalmente y una sobre capa de asfalto que varía entre 14 y 7 cm de espesor.

Figura 2: Prueba estática del Caso de carga II 

El puente cuenta con dos carriles y doble vía y el promedio diario de vehículos que transitan por él es de 11,318 (conteo vehicular proporcionado por el Ministerio de Obras Públicas y Transportes, MOPT), el ancho de la superficie de ruedo es de 6,6 m y dispone de aceras de 1,5 m. La distancia libre desde el río tiene un promedio de 5 m. Se estima que este puente se construyó en los años 50, aunque se desconoce la fecha exacta [⁹].

• Propiedades del material

• Acero A33. W 27x94

• Módulo de elasticidad = 2,038,901,78 kg/cm²

• Esfuerzo de fluencia kg/cm²: Promedio: 2574.78, desviación estándar: 295.72. ^[3].

• Pruebas estáticas

• Tomado de protocolo presentado por Carvajal [¹⁰].

• Prueba estática: Caso I.

• Prueba estática: Caso II

• Prueba estática: Caso IIa

• Análisis estructural realizado con el programa SAP2000

• Pruebas de bondad de ajuste para los valores de deformaciones (strains)

• Las pruebas de hipótesis a probar es la siguiente:

H_o: datos siguen una distribución normal

H₁: datos no siguen una distribución normal

Para la prueba de hipótesis se utilizará un nivel se significancia α = 0.05.

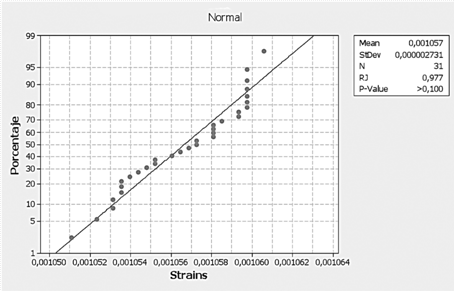
Caso I: Valor P (0.10) > α. No hay suficiente evidencia estadística para concluir H₁. Los datos siguen una distribución normal (Figura 3).

Figura 3: Gráfico de probabilidad Caso I 

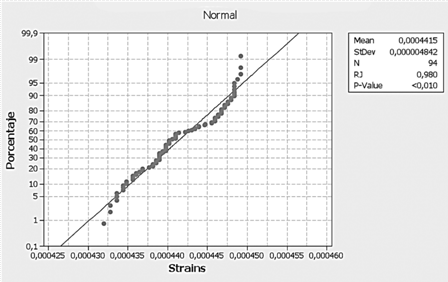
Caso II: Valor P (0.010) < α. Hay suficiente evidencia estadística para concluir H₁. Los datos no siguen una distribución normal (Figura 4).

Figura 4: Gráfico de probabilidad Caso II 

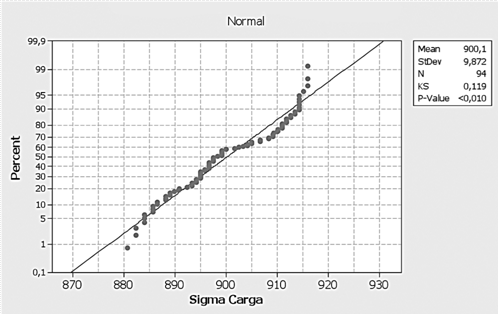
Caso III: Valor P (0.010) < α. Hay suficiente evidencia estadística para concluir H₁. Los datos no siguen una distribución normal (Figura 5).

Figura 5: Gráfico de probabilidad Caso IIa. 

• Los resultados del escenario de simulación I se muestran en el Cuadro 2.

Cuadro 2 Resultados de escenario de simulación I 

• Para realizar el escenario de simulación II es necesario calcular el número de réplicas, con base en la fórmula propuesta por Estes ^[3]:

donde Pf es tomado del escenario de simulación I.

• Los resultados del escenario de simulación II se muestran en el Cuadro 3.

Figura 6: Distribución de esfuerzo versus resistencia. Caso I 

Figura 7: Distribución de carga versus resistencia. Caso II 

Figura 8: Distribución de carga versus resistencia. Caso IIa 

Cuadro 3 Resultados de escenario de simulación 

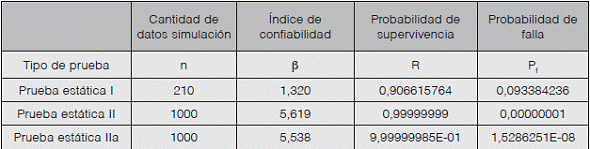
(*) Cuando n es muy grande, se utilizan 1000 réplicas.

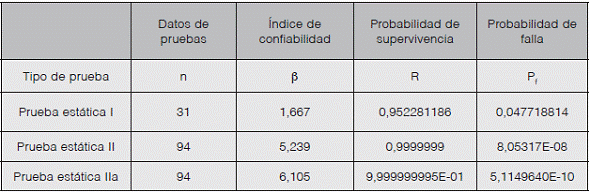
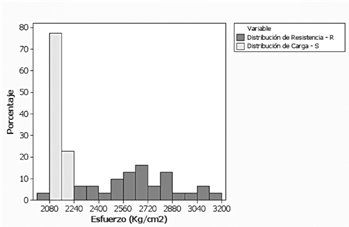
• En relación con la prueba estática de carga I (cuadro 2) con un índice de confiabilidad β = 1.6677, no se cumple con los requerimientos de ningún código internacional para el análisis estructural de puentes. La figura 6 representa el comportamiento de los valores de carga y resistencia. Se recomienda revisar el protocolo de carga utilizado en esta prueba y el análisis estructural realizado para analizar con mayor detalle las causas y efectos de un índice de confiabilidad bajo.

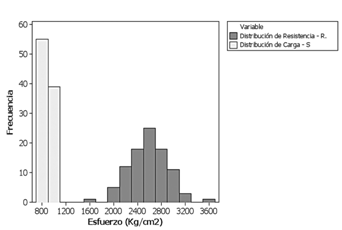
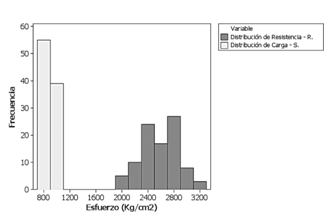
• Los índices de confiabilidad para las pruebas estáticas de carga II y IIa (cuadro 2) cumplen satisfactoriamente los requerimientos de los códigos Español y AASHTO; sin embargo, no satisface los requerimientos del código Europeo. Las figuras 7 y 8 representan el comportamiento de los valores de carga y resistencia en ambos escenarios.

• Sobre los resultados del escenario de simulación II (cuadro 3), se mantienen las mismas conclusiones anteriores, donde la prueba estática I no satisface los requerimientos de los códigos internacionales, mientras las pruebas estáticas II y IIa sí cumplen satisfactoriamente los requerimientos internacionales.

• Es importante analizar con más detalle el comportamiento no normal de algunos datos de deformaciones (strains) en dos pruebas de carga estática, ya que el análisis posterior para el cálculo del índice de confiabilidad asume una distribución normal.

• Se sabe actualmente que el puente sobre el río Purires presentó una falla de magnitudes importantes en cuanto a deformaciones (Caso I). Esto indica que si se hubieran realizado las pruebas a tiempo, se hubiera podido intervenir el puente y atender a tiempo la falla, todo esto si se toma en consideración que el valor de probabilidad de falla es de P_f= 0.047, lo cual es muy alto ya que es de casi un 5%, si se compara este valor con un α = 0.05 que equivale a un 95% de nivel de confianza.

Conclusiones y recomendaciones

Se hacen las siguientes recomendaciones: