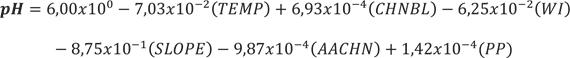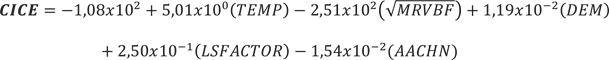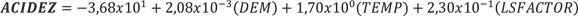INTRODUCCIÓN
Los atributos del suelo a partir del cono- cimiento de la variabilidad espacial es deter- minante para una adecuada gestión del recurso suelo (Heuvelink y Webster 2001, McBratney et al. 2003). El manejo de la fertilidad de los suelos, basado en un conocimiento preciso y actuali- zado, implica beneficios en la productividad y sostenibilidad de los cultivos (Henríquez et al. 2005, Villatoro et al. 2008). Es así como el mapeo digital de suelos (MDS) propone la determina- ción y cuantificación de la distribución espacial de los atributos y clases de suelos, a través del desarrollo de sistemas empíricos de inferencia entre las observaciones del suelo y un conjunto de variables representativas del paisaje referen- ciadas espacialmente (Lagacherie 2008, Grimm y Behrens 2010, Malone et al. 2017).
Entre las ventajas que se acreditan al MDS, se pueden citar la generación de produc- tos en menor tiempo y costos, la construcción de inferencias estadísticas entre información de muestreos y características ambientales, la posi- bilidad de construir representaciones gráficas bajo un modelo de variación espacial continua, y la posibilidad de aplicar el MDS en lugares donde el acceso y la información de suelos son limitados (Cambule et al. 2013, Malone et al. 2017). Asi- mismo, el MDS permite la estimación de la incer- tidumbre, asociada a las predicciones realizadas; esta incertidumbre puede ser causada por incon- sistencias en el muestreo de suelos, diferencias en las metodologías analíticas empleadas, errores de laboratorio y de posicionamiento espacial, errores propios de las covariables ambientales y la falla propia de la técnica de modelización empleada (Heuvelink 2017), en términos generales evaluar la incertidumbre permite conocer la calidad del producto cartográfico generado.
La cartografía de propiedades de suelos se ha construido mediante distintas técnicas de análisis espacial, cada una con fortalezas y limi- taciones metodológicas, se pueden citar algunos ejemplos donde se utilizaron los métodos: geo- estadísticos (Henríquez et al. 2005, Henríquez et al. 2013, Pravat et al. 2016, Garbanzo et al. 2017), determinísticos (Villatoro et al. 2008, Fortis-Her- nández et al. 2010), árboles de regresión (Scull et al. 2005, Taghizadeh-Mehrjardi et al. 2014) y machine learning (Brungard et al. 2015, Heung et al. 2016). No existe una técnica de modeliza- ción que pueda considerarse superior a otra, cada una puede o no funcionar mejor en contextos diferentes. De acuerdo a ejercicios realizados en contextos similares, los modelos lineales han pre- sentado un mejor desempeño en la modelización (modelos con menor incertidumbre) frente a téc- nicas de modelización del campo del aprendizaje automatizado, tales como Random Forest, que se plantean muy favorables por ser no paramétricas; otra ventaja de los modelos lineales es que su interpretación resulta práctica (Richardson et al. 2017, Búcaro 2017).
McBratney et al. (2003) proponen un modelo conceptual para el abordaje del MDS, este se denomina scorpan-SSPFe; el primer tér- mino del nombre hace referencia a una adapta- ción de la ecuación de los factores formadores del suelo propuesta por Jenny (1941), mientras que el sufijo hace referencia al término: funcio- nes de predicción espacial de suelos con errores autocorrelacionados. Ambos términos explican conceptualmente las bases del modelo.
Con la finalidad de evaluar los alcances MDS, a partir de modelos lineales en condicio- nes de suelos tropicales, se desarrolló un ejer- cicio en la región Occidental del Valle Central de Costa Rica con el objetivo de generar mapas de la variabilidad espacial de los atributos: pH, acidez y CICE; en una región de aptitud agro- pecuaria de Costa Rica. Estas variables fueron consideradas al aprovechar los recursos fácil- mente disponibles y aprovechando su relevancia en la gestión sostenible de la productividad del suelo. Como insumos se emplearon las bases de información geográfica de 3 cooperativas agrí- colas ubicadas en la región (CoopeAtenas R.L., CoopeVictoria R.L. y CoopAgrimar R.L.), el modelo de elevación digital e imágenes satelita- les de la región de estudio.
MATERIALES Y MÉTODOS
El área de estudio abarcó parte de la Región Occidental del Valle Central, que incluye sectores de los cantones Alajuela, Atenas, San Ramón, Zarcero y Grecia, todos de la provincia Alajuela, Costa Rica. El área de estudio contó con una extensión aproximada de 1884 km2, con una geodinámica externa que está dominada por relieves multiconvexos, principalmente en la parte Sur de la zona de estudio; las llanuras y las mesetas entalladas por profundos cañones de ríos se localizan en el sector central, mientras los edificios volcánicos y los piedemontes del Terciario y Cuaternario dominan en la parte Norte (Bergoeing 1998). La variabilidad del relieve y de materiales parentales, aunado a los contrastes de temperatura y precipitación, gene- ran la ocurrencia de asociaciones edáficas domi- nadas por Ustands, Humults, Ustepts y Orthents (Mata et al. 2013). Los suelos del área de estudio se destinan principalmente a actividades agro- pecuarias, donde predominan los cultivos de café, caña de azúcar, pasturas y hortalizas, entre otros (Figura 1).
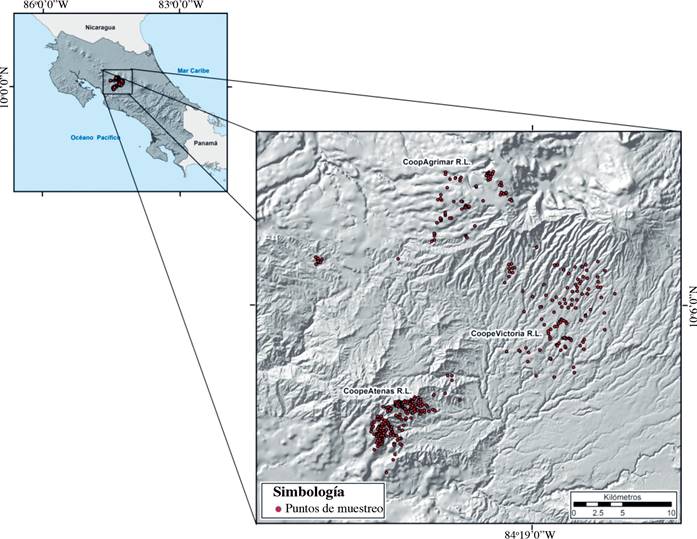
Fig. 1. Ubicación general del área de estudio ubicada en la región Occidental del Valle Central de Costa Rica.
Se utilizaron los registros georreferencia- dos de 384 análisis químicos de suelos con fines de fertilidad realizados entre 2012 y 2015 en las cooperativas CoopAgrimar R.L., CoopeAtenas R.L. y CoopeVictoria R.L., todas ellas dentro del área de estudio propuesta. El muestreo se llevó a cabo en el marco de un proyecto colaborativo y cofinanciado entre la Universidad de Costa Rica (UCR) y el Instituto de Fomento Coope- rativo (INFOCOOP). Se recolectaron muestras compuestas por cada lote previamente georre- ferenciado. Cada una estuvo constituida de 15 submuestras distribuidas aleatoriamente dentro del lote y colectadas de los primeros 20 cm superficiales. La georreferenciación de los aná- lisis de fertilidad se realizó a través de la asig- nación de dicha información al centroide del polígono que delimitaba cada lote muestreado.
Además, de la recopilación de estas mues- tras de suelos, se construyeron 24 capas de variables asociadas a los factores de formación del suelo que serían utilizadas como covariables (Cuadro 1). Para la construcción de estas capas se consideró el modelo conceptual scorpan-SSPFe. Con una adaptación de la ecuación propuesta para explicar cuantitativamente la relación entre los factores formadores del suelo y su génesis (Jenny 1941).
Cuadro 1 Fuentes y variables predictoras generadas para desarrollar los modelos de predicción.
| Covariables de imagen LANDSAT 8 | 12 Sombreado Analítico (ANAHILL) |
| 1 Banda 1 | 13 Pendiente (SLOPE) |
| 2 Banda 2 | 14 Aspecto (ASPECT) |
| 3 Banda 3 | 15 Curvatura del Plano (PLANC) |
| 4 Banda 4 | 16 Curvatura del Perfil (PROFILEC) |
| 5 Banda 5 | 17 Índice de Convergencia (CONINDEX) |
| 6 Banda 6 | 18 Área de Acumulación (CATAREA) |
| 7 Banda 7 | 19 Índice de Humedad (WI) |
| Covariables de Registros Climáticos | 20 Factor de Largo de Pendiente (LSFACTOR) |
| 9 Temperatura (TEMP) | 21 Nivel Base de la Red de Drenaje (CHNBL) |
| 10 Precipitación (PP) | 22 Altura sobre la Red de Drenaje (AACHN) |
| Covariables del DEM | 23 Índice Multirresolución Depresional de Valles (MRVBF) |
| 11 Altitud (DEM) | 24 Índice Multirresolución de Llanura de Crestas (MRRTF) |
El modelo queda representado por la siguiente ecuación:
Sc = f( s,c,o,r,p,a,n)+e,
Sc = representa el atributo o clase del suelo a modelizar o predecir, como una función de
S = suelo (observaciones previas de clases o atri- butos del suelo);
c = clima (precipitación, temperatura, evapo- transpiración, etc.);
o = organismos (actividad biótica o antrópica);
r = relieve (atributos del paisaje geomorfológico); p = material parental (litología asociada a un punto determinado);
a = edad (tiempo transcurrido para la génesis del suelo) y
n = espacio o posición espacial.
Finalmente, se hace referencia a la incerti- dumbre asociada al modelo, es decir, a las predic- ciones de los atributos o clases de suelos.
Aunque en este caso no se pretende su uso para explicar la pedogénesis, sino para describir de forma empírica y cuantitativa las relaciones entre el suelo y otras variables espacialmente referenciadas que describen su ambiente o paisaje.
Fueron empleados 4 insumos básicos para la construcción de las capas predictoras: el mode- lo de elevación digital (DEM) con una resolución espacial de 30 m, una imagen LANDSAT 8 OLI del área de estudio correspondiente a la época seca y 2 capas climáticas (precipitación y tem- peratura media anual) de la región de estudio (Cuadro 1). A partir del DEM se construyeron 14 capas de atributos morfométricos primarios y secundarios para utilizarlos como predictores representativos del relieve; de la imagen LAND- SAT 8 OLI se emplearon las bandas 1 a 7 y un NDVI como predictores representativos de los organismos. Las capas de precipitación y tempe- ratura también fueron empleadas como predicto- res representativos del clima.
Para cada punto asociado a un análisis de fertilidad se extrajeron los valores correspon- dientes de las 24 capas predictoras o covariables, los cuales conformaron la base de datos que se empleó en la modelización de los atributos pro- puestos. Se seleccionaron aleatoriamente y sepa- raron del conjunto de datos 84 observaciones que se emplearon posteriormente en la validación de los resultados (Henríquez et al. 2013). Se realizó una modelización de los atributos (pH, Acidez y CICE) como función de las variables predictoras generadas al emplear modelos lineales, se utili- zaron los algoritmos de selección de variables paso a paso desde su introducción y eliminación progresiva con la finalidad de obtener mode- los más parsimoniosos. Se seleccionó el mejor modelo obtenido para cada atributo con base en el Criterio de Información de Akaike (CIA), el cual indica la calidad relativa del modelo a par- tir de las variables utilizadas; por tanto, el CIA sólo tiene sentido cuando se comparan modelos creados a partir del mismo conjunto de datos.
También se realizó el proceso de validación para corroborar la consistencia de la incertidumbre asociada a cada modelo (Villatoro et al. 2008, Garbanzo-León et al. 2017). Se evaluó la autoco- rrelación espacial de los residuos de cada modelo para la realización del krigaje de los mismos. La capa de los residuos interpolados se sumó a la capa generada para cada modelo lineal, res- pectivamente, lo cual generó un nuevo modelo. Se extrajeron los valores predichos del nuevo modelo para los puntos de validación y se realizó nuevamente el proceso de validación según la propuesta de McBratney et al. (2003). Se selec- cionó el mejor modelo obtenido y se construyó un mapa para cada atributo propuesto, utilizando algebra de mapas.
RESULTADOS Y DISCUSIÓN
Al evaluar el CIA para los modelos de pH, el modelo lineal que presentó mejor desempeño predictivo para el pH de suelo fue:
En donde pH es el valor predicho de pH del suelo en agua (relación suelo agua 1:2.5), TEMP es la temperatura media anual (°C), CHNBL es la altura basal del nivel de drenaje (m), WI es el índice de humedad (adimensional), SLOPE es el valor de pendiente (%), AACHN es la altura sobre el nivel basal de drenaje (m) y PP es la precipitación media anual (mm). La combinación de dichas covariables presentó como resultado la variación espacial del pH que se presenta en la Figura 2A. El modelo seleccionado evidenció un aumento del pH cuando aumentaba CHNBL y PP, caso contrario sucedió con las restantes 4 covariables seleccionadas.
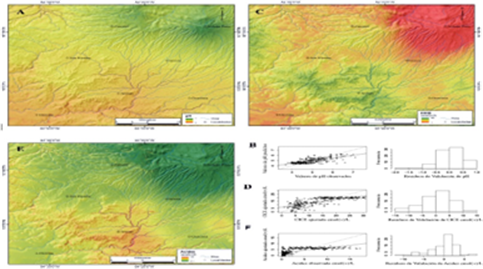
Fig. 2. Variables predictoras generadas para la realización de los ejercicios de MDS. (A) Mapa de pH generado a partir del modelo descrito. (B) Gráfico de dispersión de valores observados contra predi- chos para el modelo de pH e histograma de residuos de validación. (C) Mapa de CICE generado a partir del modelo descrito. (D) Gráfico de dispersión de valores observados contra predichos para el modelo de CICE e histograma de residuos de validación. (E) Mapa de Acidez generado a partir de modelo descrito. (F) Gráfico de dispersión de valores observados contra predichos para el modelo de acidez e histograma de residuos de validación
Este modelo alcanzó a explicar el 51% de la variación en el pH (según R2), al emplear 6 variables predictoras, y presentó un error están- dar residual de 0,45. Los resultados de validación evidenciaron una desviación estándar de los residuos de 0,49, promedio absoluto del error de 0,37, promedio de los errores de 0,24. Estos datos demuestran la consistencia de la incertidumbre asociada al modelo. La consistencia entre la incertidumbre propia del modelo y la incertidum- bre evaluada, a través de la validación, radica en la similitud entre el error estándar residual del modelo y la desviación estándar de los residuos de validación. La diferencia de 0,04 unidades de pH entre ambos datos puede explicarse por la diferencia en el tamaño de la muestra de los datos empleados para entrenar el modelo (n=300) y los empleados en la validación (n=84).
El desempeño de predicción del modelo para el pH se consideró aceptable, ya que se encontró consistencia del modelo en relación con el cumplimiento de los supuestos de la regresión lineal múltiple. Asimismo, el error estándar residual se interpreta al estimar que, aproximadamente con un 70% de confiabili- dad, el valor real de pH se encontrará entre el intervalo que va del valor predicho ±0,45 (Figura 2B). De acuerdo con el análisis de varianza y a los análisis de sensibilidad reali- zados, el factor con mayor poder predictor es la temperatura, seguida por la pendiente, el nivel base de red de drenaje, la altura sobre el nivel de drenaje, el índice de humedad y la precipi- tación, respectivamente.
Para el caso de la CICE, el modelo lineal que presentó mejor desempeño predictivo fue:
En donde CICE es el valor predicho de CICE (cmol(+).l-1), TEMP es la temperatura media anual (°C), MRVBF es el índice multirresolución depresional de valles (adimensional), DEM es el valor de altitud en metros sobre el nivel del mar (m), LSFACTOR es el valor del índice de largo de pendiente (adimensional) y AACHN es la altura sobre el nivel basal de drenaje (m); para este caso la variación espacial de la CICE del suelo en la región de interés se presenta en la Figura 2C.
Este modelo alcanzó a explicar el 52% de la variación en la CICE (según R2) al emplear 5 variables predictoras y presentó un error estándar residual de 5,94 cmol(+).l-1. Los resultados de validación evidenciaron una desviación estándar de los residuos de 5,87 cmol(+).l-1, un prome- dio absoluto del error de 4,53 cmol(+).l-1 y un promedio de los errores cuadrados de 34,37 (cmol(+).l-1)2. Estos datos demuestran la consis- tencia de la incertidumbre asociada al modelo.
Con base en los resultados, se consideró que el desempeño de predicción del modelo para la CICE es medianamente aceptable. Al consider la consistencia del modelo en relación con el cumplimiento de los supuestos de la regresión lineal múltiple, el error estándar residual se interpreta al estimar que, aproximadamente, con un 70% de confiabilidad el valor de real de CICE, se encontrará entre el intervalo que va del valor predicho ±5,94 cmol(+).l-1 (Figura 2D). De acuerdo con el análisis de varianza y los análisis de sensibilidad realizados, el factor con mayor poder predictor es la temperatura, seguida por la altitud, la raíz cuadrada del índice multirre- solución depresional de valles, la altura sobre el nivel de drenaje y el factor de largo de pendiente, respectivamente. Una de las limitaciones noto- rias en el modelo es que no se alcanza a explicar aceptablemente la variación de los valores arriba de 20 cmol(+).l-1, ya que tiene limitaciones para capturar la variación espacial local de la CICE, por lo cual es recomendable evaluar otras fuentes de información para generar nuevas variables predictoras; otro factor puede estar relacionado con la cantidad de observaciones utilizadas para la validación del modelo.
Por otra parte, el modelo que presentó mejor desempeño para la acidez fue:
En donde ACIDEZ es el valor predicho de la acidez intercambiable (cmol(+).l-1), DEM es el valor de altitud en metros sobre el nivel del mar (m), TEMP es la temperatura media anual (°C) y LSFACTOR es el valor del índice de largo de pendiente (adimensional); lo cual dio como resul- tado la Figura 2E.
Este modelo alcanzó a explicar un 42% de la variación en la acidez (según R2), al emplear 3 variables predictoras, y presentó un error estándar residual de 3,18 cmol(+).l-1. Los resultados de la validación evidenciaron una desviación estándar de los residuos de 3,30 cmol(+).l-1, un promedio absoluto del error de 2,44 cmol(+).l-1 y un promedio de los errores cuadrados de 10,80 (cmol(+).l-1)2. Estos datos demuestran la consistencia de la incertidumbre asociada al modelo.
Al igual que los prototipos anteriores, el desempeño de predicción del modelo para la acidez se consideró medianamente aceptable. Al considerar la consistencia del modelo en relación con el cumplimiento de los supuestos de la regresión lineal múltiple, el error estándar residual se interpreta al estimar que con un 70% de confiabilidad el valor de real de acidez se encontrará entre el intervalo que va del valor predicho ±3,18 cmol(+).l-1 (Figura 2F). De acuer- do con el análisis de varianza y a los análisis de sensibilidad realizados, el factor con mayor poder predictor es la temperatura, seguida por la altitud y el factor de largo de pendiente, respec- tivamente. Este modelo logra explicar la varia- bilidad espacial de la acidez de forma global, al sacrificar las tendencias locales; por tanto, una de las limitaciones notorias en el modelo es que no se alcanza a explicar aceptablemente la variación de los valores arriba de 9 cmol(+).l-1, como en el caso anterior es recomendable eva- luar otras fuentes de información para generar nuevas variables predictoras.
CONCLUSIÓN
Los Modelos Digitales de Suelos (MDS) demostraron ser una herramienta potencialmente aplicable para la obtención de información útil en la estimación de la fertilidad de suelos a nivel regional en un escenario multifactorial lo cual aporta conocimientos más precisos y actuales res- pecto a la variabilidad espacial de los atributos y clases del suelo; asimismo, representa beneficios en términos de productividad y sostenibilidad en los cultivos. Aunque los modelos generados pre- sentaron una fracción de incertidumbre asociada, se evidencia que representan una herramienta aplicable con menores costos y menos tiempo de ejecución, que genera representaciones de la variabilidad espacial continua, utilizables para la toma de decisiones agrícolas y permite aprove- char información generada previamente en zonas donde se cuenta con información de suelos. Den- tro del contexto actual del sector agropecuario, se recomienda la utilización de los MDS, como una alternativa confiable para generación de datos y su análisis, para el recurso suelo.