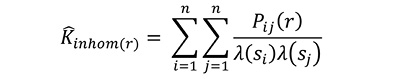Spatial patterns and interactions play a central role in many ecological theories of biological communities and populations (Legendre & Fortín, 1989; Dale, 1999; Condit et al., 2000). Knowledge of these patterns and interactions allows understanding of the ecological processes of spatiotemporal structuring of tropical forests (Fangliang, Legendre, & Lafrankie, 1997; Batista & Maguire, 1998; Silva et al., 2014; Rockwell et al., 2017), becoming essential for the developing strategies for conservation and management of tree species in the long-term (Myster & Malahy, 2012).
In tropical forests, several mechanisms contribute to aggregation of tree species, such as segregation of specific niches (Pielou, 1961), habitat heterogeneity (Harms, Condit, Hubbell, & Forster, 2001), dispersal limitations (Hubbell, 2001), reproductive behavior, and type of predation (Janzen, 1970). The regular spatial patterns derive from the interaction between individuals, being less common in plant populations and communities (Fangliang, Legendre, & Lafrankie, 1997), but found in allelopathic species that present biological inhibition or in environments with limited resource availability, where competition is intense due to the sites saturation (Silva, Martins, Santos, & Ribeiro, 2009).
Random patterns represent the null hypothesis of most models described in the form of a point spatial process. In natural forests, the occurrence of this pattern implies in environmental homogeneity or lack of habitat specificity of the species (Matteucci & Colma, 1982), and may be a consequence of antagonistic pressures such as illegal logging (Ricklefs & Miller, 2000). Thus, several factors that influences the spatial distribution of tropical trees can be synthesized under two main effects: 1) first-order effects, which are global and of large scale, reflecting abiotic characteristics; and 2) second-order effects, which derive from the spatial dependence of a small-scale process, resulting from biotic interactions (Bailey & Gatrell, 1995; Pottker, Oliveria, Figuereido, & Dalmaso, 2016).
In plant communities, trees interact under diverse ways, making it easier or more difficult for the establishment of other trees (Callaway, 1995; Ewel & Hiremath, 2005; Volkov, Banavar, & Hubbel, 2009). Positive interactions have been investigated in several ecological systems, aiming mainly understanding the facilitation mechanisms (Callaway, 1995). On the other hand, negative interactions usually derive from competition and allelopathy (Connell, 1983; Crawley, 1986). These two types of interactions can bring spatial patterns of attraction or repulsion, which, once quantified, provide important evidence about the spatiotemporal dynamics of plant populations and communities (Callaway, 1995; Chen & Bradshaw, 1999; Condit et al., 2000).
This study aims to investigate the spatial patterns and interactions of three dominant tree species in a Brazilian Amazon tropical rainforest, considering the effects of first- and second-order factors. Thus, we formulated the following questions: How are these species spatially distributed in the study area? Do the species have spatial patterns and interspecific interactions dependent on scale? Can spatial interactions between dominant trees in high-diversity forests be explained by overlap or segregation of habitats?
Material and methods
Study area: This study was carried out in Jamari National Forest (Jamari FLONA), located in Rondônia State, North Brazil, between geographical coordinates (09º00’00’’- 09º30’00’’ S & 62º44’05’’- 63º16’64’’ W). The climate of the region is rainy tropical, type Aw (Köppen), with a dry period well defined in the winter season and average annual precipitation around 2 400 mm (Alvares, Stape, Sentelhas, de Moaes Gonçalves, & Sparovek, 2013). Dense and open tropical rainforest typologies predominate in the region.
Flona do Jamari was the first public forest in Brazil to adopt the governments’s system of forest concession for lumber production through Sustainable Forest Management (Bauch, Sills, Rodríguez, Mcginley, & Cubbage, 2009). The said forest is characterized by large diversity and richness of species with commercial size which occupy the upper levels and clear dominance of some lumber species (Péllico Netto, Pelissari, Cysneiros, Bonazza, & Sanquetta, 2017).
Database: We used an unlogged Production Unit to evaluate the patterns and special interactions of dominant species under natural conditions, in the forest, without interventions. We used populations data of the following timber species: Astronium lecointei Ducke (Anacardiaceae), with 1 296 trees; Dinizia excelsa Ducke (Fabaceae), with 986 trees; and Peltogyne paniculata Benth. (Fabaceae), with 1 598 trees. Data were obtained from forest census of 1 596 ha, carried out in the year 2015, where 17 551 trees with DBH (Diameter at Breast Height) ≥ 40 cm (1.3 m above the ground) were measured. All trees were botanically identified and spatially located by means of geographical coordinates obtained with GPS Garmin 60s.
The selected species are dominant on studying area, presenting the highest values of importance in the forest (Péllico Netto et al., 2017). These species are widely traded in Amazon region due to characteristics that suit the tropical timber market (IBAMA, 1997; Ferreira & Hopkins, 2004; Rivera-Martín, Peñuela-Mora, Rojas, & Jaramillo, 2013). As common features, these species have predominantly wind dispersal syndrome and occur in “terra-firme” forests, grown under nutrient-deficient soils (Oliveira & Mori, 1999; Ribeiro et al., 1999; Ferraz, Leal Filho, Imakawa, Varela, & Piña Rodrigues, 2004; Laurance et al., 2004), being often cited as the largest trees in the Amazon forest (Guillaumet, 1987; Oliveira & Mori, 1999).
Astronium lecointei has irregular fruiting, with numerous fruits, which are small and easily dispersed by wind (Ferraz et al., 2004); it is cited as the highest species in the studying area (Cysneiros, Pelissari, Machado, Figueiredo Filho, & Souza, 2017). Dinizia excelsa fruits are indehiscent, measuring up to 35 cm in length, with the wind and gravity acting on the primary dispersion, where most of the seeds are lost while still green due to the attack of parrots and monkeys (Dick, Etchelecu, & Austerlitz, 2003). The fruits of Peltogyne paniculata are dehiscent, measuring up to 5 cm in length, which, due to animal predation, adopt a high seed production as regeneration strategy, where barochoric and zoochoric dispersion may occur (Rivera-Martín et al., 2013).
Data analysis: To verify possible influences of first-order factors on the species distribution, density maps were constructed used the Kernel estimator (Pottker et al., 2016). Inhomogeneous Ripley’s K-function was used for the spatial distribution patterns analysis of the species by means of second-order factors (Baddeley, Moller, & Waagepetersen, 2000), considering a 250 m influence radius, through estimator and edge correction presented by Ripley (1977). This function was applied for data and non-stationary process, common in natural forests where the tree species presents intense spatial variability (Baddeley et al., 2000; Baddeley & Turner, 2005; Pottker et al., 2016).
Where: = inhomogeneous K-function; indicator function; λ = first-order intensity of the events and ; and r = distance vector.
K-function has as main advantage the possibility of evaluating the spatial patterns of a series of points in different scales, varying the radius of the formed circles (Batista & Maguire, 1998; Capretz et al., 2012). This function considers as null hypothesis (H0) the complete spatial randomness (CSR) of a series of points. Thus, the spatial pattern is classified as random, if the observed values () are within the limits of the reliable envelopes; aggregate, when outside the reliable envelopes and with positive values; and regular, when outside the envelopes and with negative values (Batista & Maguire, 1998; Capretz et al., 2012).
K-function is described by a simple quadratic equation (K (r)), although its transformation to linear form () results in variance stabilization and better graphic interpretation of spatial patterns (Batista & Maguire, 1998). A total of 1 000 Monte Carlo simulations were used for construction of the envelopes (α = 0.01). For this, the analyses were performed in R 3.3.2 program (R Core Team, 2017) with the Spatstat package (Baddeley & Turner, 2005).
Statistics derived from the inhomogeneous K-function in its bivariate form (Kcross.inhom) were used to assessment of spatial interactions (Baddeley et al., 2000). This function is a generalization of the function Kcross to include an adjustment for spatially inhomogeneous intensity, similar to function Kinhom (Moller & Waagepetersen, 2003). Species density maps were made by Kernel estimator in raster format and submitted to correlation tests to verify the overlap or segregation of habitats. Thus, the influence of habitat on species spatial interactions of the species was verified.
Results
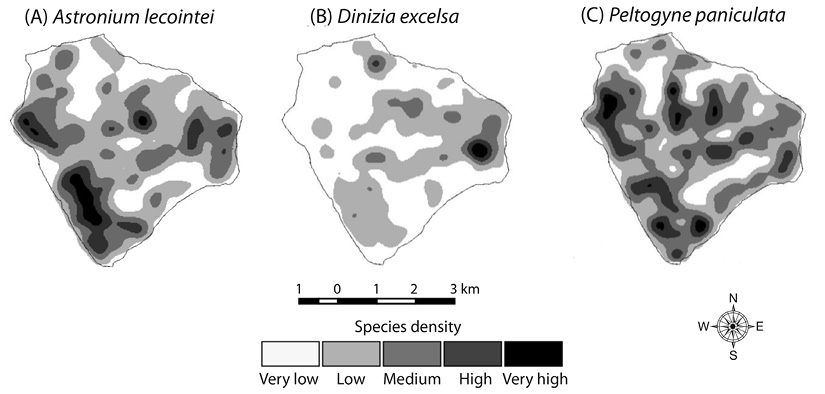
Spatial distribution: The species presented distinct spatial patterns, with visible separation between the nuclei of greater density and aggregation (Figure 1). Density map of Astronium lecointei showed highest concentration of high- and very high-density classes in the Western and Southern portions. For Dinizia excelsa, a greater area extension was observed for the low- and very low-density classes, with the highest density in the East portion, whereas for Peltogyne paniculata, a high fragmentation of density classes was noted along of the study area surface.
Confidence envelopes evidenced distance-dependent spatial patterns generated by second-order factors (Figure 2). The species Astronium lecointei presented aggregation at distances (r) close to 50 y 120 m. On the other hand, Dinizia excelsa had spatial randomness for all the analyzed distances, while Peltogyne paniculata showed a greater aggregation in relationship to the other species, with significance of the aggregate pattern of 10 m to 120 m distance.
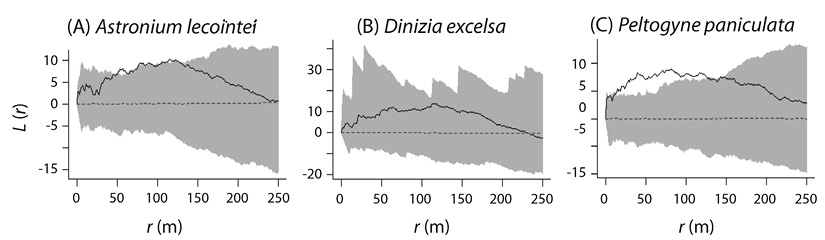
Figure 2 Confidence envelopes generated by the inhomogeneous K-function for the study species populations, where: L = univariate inhomogeneous K-function in linear form, and r = distance vector in meters.
Spatial interactions: The analysis of the interspecific spatial associations of the three dominant species indicated the occurrence of weak and statistically non-significant interactions (α = 0.01). When comparing the population of Dinizia excelsa with the other species (Figure 3A, Figure 3C), negative interactions were more expressive, although not significant. Significance was only obtained between Astronium lecointei and Peltogyne paniculata at distances less than 75 m (Figure 3B). The positive and significant interaction indicates a tendency of attraction between the populations, providing evidence on the proximity of niches of these species.
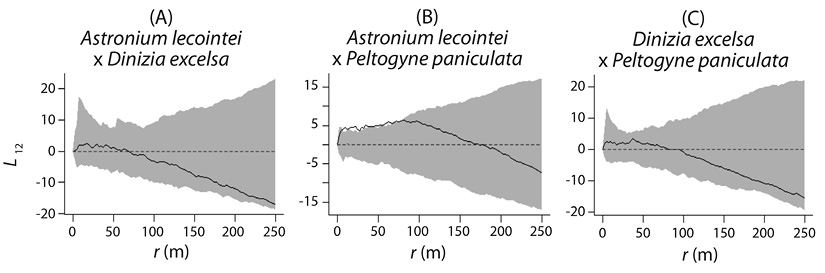
Figure 3 Confidence envelopes generated by the bivariate inhomogeneous K-function to analyze interspecific population interactions, L12 = bivariate inhomogeneous K-function in linear form.
A strong positive correlation was obtained between density maps of the species Astronium lecointei and Peltogyne paniculata (0.762), indicating the overlap of their habitats. On the other hand, Dinizia excelsa species showed a weak correlation with Astronium lecointei (0.321) and Peltogyne paniculata (0.385), suggesting a separation between habitats of these species or distinct preferences by environmental conditions.
Discussion
Spatial distribution - First-order factors: Spatial differences in the dispersion and aggregation of species can be explained by first-order factors. Astronium lecointei species is generalist regarding soil and topography (Figueiredo, Venticinque, Figueiredo, & Ferreira, 2015), and it occurs in the studied area in aggregated form and widely distributed. Likewise, Peltogyne paniculata frequently appears in inland forests (Ribeiro et al., 1999), of nutrient-poor and sandy soils (Laurance et al., 2004), which are predominant characteristics in the study area, providing formation of dense and widely distributed clusters. With an incidence restricted to plateaus and clayey soils (Ribeiro et al., 1999; Mesquita, Ferraz, & Camargo, 2007), Dinizia excelsa showed the lowest dispersion in the area, with few aggregation nuclei, indicating a possible influence of the habitat specificity in its distribution.
Spatial distribution - Second-order factors: The spatial aggregation pattern found for Astronium lecointei and Peltogyne paniculata is predominant for tropical trees (Hubbell, 1979; Fangliang et al., 1997; Condit et al., 2000; Lan et al., 2012; Rockwell et al., 2017). This pattern seems to be related to the autecological characteristics of the species on a local scale (Réjou-Méchain et al., 2011) and may be a consequence of the dispersal limitation (Condit et al., 2000; Seidler & Plotkin, 2006).
An explanation for aggregate spatial patterns derived from second-order factors is related to biotic features, such as dispersal syndrome and limitation (Seidler & Plotkin, 2006). This explanation is confirmed by comparing the two aggregate species of the present study, since the characteristics of the dispersal syndrome of Astronium lecointei favor its greater dispersion in the forest, reducing, therefore, the aggregation in relation to Peltogyne paniculata (Condit et al., 2000; Thomson, Moles, Auld, & Kingsford, 2011).
For Dinizia excelsa, other processes seem to influence the random pattern derived from second-order factors, since according to Odum (2010) this pattern can occur due to multiple local factors, such as the light requirement of the species, which grows in open areas (Dick, 2001). Due to the need for areas with a high incidence of light, the species depends on the opening of natural clearings to settle in dense forests, the occurrence of which may be spatially conditioned to random factors (Dick, 2001; Asner et al., 2013), thus resulting in the random pattern for the adult trees of the species.
Spatial interactions among populations: Negative interactions among tree populations are similar to competition among species, where the probability of occurrence of a species decreases with increasing abundance of antagonistic species (Volkov et al., 2009). Positive interactions suggest facilitating associations between individuals, with increased probability of occurrence of a species close to a facilitating species (Lan et al., 2012), while the absence of interactions between species is related to niche overlap, suggesting that the trees can share the same space (Higuchi, Silva, van den Berg, & Daniel, 2011).
In natural forests, positive interactions prevail over negative ones, indicating that this type of association has an important effect on the assemblages of forest species (Callaway, 1995; Lan et al., 2012; Luo, Yu, Chen, Wu, & Ding, 2012). The evidence of associations between species is best presented at smaller scales, where a high number of positive interactions can be found (Lan et al., 2012). However, the chance of two species interacting reduces when species richness in a community is high (Volkov et al., 2009; Luo et al., 2012). This finding is emphasized by the fact that interspecific relationships are weaker than intraspecific ones in tropical forests (Volkov et al., 2009). In these forests, the decline in associations for mature trees is expected due to local competition (Lan et al., 2012). Therefore, as a mature forest with high species diversity (Péllico Netto et al., 2017), the relationship between adult trees in the study area is less evident, confirming the results found.
Interspecific spatial attraction observed between Astronium lecointei and Peltogyne paniculata at short distances (< 75 m) can be explained by the ecological characteristics of the species, such as microhabitat preference (Wright, 2002; Luo et al., 2012). For tropical trees, partial overlap and segregation increase together with the spatial scale, where species with the same habitat preference tend to associate more frequently at small scales (Luo et al., 2012), suggesting that these species have the same preference for microhabitats. Kernel estimator confirmed the similarity in preferred microhabitats, indicating the overlapping of areas of higher concentration and density of the two species in some places.
The absence of significant interactions for Dinizia excelsa suggests that this species has a preferential habitat which differs from that of Astronium lecointei and Peltogyne paniculata, even though the absence of interactions indicates niche overlap (Higuchi et al., 2011), since trees with similar habitat preference tend to interact (Luo et al., 2012). This finding is reinforced by Kernel estimator, which indicated spatial differences for Dinizia excelsa in relation to the other two species, mainly with respect to areas of higher concentration and density.
Although not significant, the negative interactions of Dinizia excelsa with the other species may evidence the existence of local factors that cause spatial repulsion, such as competition (Connell, 1983; Ewel & Hiremath, 2005; Volkov et al., 2009). Cited among the Amazon tree species with higher biomass production (Guillaumet, 1987; Oliveira & Mori, 1999), Dinizia excelsa has a high growth rate (Mesquita et al., 2007) and a large crown that can shade large areas. Astronium lecointei and Peltogyne paniculata need shade in the early stages of life, with an increased need for light throughout their development (Ferraz et al., 2004; Rivera-Martín et al., 2013). These characteristics contribute to the repulsion generated by Dinizia excelsa, which, because of its dense and sparse crown, has an advantage in the competition for light and space, mainly with smaller light-demanding species.
Kernel estimator shows an influence of first-order factors on larger scales, indicating preference, overlap or segregation of niches and habitats. In addition, the inhomogeneous K function evidenced the influence of second-order factors on smaller scales, such as dispersion and competition for resources, with significance of patterns and interactions only at short distances. Different patterns and spatial interactions were observed for dominant tropical trees - depending on species and scale. The aggregation pattern found for A. lecointei and P. paniculata is related to ecological characteristics, such as preferential habitat and dispersal limitation. On the other hand, the random pattern found for D. excelsa is explained by specific features of its establishment, such as the need for clearings due to its light requirement. Considering the interspecific associations of the three species, spatial attraction results from the same preference for microhabitats and repulsion is a consequence of niche segregation.












 uBio
uBio