Geometría dinámica y proceso de argumentación

De acuerdo con el National Council of Teachers of Mathematics ^{(NCTM, 2000}), las tecnologías son esenciales para enseñar, aprender y hacer matemáticas; sin embargo, estas no deben ser utilizadas como un remplazo del profesor ni de los conocimientos matemáticos a enseñar. En el proceso de instrucción, las tecnologías juegan un rol de mediador semiótico para favorecer y propiciar un aprendizaje significativo (^{Bussi y Mariotti, 2008}; ^{Mejía y Molina, 2013}; ^{Radford, 2006}). En particular, el SGD GeoGebra integra herramientas del álgebra y cálculo, y permite abordar la geometría desde un ambiente dinámico. Además, a través de las diferentes vistas, es posible representar familias de objetos geométricos mediante la experimentación, manipulación y visualización; esto permite al alumno reforzar los significados generados a través de las construcciones geométricas y desarrollar un proceso de metacognición (^{Lagrange, Artigue, Laborde y Trouche, 2003}). En el estudio realizado por ^{Sandoval (2009}) con alumnos de 15 y 18 años, se muestra que el uso adecuado del software de geometría dinámica puede ayudar a descubrir y construir nuevos esquemas de uso, llegando a ser una herramienta mediadora entre el conocimiento perceptivo y el geométrico. Sin embargo, resalta que en este desarrollo es fundamental el papel del profesor. ^{Arcavi y Hadas (2000}) refieren a identificar un ciclo que ocurre cuando se utiliza la geometría dinámica en tareas matemáticas, el cual conforma la visualización, experimentación, sorpresa y retroalimentación; estos aspectos constituyen diversas habilidades de construcción, exploración y manipulación, donde el proceso de argumentación es relevante para el cierre del ciclo. Por tanto, el aprendizaje del alumno es favorecido al justificar y argumentar situaciones que involucran la exploración, manipulación y construcción mediante el SGD.

En este sentido, algunos autores han indagado en el proceso de argumentación en alumnos (^{Fiallo y Gutiérrez, 2007}; ^{Lara y Samper, 2014}; ^{Mariotti y Goizueta, 2018}; ^{Pedemonte, 2007}) como parte esencial de la actividad demostrativa. De estos estudios se rescata que para que los alumnos desarrollen un proceso de argumentación, se requiere madurez matemática durante la justificación de conjeturas en la solución de un problema. Por otro parte, en el contexto escolar el proceso de argumentación dista de la demostración formal y rigurosa, ya que, por su relación con estructuras axiomáticas, los alumnos manifiestan dificultades al aplicar propiedades que implican un razonamiento deductivo ^{(Fiallo, Camargo y Gutiérrez, 2013}; ^{Goizueta, 2015}). Además, el proceso de argumentación matemática está estrechamente relacionado con la validación de conjeturas, justificaciones, procedimientos y resultados, con el fin de desarrollar un razonamiento deductivo que contribuya al desarrollo de la demostración formal (^{Larios, 2015}).

Teselados o recubrimientos en el plano

Un referente sobre los teselados o recubrimientos en el plano es el artista holandés Maurits Cornelis Escher, quien analizó patrones de mosaicos de La Alhambra en Granada, España, lo que le llevó a realizar trabajos importantes referente a las isometrías en el plano, la geometría hiperbólica, los cuerpos platónicos, etc. Por otro lado, Kepler, al realizar un estudio de teselaciones, intentó explicar la armonía del universo y sus manifestaciones en términos geométricos, y afirmaba que los polígonos regulares eran figuras armónicas y perfectas ya que, al unir los ángulos interiores de cada polígono en un vértice sin dejar espacio o hueco entre ellos, se forma una congruencia en el plano.

En concreto, un teselado es un recubrimiento del plano con figuras poligonales que no se superponen ni dejan regiones sin recubrir. Existen diversos teselados en el plano, algunos de ellos son regulares y otros son semirregulares. Los primeros se construyen con regiones poligonales regulares congruentes, mientras que los semirregulares son los que se forman por dos o más regiones poligonales regulares (cada una de ellas congruentes entre sí).

En este estudio, los teselados o recubrimientos en el plano son el escenario por el cual se tiene acceso al estudio de las isometrías o trasformaciones isométricas (traslación, rotación, reflexión o simetría axial), a través del uso de herramientas propias de la geometría dinámica, particularmente, el software GeoGebra.

Prácticas matemáticas y configuraciones ontosemióticas

El enfoque ontosemiótico del conocimiento y la instrucción matemáticos (EOS) articula nociones institucionales y personales del conocimiento matemático en los procesos de enseñanza y aprendizaje (^{Godino, Batanero y Font, 2007}). Desde esta perspectiva, todas la acciones operativas y discursivas descritas por un sujeto; es decir, todo lo que puede hacer y decir referente a un objeto matemático (p. ej.: tipo de lenguaje; verbal, simbólico, gráfica, numérica, etc., propiedades, conceptos, argumentos y procedimientos) se le llama prácticas matemáticas^{(Godino y Batanero, 1994}). Las prácticas matemáticas son relativas al sujeto que las realiza; si son desarrolladas por una persona, se les llama prácticas matemáticas personales; si el sistema de prácticas al resolver un campo de problemas es compartido por una comunidad, son llamadas prácticas matemáticas institucionales (^{Godino et al., 2007}; ^{Godino, Font, Wilhelmi & Lurduy, 2009}).

En las prácticas operativas y discursivas que realiza un alumno durante la solución de un tipo de problema emergen conceptos, representaciones gráficas, simbólicas o algebraicas, propiedades, procedimientos y argumentos, a los cuales en el EOS se reconoce como objetos matemáticos primarios y que interactúan formando una red denominada configuración ontosemiótica. Esta noción permite describir, de manera sistémica, los objetos matemáticos intervinientes y emergentes en la práctica matemática (^{Gordillo y Pino-Fan, 2015}) y así se convierte en una herramienta potente para analizar a detalle la actividad matemática que desarrolla el individuo y los procesos de instrucción.

Las configuraciones ontosemióticas pueden ser epistémicas o cognitivas. Las configuraciones cognitivas se asocian al significado del alumno a través de la red de objetos matemáticos intervinientes y emergentes en el desarrollo de su práctica matemática. En cambio, las configuraciones epistémicas se asocian al significado institucional movilizado a través de la red de objetos matemáticos institucionales o por algún representante de este (^{Font y Godino, 2006}). En este estudio, la configuración epistémica se utiliza para analizar a priori las actividades propuestas, donde la argumentación matemática es vinculada a los esquemas de argumentación; mientras que la configuración cognitiva, para describir los significados de los alumnos a través de sus argumentos referentes a las situaciones propuestas.

Esquemas de argumentación

Las acciones operativas y discursivas que realiza el alumno cuando resuelve situaciones problemas que involucran el uso de la geometría dinámica incluyen acciones de construcción, experimentación, manipulación, validación, planteamiento de conjeturas y justificación, los mismos que forman parte de la práctica argumentativa. De acuerdo con ^{Morales, Rubio y Larios (en prensa}), la práctica matemática (operativa o discursiva) se asocia con la práctica argumentativa, cuando el alumno responde una situación problema que requiere de una justificación, validación, descripción, explicación, argumentación o demostración en el proceso de solución del problema, en el que puede o no manifestar un razonamiento lógico-deductivo.

Se pone atención en la justificación como parte del proceso de argumentación matemática. De acuerdo con ^{Flores (2007}), el conjunto de acciones y razonamientos que un individuo pone en juego para justificar y explicar un resultado o validar una conjetura que emerge de la situación problema se denomina esquema de argumentación. Dicho autor, al realizar un estudio con profesores de bachillerato, identificó esquemas de argumentación al resolver tareas que involucraron la geometría dinámica en el desarrollo de la práctica argumentativa. En este estudio, los esquemas de argumentación permiten clasificar las respuestas o argumentos manifestados por los alumnos, cuando desarrollan actividades mediante el uso del software GeoGebra. A continuación, se describen los esquemas de argumentación propuesto por ^{Flores (2007}):

En este estudio el esquema de argumentación autoritario no se considera, ya que las situaciones propuestas están pensadas para que los alumnos justifiquen y argumenten sus respuestas.

Participantes y contexto

El estudio se realizó con un grupo de 32 estudiantes (edades entre 15 y 18 años) que cursaban la asignatura de geometría analítica correspondiente al tercer semestre y al segundo ciclo escolar 2018 (agosto-diciembre), en la escuela de bachilleres de la Universidad Autónoma de Querétaro (UAQ). Por otro lado, con el fin de dar a conocer el objetivo del estudio y el tratamiento de los datos recabados, se realizó el procedimiento de consentimiento informado a los tutores responsables de los alumnos, ya que el investigador era ajeno a la institución. Las actividades propuestas en este estudio se desarrollaron en el laboratorio de matemáticas de dicha institución y en horario de clases de los alumnos correspondientes, aquí se exponen 4 de las 13 sesiones de 50 minutos cada una, por ser las sesiones que abordaron la actividad correspondiente a la construcción de teselados semirregulares. Además, fue necesario el uso de computadoras y del software de geometría dinámica GeoGebra, por lo que previo a la implementación de actividades, el investigador se aseguró de contar con dicho software. Dado que el número de computadoras fue insuficiente, se optó por desarrollar las actividades en parejas, formándose 16 de ellas. Por otra parte, el papel del investigador fue del tipo observador participante, ya que fue quien guio y monitoreó el desarrollo de actividades, en particular, se enfocó en atender dudas relacionadas con la comprensión de las situaciones propuestas en la actividad y el uso del software GeoGebra, ya que la mayoría de los alumnos contaban con poco conocimiento de las herramientas específicas a utilizar.

Instrumentos de recolección de datos

Los instrumentos para la recolección de datos consistieron en hojas de trabajo (actividades) y archivos dinámicos del GeoGebra, relacionados con el protocolo de construcción de los teselados semirregulares realizados por los alumnos de este estudio. Además, se realizaron notas en relación con la interacción expuesta entre las parejas de estudiantes cuando manifestaron sus argumentos.

La articulación del EOS con la ingeniería didáctica

Para el desarrollo de este estudio se utilizaron las fases de la ingeniería didáctica (ID) entendida como una clase especifica de la investigación basada en el diseño, tomando como base las herramientas teórico-metodológicas del EOS (^{Godino, Rivas, Arteaga, Lasa y Wilhelmi, 2014}). Este enfoque se centra en la búsqueda de conocimientos sobre cómo se construye y se comunica el conocimiento matemático, es decir, identificar pautas que orienten el diseño instruccional. Las fases que se distinguen son: estudio preliminar, diseño de experimento, implementación y evaluación o análisis retrospectivo. A continuación, se describen las fases de la ID en términos del EOS:

El estudio preliminar constituye un significado de referencia del contenido en relación con las acciones operativas y discursivas que sirven para identificar el significado pretendido durante el proceso de instrucción. Esta fase se asocia a la solución experta de cada actividad, muestra solo algunas situaciones. El diseño de experimento corresponde a la selección, secuenciación y análisis a priori de las situaciones problemas a desarrollar en el proceso de instrucción. En esta fase se describe el propósito y el tipo de situaciones propuestas, así como el análisis a priori de cada actividad a través la configuración epistémica de los objetos matemáticos intervinientes y emergentes. La implementación corresponde a la observación de interacciones entre los individuos y los recursos implementados. En esta fase se analizan y clasifican los argumentos manifestados por los alumnos de este estudio mediante los esquemas de argumentación y la configuración cognitiva en relación con los argumentos. La evaluación o análisis retrospectivo consiste en una valoración o contraste entre lo previsto en el diseño y lo observado durante la implementación. Esta fase corresponde a la valoración del análisis a priori y a posteriori de las configuración epistémica y cognitiva. Así como la reflexión sobre el diseño que incorpora el uso de un SGD.

Diseño de actividades y estudio preliminar

En este apartado se abordan las dos primeras fases de la ingeniería didáctica, donde el contenido en estudio se sitúa en el contexto de los teselados, como un medio de aplicación de las transformaciones isométricas en el plano. Dado que el interés fue identificar y describir los argumentos manifestados por los alumnos de este estudio, con el fin de conocer cómo argumentan cuando utilizan el software GeoGebra, el diseño consistió en una secuencia de cinco actividades centradas en el planteamiento de preguntas abiertas (situaciones problema), las cuales se enfocaron en promover la argumentación matemática cuando se usa un software de geometría dinámica. Este diseño fue validado a través de tres expertos en el tema, teniendo como referencia la solución experta y un pilotaje previo.

El diseño de actividades también incluyó situaciones donde los alumnos no necesariamente tenían que usar el software, principalmente aquellas que abordaron los conocimientos previos; sin embargo, estas fueron necesarias para guiar y secuenciar el desarrollo de las actividades, donde la aplicación de las transformaciones isométricas fue primordial para lograr la construcción de los teselados regulares y semirregulares. Por cuestiones de espacio, en este estudio se enfatiza en la actividad que aborda la construcción de teselados semirregulares, la cual se eligió por ser la que integró la experiencia ganada por parte de los alumnos en una actividad previa, que abordó la construcción de teselados regulares y el uso de las transformaciones isométricas del GeoGebra.

El estudio preliminar se desarrolló en dos momentos: Por un lado, se realizó la solución experta de la secuencia de actividades con el fin de establecer un significado de referencia en relación con lo esperado en la práctica argumentativa de los alumnos. Asimismo, esta solución experta permitió validar el diseño de la secuencia de actividades tanto del contenido matemático como de las herramientas a utilizar del software GeoGebra. Por otro lado, se realizó el análisis a priori de cada actividad utilizando la configuración epistémica de las trasformaciones isométricas, que permite identificar la red de objetos intervinientes y emergentes. En la Tabla 1 se presenta el propósito de la cuarta actividad y la solución experta de las situaciones que la constituyen, las cuales se centran en la construcción y argumentación de teselados semirregulares (formados por dos o más polígonos regulares). Para el desarrollo de esta actividad se proporcionó el concepto de teselado semirregular, con el fin de que los alumnos tuvieran noción sobre este, y sugerencias de manera escrita y verbal para guiar al alumno a una apropiada aplicación de las herramientas del software GeoGebra.

Tabla 1: Propósito y solución experta de las situaciones referente a los teselados semirregulares 

Nota: Fuente propia de la investigación.

Dado que el énfasis se hace en la actividad que incorpora la construcción de teselados semirregulares (cuarta actividad), el respectivo análisis a priori se relaciona con los objetos matemáticos primarios (situaciones, elementos lingüísticos, definiciones, propiedades, procedimientos y argumentos) de la configuración epistémica de las transformaciones isométricas. En esta configuración, los argumentos se asocian a los esquemas de argumentación (fácticos, simbólicos, empíricos y analíticos), que se identificaron cuando los alumnos resolvieron las actividades. En la Tabla 2, se describe el análisis a priori correspondiente a la actividad que involucró la construcción de teselados semirregulares.

Tabla 2: Configuración epistémica de las transformaciones isométricas a través de los teselados 

Nota: Fuente propia de la investigación.

Análisis y resultados

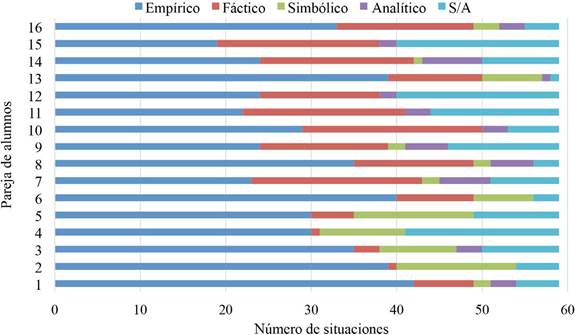
El propósito de este artículo fue identificar y describir los argumentos manifestados por los alumnos de este estudio en el contexto de los teselados cuando utilizan el software GeoGebra. Para ello, se realizó la clasificación de argumentos de los alumnos considerando los esquemas propuestos por ^{Flores (2007}), así como la configuración cognitiva para explicitar la red de objetos matemáticos intervinientes y emergentes en su proceso de argumentación matemática. La clasificación consistió en el análisis de 59 situaciones por pareja, teniendo un total de 944 respuestas o argumentos posibles de las 16 parejas. El 16 % del total se mostró sin argumento (S/A) debido a que no hubo respuesta o argumento por parte de los alumnos. Para el esquema de argumentación empírico se asoció a un 52 % de los argumentos, las parejas de alumnos basaron sus argumentos en describir el hecho físico (la construcción) en términos de las herramientas del GeoGebra, donde la percepción (visual) fue esencial para la exploración, manipulación y construcción. Sin embargo, este hecho no formó parte de un argumento razonado. El esquema de argumentación fáctico se identificó en un 20 % de los argumentos de las parejas de alumnos, ellos recurrentemente realizaron explicaciones a modo de secuencia de pasos, en particular, cuando realizaron las construcciones de los teselados y se les pedía explicar el proceso de construcción hecho en el software GeoGebra. El esquema de argumentación simbólico fue identificado en un 8 % de los argumentos de las parejas de alumnos, es decir, ellos utilizaron un lenguaje matemático poco apropiado y consistente al expresar y describir sus argumentos, más bien, usaron un lenguaje informal y afirmaciones escasamente argumentadas. Finalmente, el esquema de argumentación analítico se identificó escasamente, teniendo solo el 4 % de los argumentos manifestados por las parejas de alumnos. Este esquema se promovió cuando tenían que realizar exploración, manipulación o construcción, ya que sus argumentos tenían que ser justificados mediante los conceptos de las transformaciones isométricas y las herramientas correspondientes en el software GeoGebra. La Gráfica 1 muestra la clasificación antes mencionada, referente al número de situaciones que se analizaron por las 16 parejas en relación con los esquemas de argumentación.

Nota: Fuente propia de la investigación.

Gráfica 1: Esquemas de argumentación asociados a cada pareja de alumnos 

Para ejemplificar los esquemas de argumentación, se muestran las respuestas de la pareja 8, la cual se eligió por tener menor número de situaciones sin argumentos y más argumentos analíticos, aunque estos no necesariamente fueron evidenciados en la actividad correspondiente a la construcción de teselados semirregulares. Además, se presenta la configuración cognitiva asociada a las respuestas de esta pareja en relación con la construcción de teselados semirregulares, donde sus argumentos se asocian a los esquemas de argumentación identificados.

Esquemas de argumentación de la pareja 8

La primera situación mostrada en la Figura 1 se relaciona con el esquema analítico, la cual proviene de la exploración y manipulación de un applet que involucra la traslación geométrica de una figura. Por lo que la pareja 8 experimenta sobre forma, tamaño y orientación de la figura trasladada, eso le permitió determinar que la medida del vector representa una distancia entre figura trasladada y su preimagen. Sin embargo, para la segunda situación la pareja no asocia la respuesta anterior con la definición correcta de la traslación geométrica, de esta manera se identifica una discordancia entre el razonamiento deductivo a partir de la exploración y manipulación realizados en la primera situación y el poco dominio que se concibe en relación con el concepto de la traslación.

Figura 1 Esquema de argumentación analítico de la pareja 8. 

La situación mostrada en la Figura 2 está asociada a la manipulación de polígonos regulares realizada por los alumnos mediante un deslizador que representa diferentes medidas de ángulos asociados a polígonos regulares en el GeoGebra. El argumento manifestado en esta situación por la pareja 8 corresponde a un esquema de argumentación simbólica, ya que, aunque la respuesta es correcta, por relacionar de manera ostensiva el concepto de ángulo llano, cuando este se forma entre dos semirrectas de la misma pendiente y comparten un mismo vértice, hay inconsistencia al decir que la figura sería plana y recta.

Figura 2 Esquema de argumentación simbólico de la pareja 8. 

El argumento de la pareja 8 en la Figura 3 se asocia al esquema de argumentación empírico. Este argumento se basa en un hecho físico que los alumnos representan a través de un dibujo y al conjeturar que la suma de ángulos en cada vértice es 360°, para posteriormente reproducir en el GeoGebra. Además, este argumento desprende una conjetura referente al cálculo de la suma de ángulos en cada vértice, esto a partir del hecho de dibujar triángulos y cuadrados para determinar que estos polígonos formarían un teselado semirregular.

Figura 3 Esquema de argumentación empírico de la pareja 8. 

El argumento de la pareja 8 en la Figura 4 corresponde al esquema de argumentación fáctico, recurren a una serie de pasos a manera de explicación de un procedimiento de construcción geométrica, cuando aplican la herramienta de polígono y traslación del GeoGebra. El argumento carece de una explicación detallada en términos de cada una de las herramientas aplicadas del software, cuando ampliaron el teselado semirregular. Por ejemplo, no refieren dónde ubicaron el vector de traslación, ni cómo fue que “copiaron la figura” para generar el teselado. De acuerdo con el protocolo de construcción, los vectores no se ubicaron sobre los polígonos base y la traslación se aplicó a un conjunto de polígonos, en vez de uno a uno. Por lo que al validar la construcción del teselado aplicando la herramienta de “arrastre”, este no cumplió con la definición de teselado semirregular.

Figura 4 Esquema de argumentación fáctico de la pareja 8. 

En este estudio la configuración epistémica y cognitiva representan el análisis a priori y a posteriori en relación con la construcción de los teselados semirregulares. En la Tabla 3, se muestran los significados personales de la pareja 8 en relación con la red de objetos intervinientes y emergentes. Referente a los conceptos, la traslación se planteó de manera parcial, pero no es aplicado de manera correcta en el GeoGebra. Además, la definición del teselado semirregular no es considerada al justificar el proceso de construcción del teselado. Respecto a las propiedades de los teselados, estos fueron validados mediante la prueba de “arrastre”; sin embargo, la pareja 8 solo aplicó está herramienta porque se indicaba en la actividad y en las sugerencias, y perdió de vista que tenían que usarse para validar la construcción correcta del teselado. Además, solo se tomó en cuenta que no hubiera espacio entre los polígonos, sin argumentar que la medida de la suma de ángulos en cada vértice del teselado debiera ser de 360°. Los procedimientos fueron poco detallados y estructurados, pues, aunque se aplicó la herramienta de traslación, está no fue usada correctamente y tampoco se utilizó para explicar a detalle el procedimiento realizado en la construcción del teselado. Mientras que los argumentos asociados corresponden con los esquemas previstos en la configuración epistémica, el esquema epistémico y el fáctico son los más recurrentes por la pareja 8. Por ejemplo, al utilizar representaciones figurales para argumentar el tipo de teselado semirregular y que la medida de la suma de ángulos debiera ser 360° en cada vértice del teselado semirregular. Aunque aquí es utilizada esta propiedad, no es mencionada en el proceso de construcción. Los elementos lingüísticos utilizados fueron del tipo verbal e informal, en términos del uso de las herramientas del GeoGebra.

Tabla 3: Configuración cognitiva asociada a los teselados semirregulares de la pareja 8 

Nota: Fuente propia de la investigación.

Consentimiento informado

Los alumnos que participaron en este proyecto fueron informados sobre los alcances de su participación y se respetaron sus derechos a la privacidad y a retirarse del proyecto en el momento que así lo decidieran.

Declaración de la contribución de los autores

El porcentaje total de contribución para la conceptualización, preparación y corrección de este artículo fue el siguiente: G. M. R. 40 %, V. L. O. 30 % y N. R. G. 30 %.

Declaración de disponibilidad de los datos

Los datos que respaldan los resultados de este estudio serán puestos a disposición por el autor correspondiente (G. M. R.), previa solicitud razonable.