Introducción
El early algebra es una propuesta curricular que plantea la introducción de modos de pensamiento algebraico desde los primeros niveles educativos para favorecer el razonamiento matemático y mitigar las dificultades que encuentran estudiantes cuando abordan el álgebra en cursos superiores (Kieran, 2004), que es lo habitual en la gran mayoría de los países (Blanton, Brizuela, Gardiner, Sawrey y Newman-Owens, 2015; Morales, Cañadas, Brizuela y Gómez, 2018).
Entre los contenidos matemáticos que usualmente se trabajan en educación primaria y el tratamiento que se le da al álgebra en educación secundaria se produce un salto abrupto (Bednarz, Kieran y Lee, 1996; Filloy, Puig y Rojano, 2008). Este tratamiento del álgebra se caracteriza por ser formal y no prestar atención a nociones como la generalización y el razonamiento, lo cual motiva la propuesta early algebra (Molina, 2006). La generalización es un proceso esencial en el razonamiento matemático. Atenderla en los cursos más básicos permite, por ejemplo, que el estudiantado se aleje de las particularidades adheridas al cálculo aritmético, al poder identificar la estructura y las relaciones matemáticas involucradas (Blanton, Levi, Crites y Dougherty, 2011).
La propuesta del early algebra pretende promover un aumento de la capacidad para expresar la generalidad desde los primeros niveles educativos, a partir de la observación de patrones de comportamiento o regularidades desde unos casos particulares dados; consiste en una “algebrización del currículo” (Kaput, 2000).
Existen publicaciones que forman parte de grandes proyectos, en diferentes países, que ponen el énfasis en la evidencia de que la niñez, en los primeros niveles educativos, puede pensar de manera bastante más sofisticada de lo que se suponía (e.g., Kaput, Blanton y Moreno, 2008; Pinto y Cañadas, 2017a; Radford, 2018; Torres, Cañadas y Moreno, 2018; Vergel, 2015). Particularmente, la investigación evidencia que, aun cuando las producciones estudiantiles no contienen los signos alfanuméricos del álgebra, su pensamiento puede ser genuinamente algebraico (Vergel, 2014).
Este trabajo se centra en el pensamiento funcional, un tipo de pensamiento algebraico en el que la función es la noción matemática protagonista. “El pensamiento funcional se basa en la construcción, descripción, representación y razonamiento con y sobre (sic) las funciones y los elementos que las constituyen” (Cañadas y Molina, 2016, p. 3). “El pensamiento funcional, en el contexto del early algebra, se centra en la relación entre dos variables, siendo fundamental el estudio de regularidades y, en particular, su generalización” (Blanton, 2008, p. 30). De manera general, la regularidad es lo que se repite y, a partir de una regularidad observada, se prueba que esta sea válida para más casos particulares y, finalmente, para cualquier caso perteneciente a una situación dada (Pólya, 1966). Concretamente, en el contexto funcional, la estructura para referirse hace alusión a la regularidad que define las relaciones existentes entre las variables de una función. A través de la identificación de una estructura entre valores concretos de ambas variables (casos particulares), se puede llegar a generalizar siguiendo un proceso de razonamiento inductivo (Cañadas y Castro, 2007).
Cada función tiene dos formas que se denominan directa e inversa. El pensamiento funcional se centra en las relaciones, tanto directa (de la variable dependiente con la variable independiente) como inversa (en la que se intercambian los valores respecto a la relación directa), existentes entre cantidades que tienen capacidad de variación simultánea (Blanton y Kaput, 2004; Warren y Cooper, 2005). Pinto y Cañadas (2017a) exploraron cómo 24 estudiantes de quinto de educación primaria (10-11 años) identificaron la forma inversa de una función al trabajar con una tarea (y=2x+6). Concluyeron que 10 estudiantes establecieron diferentes estructuras que involucran las variables en la función inversa. Por otra parte, 5 estudiantes generalizaron esta forma de la función. Los autores encontraron que las respuestas son más coherentes y precisas en el estudio de la forma directa.
Diferentes investigaciones describen la generalización de estudiantes de educación primaria en contextos funcionales (e.g., Carraher y Schliemann, 2016; Pinto y Cañadas, 2017a), pero no hay estudios sobre cómo estudiantes de educación primaria identifican y generalizan las estructuras tanto en las formas directa e inversa de una función en edades tempranas. Nuestra investigación persigue identificar y comparar las estructuras que evidencian los estudiantes en las formas directa e inversa de una función, tanto para el trabajo con casos particulares como en la generalización. El grupo de estudiantes participantes en la investigación es de segundo de primaria (7-8 años) de un colegio de Granada (España).
Generalización y estructura en un contexto funcional
Pólya (1945) considera la generalización como una actividad empírica inductiva en la que se acumulan ejemplos concretos y se detecta y se sistematiza una regularidad. La generalización es una capacidad cognitiva que se puede desarrollar. Asumimos que generalizar es pasar de lo particular a lo general (Mason, 1996). Para Radford (1997) generalizar es observar algo que va más allá del dominio de unos casos particulares. La generalización es un elemento central del razonamiento inductivo y requiere de una abstracción a partir de casos particulares para extraer una conclusión (Driscoll, 1999).
En este estudio, nos aproximamos al álgebra desde una tarea de generalización en un contexto funcional, una de las vías que promueven algunos autores (e.g., Blanton y Kaput, 2004). La función es el contenido matemático presente en este contexto. Blanton, Brizuela, Gardiner, Sawrey y Newman-Owens (2015) caracterizaron diferentes niveles de sofisticación en el pensamiento de los niños y las niñas a través de trayectorias de aprendizaje al aplicar diferentes funciones en un estudio longitudinal. Los resultados sugieren que la niñez puede aprender a pensar de manera generalizada sobre las relaciones en los datos de funciones, más allá del enfoque curricular típico en los primeros cursos de primaria, donde se suele considerar una sola secuencia de valores.
Usualmente, se utilizan tareas de generalización que involucran una función lineal para promover el pensamiento funcional de estudiantes. En el proceso de generalización, ellos pueden identificar diferentes estructuras de la función involucrada en la tarea. En el ámbito del pensamiento funcional se habla de estructuras para referirse a la expresión de las regularidades presentes entre las variables de las funciones involucradas (Pinto y Cañadas, 2017a). Se explora cómo los estudiantes identifican las estructuras sin atender la posición ni el crecimiento, como sucede en el estudio de los patrones, sino atendiendo a la relación de covariación y a la generalización de esas estructuras. El estudio del patrón y la estructura está integrado en una amplia gama de estudios de desarrollo matemático en los primeros años de enseñanza (Mulligan y Mitchelmore, 2009). La idea de patrón se relaciona más con la noción de recurrencia que con la de estructura, ya que esta última está referida al establecimiento de una relación de covariación entre dos cantidades. Una de las manifestaciones del pensamiento funcional es a través del reconocimiento de una estructura. Para interpretar cómo los estudiantes identifican una estructura, se define, desde un punto de vista cognitivo, como la forma en la que es evidenciada la regularidad entre las variables (Pinto y Cañadas, 2017a). Esta regularidad puede ser expresada a través de diferentes representaciones, tanto al trabajar con casos particulares de las variables como al generalizar.
Diferentes estudios distinguen entre distintos tipos de generalización (e.g., Ellis, 2007; Radford, 2010). Dado que en este trabajo se plantean cuestiones siguiendo el modelo de razonamiento inductivo de Cañadas y Castro (2007), partiendo de casos particulares hasta llegar al caso general, se asume la distinción entre generalización espontánea e inducida establecida por Pinto y Cañadas (2017b). La generalización espontánea se produce sin preguntar explícitamente por ella y suele darse cuando se plantean cuestiones relacionadas con casos particulares. La generalización inducida se produce cuando se pregunta explícitamente por el caso general. Para generalizar, se debe identificar la estructura a partir de unos casos particulares. De esta manera, las nociones de generalización y de estructura están relacionadas. Esta última es útil para interpretar y presentar las producciones de los estudiantes sobre la relación que observan entre las variables involucradas en una tarea de generalización.
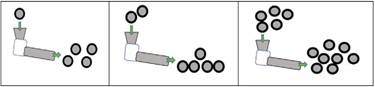
Torres, Cañadas y Moreno (2018) diseñan unas categorías sobre las estructuras evidenciadas por seis estudiantes de educación primaria de la forma directa de la función y=x+3 cuando trabajan con casos particulares y cuando trabajan con la generalización. La tarea de generalización con la que trabajaron consistía en una máquina en la que se introducían un número determinado de bolas y salían otro número concreto de bolas siguiendo la función mencionada, como se observa en los casos particulares de la Figura 1.
Los estudiantes identificaron cuatro tipos de estructuras diferentes (y=x+3, y=x+x, y=x+2, y=x+1), durante los casos particulares dados. La mayoría generalizó verbalmente la estructura correcta, y=x+3, al preguntar sobre la generalización, e identificaron la misma estructura para casos particulares y para el caso general, observándose coherencia en sus respuestas.
Los estudiantes de educación primaria pueden utilizar diferentes tipos de representaciones para expresar las estructuras que identifican en las tareas con funciones lineales. Estas incluyen (a) lenguaje natural - oral, (b) lenguaje natural - escrito, (c) pictórico, (d) numérico, (e) notación algebraica, (f) tabular y (g) gráfico (Carraher, Martínez y Schliemann, 2008). Asumimos que la representación verbal es aquella que se hace mediante el lenguaje natural, ya sea oral o escrito. La representación verbal y la pictórica resultan claves para el trabajo con estudiantes de los primeros cursos de educación primaria (Cañadas y Fuentes, 2015). La representación numérica es empleada junto a la verbal por estudiantes de educación primaria (Torres, Cañadas y Moreno, 2019).
Formas directa e inversa de una función
La función es una relación de covariación que se establece entre los valores de uno o más conjuntos de datos respecto de otro (u otros). En este trabajo nos centraremos en las funciones que relacionan dos variables que covarían (Thompson, 1994). Dada la edad de los estudiantes con los que trabajamos, nos ceñimos a las funciones lineales (y = mx+n, siendo m y n números naturales), con dominio y codominio también en los números naturales.
Se establecen dos relaciones en las funciones de dos variables: formas directa e inversa de la función. Merino, Cañadas y Molina (2013) trabajaron con la relación que se puede establecer entre el número de mesas y las personas que se pueden sentar alrededor de ellas. Definieron, en su investigación, como forma directa de la función, a aquella que, dado el número de mesas, permite conocer el número de niños que se pueden sentar a su alrededor. En cambio, cuando es conocido el número de niños que están sentados, y se requiere el número de mesas que son necesarias, la tomaban como la forma inversa de esa función.
Cuando hablamos de una función y = f(x), en general, se está haciendo referencia a su forma directa, pues es la manera usual en la que se representa la regularidad entre las dos variables en un contexto concreto. Esa función tiene una función inversa y = g(x), tal que g (f (x)) = f (g (x)) = x. En este estudio fijamos, de partida, una función dada y=x+4 que decidimos que es la que se refiere a la forma directa por considerarla más sencilla. Se afirma que, para los casos por los que preguntamos a los estudiantes, para uno o más valores de x, estaremos indagando sobre la capacidad del sujeto para identificar o generalizar la forma directa de esa función. Sin embargo, cuando se intercambian los roles de las dos variables en ese mismo contexto, entonces se está indagando sobre la capacidad del sujeto para identificar o generalizar sobre la forma inversa de esa función. La forma directa está determinada por la forma en la que se presentan los datos iniciales. En este estudio se tomará como forma directa de la función aquella que se supone más sencilla para los estudiantes.
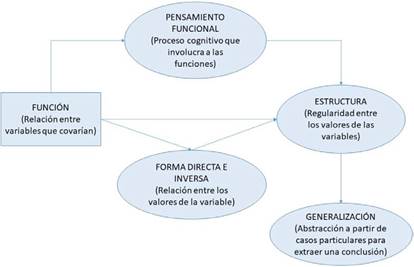
En la Figura 2 presentamos un mapa conceptual que incluye y relaciona los elementos teóricos de este trabajo. El sentido de las flechas recoge el camino hacia la generalización como culmen del proceso del pensamiento funcional manifestado.
La generalización es el resultado del proceso seguido. La posición que ocupan las formas directa e inversa en nuestro estudio es central (ver Figura 2), ya que permite explorar el pensamiento puesto en juego por los estudiantes en dos direcciones (directa e inversa). Las estructuras identificadas y expresadas por los estudiantes nos ayudan a conocer el pensamiento funcional con mayor profundidad. Para que haya evidencia de pensamiento funcional es necesario que esté implícita una relación, ya sea en la forma directa o inversa de la función. Para cada una de estas formas, atendiendo a la estructura identificada, se puede observar, si se aproximan a la generalizacin, y cómo.
Nuestro objetivo general de investigación es describir cómo los estudiantes de educación primaria (7-8 años) identifican las formas directa e inversa de una función en una tarea de generalización en un contexto funcional del early algebra. Para ello, se define el siguiente objetivo específico de investigación: identificar y comparar las estructuras que evidencian los estudiantes en las formas directa e inversa de una función, tanto en el trabajo con casos particulares como en el caso general.
Metodología
Llevamos a cabo un estudio cualitativo y de carácter exploratorio y descriptivo. Dentro del paradigma de la investigación de diseño, se desarrolla un experimento de enseñanza con sesiones de trabajo (Molina, Castro, Molina y Castro, 2011). Los experimentos de enseñanza son los estudios de diseño más frecuentes de la investigación de diseño (Castellanos, Flores y Moreno, 2018). Las sesiones del experimento constituyen el contexto previo a la realización de unas entrevistas semiestructuras. En la Tabla 1 se recogen los diferentes contextos y funciones lineales implicadas en la secuencia de sesiones que tuvieron lugar antes de la toma de datos que llevamos a cabo con las entrevistas.
Tabla 1 Características de las sesiones de clase
| Contexto | Función |
|---|---|
| Sesión 1: máquina de bolas | y = x+3 |
| Sesión 2: parque de atracciones 1º | |
| Sesión 3: parque de atracciones 2º | y = 2x+1 |
| Sesión 4: cumpleaños | y = 2x |
| Sesión 5: paradas de tren |
En las sesiones se aplicaron cuestionarios basados en tareas de generalización que consisten en obtener nuevos casos particulares, o el caso general partiendo de unos casos particulares conocidos. Para ello, los estudiantes han debido identificar una estructura en esos casos particulares dados. Es decir, se les pide que reconsideren los patrones como funciones (como relación entre dos variables). Esto a menudo implica generar una representación o registrar de algún modo los casos particulares para identificar la relación entre dos conjuntos de datos.
En la Figura 3, se presenta un ejemplo de cuestionario aplicado después de introducir la tarea en la sesión 1 y que nos sirvió para seleccionar a los estudiantes de la muestra de este estudio.
Los estudiantes no recibieron retroalimentación sobre sus respuestas. Al aula entraron tres miembros del equipo de investigación: la profesora-investigadora, una investigadora de apoyo y otro investigador que grabó con la videocámara.
Al final de las sesiones del experimento de enseñanza, se realizaron unas entrevistas finales a seis estudiantes. Los propósitos de las entrevistas fueron: (a) explorar cómo los estudiantes relacionan las variables involucradas y (b) identificar las estructuras en las respuestas de los estudiantes a los casos particulares y al caso general. Para alcanzar los objetivos de investigación, se describieron las estructuras identificadas tanto en la forma directa como inversa de la función (durante los casos particulares y el general) como también las generalizaciones expresadas, diferenciando si eran espontáneas o inducidas.
Participantes
Los participantes de este estudio fueron seis estudiantes de educación primaria (7-8 años), de España, a los que realizamos una entrevista individual semiestructurada. Sus conocimientos previos eran los siguientes: números del 0 al 399, comparación de números y operaciones de sumas y restas con llevadas. La característica fundamental de los participantes es que no habían recibido enseñanza previa en torno a tareas que involucraran alguna función lineal y la generalización antes de las sesiones del experimento. Se seleccionaron a estos estudiantes de un grupo de 24 al que aplicamos un cuestionario inicial (ver Figura 4) en la primera sesión del experimento. Las preguntas del cuestionario involucran la función y=x+3 (ver Figura 1) en una tarea de generalización contextualizada. Seleccionamos a seis estudiantes teniendo en cuenta las recomendaciones de la profesora en cuanto a sus logros de aprendizaje y según hubieran avanzado en el proceso de generalización. En la Tabla 2 resumimos esta información.
(ver Figura 1) en una tarea de generalización contextualizada. Seleccionamos a seis estudiantes teniendo en cuenta las recomendaciones de la profesora en cuanto a sus logros de aprendizaje y según hubieran avanzado en el proceso de generalización. En la Tabla 2 resumimos esta información.
Instrumento de recogida de información
Para fundamentar el diseño de la entrevista y guiar el proceso hacia la generalización se sigue, en este estudio, una adaptación del modelo de razonamiento inductivo de Cañadas y Castro (2007) que se presenta en la Figura 4.
Con los pasos descritos en el modelo se observa cómo los estudiantes, a partir de los casos particulares, logran identificar estructuras para luego poder generalizar. Cuando los estudiantes expresan una conjetura se interpreta las estructuras que evidencian. Algunos estudios usan el modelo de Cañadas y Castro (2007) para diseñar cuestionarios que indagan en el proceso de generalización de estudiantes de los primeros cursos de educación primaria (Morales, Cañadas, Brizuela y Gómez, 2018).
En la entrevista, se plantea una tarea que involucra una función lineal de tipo aditivo (y=x+4). Se trata de una función lineal, que es recomendada para trabajar con estudiantes de educación primaria (Carraher y Schliemann, 2016). Se usó la edad de dos superhéroes cuya diferencia son 4 años como contexto. El enunciado fue el siguiente: “Iron Man y el Capitán América cumplen años el mismo día. Cuando Iron Man cumplió 5 años, el Capitán América cumplió 9. Cuando Iron Man cumplió 7 años, el Capitán América cumplió 11”. Un miembro del equipo de investigación fue el entrevistador, quien comenzó presentando la tarea a los estudiantes. A continuación, les mostró casos particulares (no consecutivos para evitar la recursividad en las respuestas de los estudiantes) de la tarea y avanzamos inductivamente hacia la generalización. Cada entrevista duró 20 minutos, tiempo suficiente para que este no fuera una limitación para los estudiantes.
Las entrevistas estaban constituidas por dos partes. En la primera, se les plantearon preguntas sobre la forma directa de la función y en la segunda la inversa. El protocolo seguido en ambas entrevistas fue análogo. Comenzaron con preguntas sobre los casos particulares para, finalmente, preguntar por el caso general. El número total de casos particulares presentados o tratados durante la entrevista es diferente de unos estudiantes a otros dependiendo de sus respuestas. Después de los casos particulares, preguntamos por el caso general determinado por la pregunta: ¿Cómo le explicarías a un amigo qué ha de hacer para conocer la edad de uno de los superhéroes? (el superhéroe cambia en función de la forma de la función que se esté trabajando, directa o inversa).
El entrevistador formulaba las preguntas que los estudiantes debían responder mediante un protocolo de actuación, el cual comenzó por las preguntas en que se conocía la edad de Iron Man y se desconocía la del Capitán América, que consideraremos la forma directa de la función. Una síntesis se presenta en la Figura 5.
Análisis y resultados
Tras las entrevistas, se analizaron los datos partiendo de las categorías de Torres, Cañadas y Moreno (2018), basadas en las estructuras identificadas por los estudiantes. Las categorías distinguen entre estructuras dadas para los casos particulares (donde se sitúa el trabajo con casos particulares de las variables) y el caso general (donde se pregunta con la indeterminación de manera explícita). Se amplían aquí estas categorías para acoger las estructuras evidenciadas durante el trabajo de la forma inversa de la función. Se atienden, así, las estructuras evidenciadas en las formas inversa y directa de la función. Se consideró que un estudiante identifica una estructura cuando responde a dos o más cuestiones siguiendo la misma regularidad o se observa en la generalización. De esta manera se evidencia si un estudiante es consciente de lo que se repite y su respuesta no es por casualidad o por cálculos ante una determinada pregunta. Por otro lado, se considera el tipo de generalización expresada: inducida o espontánea.
Se presenta un resumen de resultados mediante tablas que complementamos con algunos ejemplos de las respuestas dadas.
Tabla 3 Estructuras identificadas en la forma directa de la función
| Estructura | |||
|---|---|---|---|
| Estudiante | Casos particulares | Caso general | Tipo de generalización |
| E1 | y=x + 4 | y=4x y=x + 4 | Espontánea e inducida |
| E2 | y=x + x y=x + 4 | y=x + 4 | Inducida |
| E3 | y=x + 4 | y=x + 4 | Inducida |
| E4 | y=x + 4 y=x + x | y=x + 4 | Inducida |
| E5 | y=x + 4 | y=x + 4 | Inducida |
| E6 | y=x + 4 | y=x + 4 | Inducida |
En este trabajo se interpretan las estructuras identificadas por los estudiantes durante los casos particulares y el caso general. Cada estudiante puede evidenciar diferentes estructuras a lo largo de entrevista. En el caso que haya más de una estructura, las recogemos según su orden cronológico de aparición. Se expresan las estructuras identificadas mediante simbolismo algebraico, aunque ellos no emplearan ese sistema de representación, como se verá en los ejemplos posteriores.
Forma directa
En la Tabla 3 se presentan los resultados relativos a las respuestas al problema que involucra la forma directa de la función donde el dato conocido es el valor de la variable independiente (dada la edad de Iron Man se les pregunta por la edad del Capitán América). Nombraremos mediante una E y un número (del 1 al 6) a los distintos estudiantes para mantener su anonimato.
En las respuestas a las preguntas que involucran casos particulares y caso general se observan tres tipos diferentes de estructuras: y=x+4, y=4x, e y=x+x. Cada estudiante evidenció una o dos estructuras diferentes en su trabajo. Los seis estudiantes evidenciaron la estructura y=x+4 en el trabajo con preguntas relativas a casos particulares. Dos de ellos −E2 y E4− identificaron la relación y=x+x y ofrecieron la misma variedad en el tipo de estructuras; y una relación dada por una operación aditiva (y=x+x), para los casos particulares.
Con respecto al caso general, los seis estudiantes evidenciaron la estructura y=x+4. E1, adicionalmente, muestra la estructura y=4x. Este estudiante expresó inicialmente que hay que “multiplicar por 4” para obtener la edad del superhéroe mayor. Todos los estudiantes expresaron verbalmente la generalización.
Tres estudiantes −E2, E3 y E4− generalizaron a partir de la estructura y=x+4 al expresar: “hay que sumar más 4”. Sin embargo, los estudiantes E1, E5 y E6 evidenciaron esa estructura empleando valores concretos para referirse a la edad del superhéroe.
E l generalizó tanto espontánea como inducidamente. Desde el inicio de la tarea (trabajo con valores concretos), identificó la estructura, tratándose por tanto de una generalización espontánea. Al continuar con la entrevista generalizó inducidamente cuestiones relativas al caso general (generalización inducida). En el siguiente fragmento, la generalización espontánea de E1, observada durante preguntas sobre casos particulares.
I (Entrevistador): Cuando Iron Man cumplió 5 años el Capitán América cumplió 9. Cuando Iron Man cumplió 7 años, el Capitán América cumplió 11. Y cuando Iron Man cumplió 3 años, el Capitán América cumplió 7 años. ¿Puedes decirme alguna relación entre esos números? E1 (Estudiante1): El Capitán América siempre le gana por 4 años más. Los demás estudiantes (E2, E3, E4, E5 y E6) generalizaron únicamente de manera inducida, cuando se les preguntó por el caso general. A continuación, ejemplo de generalización inducida. I: ¿Cómo le explicarías a un amigo qué ha de hacer para conocer la edad del Capitán América? E5: Iron Man tiene 4 años menos que el Capitán América y el Capitán América tiene 4 años más que Iron Man. Se llevan 4 años.
Forma inversa
En la Tabla 4 se presentan los resultados relativos a la forma inversa de la función donde el dato conocido es el valor de la variable dependiente (dada la edad del Capitán América se les pregunta por la edad de Iron Man).
Tabla 4: Estructuras identificadas en la forma inversa de la función
| Estructura | |||
|---|---|---|---|
| Estudiante | Casos particulares | Caso general | Tipo de generalización |
| E1 | x = y - 4 | NR | NA |
| E2 | x = 2y | NP | NA |
| E3 | x= y - 4 | x= y - 4 | Inducida |
| E4 | NP | NP | NA |
| E5 | x = y - 4 | x = y - 4 | Espontánea e inducida |
| E6 | x = y - 4 | x = y - 4 | Inducida |
Nota: NR = no responde; NP = no se le pregunta; NA = no aplica.
En total evidenciamos dos tipos diferentes de estructuras, incluidas tanto las dadas en los casos particulares como en el caso general x=y-4 y x=2y. Cada estudiante evidenció una única estructura a lo largo de la entrevista. Salvo E2 y E4, todos señalaron la regularidad x=y-4 en algún momento de su trabajo, tanto en los casos particulares como en el general. Por su parte, E2 identificó la estructura x= 2y y a E4 no se le preguntó por la forma inversa por haberse encontrado cansado y disperso en ese momento de la entrevista.
Todos los estudiantes expresaron la generalización verbalmente. Para la forma inversa de la función también se distingue entre generalización inducida y espontánea. El estudiante E1 no respondió en esa ocasión a la pregunta del caso general. A E2 y E4 no se les preguntó por el caso general, ya que se encontraban distraídos en esta última parte de la entrevista. Las generalizaciones de E3 y E6 fueron inducidas. Por ejemplo, E6 expresó “antes sumaba y ahora resto, yo siempre estoy restando 4”. Se muestra un fragmento de entrevista con E3 donde evidencia este tipo de generalización:
I: ¿Cómo explicarías cómo calcular la edad del Capitán América conociendo la de Iron Man? E3: Cuando nació Iron Man tenía el Capitán América 4 años y después vas sumando los años. I: ¿Qué has hecho tú? E3: Una resta, aquí: 9-4, 8-4, 352-4.
Por otro lado, E5 generalizó tanto de forma espontánea como inducida. Al preguntar por los casos particulares, E5 expresó: “antes sumaba 4; ahora resto 4” (generalización espontánea). Ante la pregunta sobre el caso general, E5 contestó: “Siempre resto 4” (generalización inducida).
Conclusiones
A la luz de los resultados, reconocemos que los niños de 7-8 años evidenciaron capacidades para identificar estructuras en tareas de generalización que involucran una función lineal. Esta capacidad se pone de manifiesto para las formas directa e inversa de la función. Dado el tamaño de la muestra, se destaca que la intención no es generalizar, pero sí tenemos una prueba de existencia con unos niños que no tienen capacidades por encima ni por debajo de la media en España.
En cuanto a la consecución de los objetivos de investigación, se han identificado las diferentes estructuras evidenciadas por los estudiantes de educación primaria en relación con la realización de la tarea de generalización. Observando el tipo de generalización que cada uno expresa en el contexto que involucra la función y=x+4, se han extraído diferencias entre las estructuras identificadas por los estudiantes en la forma directa e inversa de la función.
Durante el estudio de la forma directa se obtiene una mayor variedad de estructuras −y=x+4, y=x+x e y=4x− frente a dos tipos de estructuras diferentes evidenciadas durante el estudio de la forma inversa (x=y-4 y x=2y). Si durante el estudio de la forma inversa tenemos en cuenta a los estudiantes E2 y E4 (a los que no se les preguntó por la generalización en la forma inversa), se concluye que todos los estudiantes identificaron la estructura adecuada para los casos particulares y para el caso general, excepto E2.
En los hallazgos obtenidos para la forma directa se observa que hay más estructuras erróneas que en el caso de la forma inversa. Las preguntas correspondientes a la forma inversa se hicieron al final de la entrevista, lo cual pudo influir en la motivación o cansancio de los niños. Este aspecto no es abordado en los resultados de otros trabajos de nuestros antecedentes. Sin embargo, en los resultados obtenidos en Pinto y Cañadas (2017a) encontramos más estructuras erróneas al trabajar con la forma inversa de la función que con la forma directa, al contrario de lo que en encontramos en este estudio.
La variedad de las estructuras identificadas durante el estudio de la forma directa de la función d certeza sobre la búsqueda de regularidades por parte del estudiantado. En este estudio se ha considerado que la forma directa involucra una adición y la forma inversa implica una sustracción. Se hizo así porque consideramos que la primera iba a resultar más accesible para los estudiantes. Sin embargo, hay más variedad de estructuras adecuadas proporcionadas durante el trabajo de la forma inversa (en total, atendiendo tanto a los casos particulares como al caso general) que en el trabajo con la forma directa.
Las estructuras demostradas en el trabajo con las formas directa e inversa, durante el primer momento de la entrevista (casos particulares), se han mantenido y generalizado para todos los estudiantes. Además, se hace referencia a la estabilidad de la estructura evidenciada por estos en casos particulares y más tarde en el caso general para cada una de las formas directa e inversa. Aunque la estabilidad es menor en la forma directa que en la inversa (teniendo en cuenta al estudiante que no contesta y a los dos a los que no se les pregunta), se evidencia coherencia en las estructuras identificadas tanto en los casos particulares como en el general por la mayor parte de los estudiantes; con excepción de E1 que no lo cumple, pues evidencia junto con la estructura adecuada otra que es errónea: y=4x. Esto concuerda con lo observado en Torres, Cañadas y Moreno (2018), quienes entrevistaron a seis estudiantes de entre 7 y 8 años e identificaron la estructura correcta de la función que implicaron (y=x+3), al menos en una ocasión, a lo largo de la entrevista, durante el estudio de la forma directa de la función.
Al igual que ocurre en el trabajo de Warren, Miller y Cooper (2013), cuando los estudiantes toman conciencia de la estructura, las conversaciones con ellos tienden a disminuir y a dar respuestas con una clara validación de la regularidad encontrada entre las variables. Esto informa sobre la consciencia de la estructura establecida por estos estudiantes de primaria.
En cuanto al tipo de estructuras erróneas identificadas, se destaca la estructura y =x+x. En este trabajo es comprobada por dos estudiantes en el trabajo con casos particulares de la forma directa de la función; Torres, Cañadas y Moreno (2018) la encuentran en tres de los seis estudiantes entrevistados que trabajaron con un problema que involucraba la función y=x+3. Con la forma inversa de la función se halla la estructura multiplicativa x=2y, equivalente a la aditiva x= y+y, en una ocasión, durante el trabajo con los casos particulares. Esta estructura, que verbalmente se corresponde con “sumar un número consigo mismo”, aparece en las dos formas de la función como estructura errónea. Este hallazgo puede deberse a que, con algún caso particular, el resultado coincidía con el doble del valor de la variable independiente o porque están familiarizados con la suma de un número consigo mismo. También se destaca la estructura y=4x, presente en la respuesta de un estudiante a la pregunta para el caso general en la forma directa. Su respuesta fue la siguiente: “hay que multiplicar por 4” para obtener la edad del superhéroe mayor. Inferimos aquí una dificultad al confundir una estructura aditiva con otra multiplicativa.
La generalización más frecuente ha sido la inducida con la forma directa de la función (cinco de seis estudiantes). Solo E1 generaliza en las formas espontánea e inducida. Durante el estudio de la forma inversa, dos de los tres estudiantes que respondieron evidenciaron generalización inducida (generalizaron al preguntarles por el caso general). El estudiante E5 presenta generalización espontánea e inducida para la forma inversa. La generalización inducida es la generalización esperada, ya que en realidad no necesitaban generalizar para responder a las cuestiones sobre casos particulares. Lo destacable es que algunos estudiantes de segundo curso generalizaran y fueran conscientes de la utilidad de la generalización para hallar la respuesta a las preguntas sobre casos particulares.
Finalmente se concluye destacando el interés de promover el trabajo con las formas directa e inversa de una función. Los estudiantes de estas edades (7-8 años) las han abordado a través de estructuras que les permiten dar sentido a problemas en contextos cercanos para ellos.
La mayor parte de las estructuras identificadas fueron adecuadas al problema y esto anima al trabajo con ambas formas de las funciones lineales en educación primaria. Destacamos la necesidad de realizar más investigaciones en este sentido, porque permitirían aproximarse, de una forma más profunda, a las relaciones entre dos variables en el ámbito del pensamiento funcional.
Financiamiento
Este trabajo se ha realizado en el proyecto con referencia EDU2016-75771-P, financiado por la Agencia Estatal de Investigación (AEI) de España y el Fondo Europeo de Desarrollo Regional (FEDER).
Declaración de la contribución de los autores
Todo el equipo de autoría afirmamos que se leyó y aprobó la versión final de este artículo.
El porcentaje total de contribución para la conceptualización, preparación y corrección de este artículo fue el siguiente: M. D. T. 35 %, M. C. C. 30 %, A. M. 20% y P. G. 15%.