Introducción
Desde la investigación en educación matemática, la resolución de problemas es probablemente el campo más estudiado, que además ha evolucionado de acuerdo con las demandas sociales. Los currículos escolares invitan a resolver problemas en diversas circunstancias sociales, laborales e interdisciplinarias (English & Gaingsburg, 2016). Esta situación conlleva a que la resolución de problemas se presente desde dos perspectivas: como un medio para desarrollar otras habilidades o como una habilidad o fin en sí misma (Stacey, 2005; Stanic & Kilpatrick, 1989).
Independiente del punto de vista, diversos autores han consensuado que resolver problemas implica realizar actividades de alto nivel cognitivo, dado que se caracteriza por la búsqueda de estrategias de resolución y el fomento del desarrollo de pensamiento matemático (Lesh & Zawojewski, 2007; Lester & Kehle, 2003). Los estudiantes exploran, conjeturan, experimentan y evalúan, por lo que estas estrategias tienden a ser personales; se les solicita responsabilidad matemática sustancial, se les estimula para generar preguntas por sí mismos y para prever posibles generalizaciones de los resultados obtenidos (Artigue & Blomhøj, 2013).
Por lo tanto, el tratamiento de la resolución de problemas desde la didáctica de las matemáticas emerge, por un lado, de la necesidad de estudiar su funcionalidad como recurso para el aprendizaje de los objetos de conocimiento del área; por otro, en relación con el desarrollo de destrezas y capacidades: el análisis, la síntesis, la extracción de información, la confrontación de ideas, la argumentación, la reflexión y la comunicación de resultados. Esto lo convierte en una potente herramienta para conocer cómo el alumno aprende, comprende y organiza su conocimiento.
La metacognición se define como “el conocimiento y control que uno tiene sobre su pensamiento y sus actividades de aprendizaje” (Swanson, 1990, p. 306). El conocimiento metacognitivo se refiere desde el aprendizaje de las matemáticas a los procesos y técnicas matemáticas que realizan los estudiantes, así como a sus ideas sobre la matemática (Özsoy & Ataman, 2009).
La metacognición puede considerarse desde dos epígrafes principales: el conocimiento metacognitivo y el control metacognitivo (Flavell, 1999; Otani & Widner, 2005). Conocer ambos puede ser de utilidad al docente para diseñar una instrucción matemática eficaz. Loh & Lee (2019) consideran este control separado en dos: el monitoreo y la regulación. Por ello, la resolución de problemas se convierte en una gran fuente de información en este sentido. Al situar a un estudiante ante un problema ha de conocer un abanico de estrategias y elegir una de ellas, siempre teniendo en cuenta su autoconocimiento, respecto a sus capacidades. En este sentido, no se debe olvidar la importancia de las emociones en la consecución de la tarea matemática.
Este trabajo se centra en el análisis de la metacognición desde un aspecto muy concreto del proceso de resolución de problemas, la representación; al centrar en lo posible, el análisis de las tareas de los estudiantes en las dimensiones que se tienen en cuenta al abordar la resolución de problemas desde la perspectiva metacognitiva, que son “planificar, monitorizar y evaluar” (Santos y Lozada, 2013, p. 43). Cada una de estas dimensiones y su estudio cobran sentido a través de la propia reflexión del aprendizaje durante la ejecución de la tarea, situación sin la cual no podría hablarse de metacognición; es necesario, por tanto, que el estudiante pueda conocer, controlar y autorregular su propio funcionamiento intelectual.
Para ello planteamos esta investigación que utiliza problemas guiados “de carácter numérico, algebraico y geométrico” (Contreras y Del Pino, 2007, p. 27), con estudiantes del primer y tercer curso de Educación Secundaria Obligatoria (ESO) en España, planteando diferentes grados de dificultad en la tarea. El objetivo es analizar el uso de diferentes registros de representación en la resolución de los problemas, para conocer si aporta información adicional sobre los procesos de razonamiento seguidos por los alumnos en pro de estudiar con mayor precisión las diferencias en las estrategias metacognitivas utilizadas por los mismos durante la resolución. Para llevar a cabo este análisis, desarrollaremos tres objetivos específicos: caracterizar la identificación de la situación problemática a partir de la comprensión del enunciado; analizar las representaciones utilizadas en cada uno de los tipos de problemas y describir las estrategias metacognitivas utilizados por los estudiantes durante la resolución del problema.
Marco teórico
Metacognición y resolución de problemas
La inclusión de la resolución de problemas en los currículos escolares no es algo novedoso en la asignatura de matemáticas, pues se contempla desde civilizaciones antiguas como la griega o la romana, en donde formaba parte de la materia de estudio (Stanic & Kilpatrick, 1989).
Los problemas comprenden a todas aquellas situaciones para cuya resolución es necesario poner en funcionamiento la reflexión, la búsqueda de información, el razonamiento y el uso de estrategias (Gaulin, 2001), que a modo de piezas de un engranaje hagan girar el mecanismo de forma que nos conduzca a la resolución de este, eso sí, de una manera no inmediata pero sí meditada.
Bajo esta perspectiva la resolución de problemas es una metodología de enseñanza, donde confluyen y destacan cuatro dimensiones (Pifarré y Sanuy, 2001) que condicionan su utilización como herramienta de enseñanza-aprendizaje:
a) La importancia del conocimiento declarativo sobre el contenido específico del problema; b) el repertorio de estrategias generales y específicas que es capaz de poner en marcha el sujeto para resolver el problema concreto; c) el papel de las estrategias metacognitivas; y d) la influencia de los componentes individuales y afectivos de la persona que resuelve el problema […] destacando las actitudes, las emociones y las creencias sobre los problemas y su resolución (p. 297).
Desde este último punto, queremos partir con una deliberación por el carácter negativo que lleva implícita la palabra problema, que puede llegar a traducirse y convertirse en condicionante que juega en contra de la actividad desarrollada por los estudiantes; para evitarlo, hay autores que sustituyen el término por “tarea” e incluso dentro de estas, las clasifican entre “tareas de práctica y tareas problemáticas” (Rodríguez, 2005, p. 33). En esta investigación partiremos del término problema, con el significado que le dan Vila & Callejo (2004, p. 31), “designar una situación, planteada con finalidad educativa, que propone una cuestión matemática cuyo medio de solución no es inmediatamente accesible”, con el propósito de minimizar creencias, actitudes y emociones de carácter negativo hacia los mismos.
Variadas son las funcionalidades que pueden atribuirse a la resolución de problemas, lo que permite orientarla como estrategia de aprendizaje desde tres enfoques distintos: “enseñanza para la resolución de problemas; enseñanza sobre la resolución de problemas y enseñanza vía la resolución de problemas” (Blanco & Cárdenas, 2013, p. 138); como vemos, ya desde la denominación de cada enfoque las diferencias radican en el uso, pues la primera se centra en la utilización de los problemas como elementos que permiten poner en práctica contenidos y conocimientos ya adquiridos; la segunda parte de la construcción y búsqueda de técnicas y estrategias de resolución, de modo que la formación se encuentra orientada hacia saber cómo enfrentarse a un problema; y la tercera lo concibe como estrategia de aprendizaje a partir de la que el estudiante construye conocimiento.
En cualquiera de los casos estaríamos implicando estrategias metacognitivas, en el sentido que tanto planificar como el proceso de búsqueda, resolución y comprobación implicado en el proceso de resolución del problema, demanda que el estudiante reflexione durante el proceso, al optar por “un procedimiento u otro para seleccionar los datos, elegir una u otra operación, utilizar un algoritmo o no y al término, una evaluación del resultado para saber si responde como solución del problema” (Arteaga & Macías, 2016, p. 2).
De acuerdo con la National Council of Teachers of Mathematics, NCTM (2000), los niños y niñas deben tener oportunidades para formular problemas dentro de una variedad de situaciones, realizar conjeturas, generalizar y extender tales problemas y recomienda que los estudiantes en todos los niveles “expliquen su razonamiento, validen sus afirmaciones y discutan y cuestionen su propio pensamiento y el pensamiento de otros” (Lampert, 1990, p. 33).
El desarrollo de un proceso de enseñanza en donde el estudiante ocupe el centro del escenario de aprendizaje, al generar ideas de manera autónoma desde la propia práctica, a partir de conocimientos previos que pueden verse modificados y adaptados al ante la necesidad de salvar obstáculos frente a las nuevas situaciones con las que se encuentra, desarrollar su tarea de forma consciente y razonada, estaría acorde con los principios recogidos por el NCTM. Esta situación nos permitirá hablar más aún de sus capacidades para reflexionar y describir (Schoenfeld, 1987) sobre la ejecución de la tarea, expresando cómo y por qué se realiza de una u otra forma, y qué procesos pone en práctica el estudiante durante y después de su realización.
Para el docente será importante conocer qué variables se ponen en práctica en la resolución de problemas matemáticos, en relación a las estrategias metacognitivas quizá aún más que las cognitivas. Por ello se deben elegir y crear problemas que faciliten experimentar, descubrir, conjeturar y comprobar las conjeturas (Leikin & Grossman, 2013), promover el pensamiento divergente, la reflexión y la persistencia.
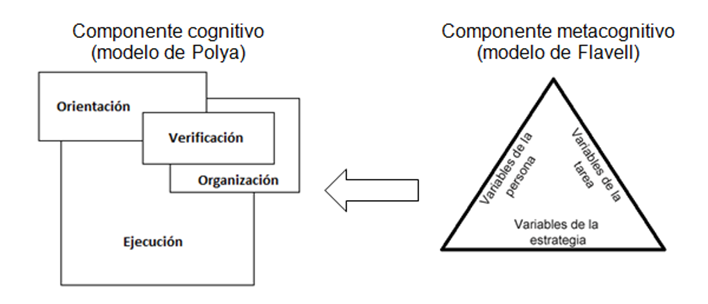
El modelo definido por Lester (1983) para la resolución de problemas matemáticos (figura 1), donde se relacionan componentes cognitivos establecidos en el modelo de Polya y los metacognitivos del modelo de Flavell (1999), es el punto de partida en este sentido.
Este marco de análisis facilita el estudio y evaluación de las acciones de autorregulación que llevan a cabo los estudiantes a la hora de resolver problemas, se parte de los procedimientos de comprensión del problema (orientación), la elección de una estrategia para abordarlo (organización), la puesta en funcionamiento de dicho plan (ejecución) y la posterior evaluación de la idoneidad de la estrategia seleccionada y el resultado obtenido (verificación). Esta perspectiva debe enfocarse desde el propio conocimiento del estudiante como individuo cognoscente, el conocimiento de la naturaleza de las tareas cognitivas, así como desde las propias estrategias (Rigo, Paez & Gómez, 2010).
En relación con la resolución de problemas, la regulación metacognitiva favorece tanto la comprensión como la propia búsqueda de caminos para solucionarlos de manera efectiva y reflexionada, pues investigaciones previas revelan que las estrategias metacognitivas pueden entrenarse y aportan valor añadido a los procesos de resolución de problemas (Desoete, 2007).
En este sentido, Domenech (2004) puso de manifiesto cómo la resolución de problemas contribuye a desarrollar procesos metacognitivos que favorecen la autonomía del estudiante en el aprendizaje de las matemáticas, partimos de la idea de que el estudio conjunto de la capacidad intelectual y la capacidad metacognitiva de los estudiantes, “si conocemos qué aspectos están incluidos en la resolución, qué procesos subyacen a la respuesta exitosa y qué características muestran las personas que resuelven correctamente, tendremos las pautas necesarias para educar en la resolución de problemas” (p. 63).
Por su parte, Silva (2004) comprende la regulación metacognitiva en la resolución de problemas como un proceso que consta de tres fases: la planeación o planificación, el control o supervisión y la evaluación (PCE). De este modo, piensa que es posible la mejora en la resolución de los problemas matemáticos, ya que permite conocer el proceso de comprensión y resolución, así como los factores que influyen en ello.
La planeación consiste en prever qué estrategias, técnicas o recursos hay que conjugar para poder abordar la tarea problemática los más efectivamente posible; el control permite comprobar si las acciones que se están llevando a cabo se corresponden con lo planificado, al detectar dificultades, obstáculos y las causas de los mismos para encontrar alternativas en caso de que sea necesario; la evaluación, por su parte, se centra en estudiar la idoneidad y efectividad del plan establecido, los procesos de realización y comprobación de los resultados obtenidos (Elosua, 1993).
En cada uno de estos tres momentos principales (PCE), los sistemas de representación van a ser indicadores del grado de compresión del problema (Kapa, 2007), las representaciones utilizadas en el proceso de resolución pueden ser más completas y, por tanto, de mayor utilidad en el establecimiento de una secuencia o pasos en la resolución.
El trabajo con la resolución de problemas debe combinar en la medida de lo posible las dos teorías clave que explican cómo funciona el pensamiento en este proceso: la teoría del pensamiento asociacionista y la teoría de la Gestalt (Peñalva, 2010). La primera, se basa en pruebas de ensayo y error, mientras que la segunda responde a las relaciones establecidas entre los distintos aspectos del problema como una estructura única.
Sternberg (1988) demuestra que los programas metacognitivos que contemplan mayores variables de planeación, control y evaluación logran mayores niveles de efectividad, y es ahí donde la utilización de la representación cobra importancia dentro de nuestro estudio.
Los registros de representación en la resolución de problemas
El primer encuentro entre el estudiante y la actividad matemática que va a realizar, le sitúa ante un escenario, donde junto a la componente conceptual y simbólica hace aparición la representativa: construcciones y figuras geométricas, dibujos e imágenes icónicas que evocan situaciones, esquemas u organizadores visuales, gráficas cartesianas, enunciados escritos en su lengua materna, etc., son solo una pequeña muestra de los recursos que disponemos en la construcción y enseñanza del conocimiento matemático.
El vínculo existente entre la utilización de un determinado sistema de representación ya sea discursivo (lengua materna, álgebra, numérico, etc.) o no discursivo (dibujo icónico, gráfica, material manipulativo, etc.) y los contenidos matemáticos que representan, se sustenta en los procesos cognitivos que se ponen en funcionamiento. Esta relación es un potente indicativo del tipo de comprensión y formación de conocimiento que tiene lugar en los estudiantes en la enseñanza-aprendizaje de estos contenidos. Investigaciones específicas que relacionan el dibujo situacional con el dibujo matemático como la llevada a cabo por Rellensmann, Schukajlow y Leopold (2017), señalan que “la precisión de los dibujos matemáticos está fuertemente relacionada con el rendimiento de los estudiantes” (p. 53).
Investigaciones similares, abordadas tanto desde el campo de la didáctica de las matemáticas como desde la propia psicología, parten de una misma premisa: la comprensión e interiorización que los alumnos desarrollan acerca de un determinado objeto matemático, se ve fortalecida y consolidada cuantas más conexiones se establezcan entre los múltiples registros de representación que permiten trabajar con dicho objeto (Duval, 2016).
Al atender los trabajos presentes en la literatura previa, y centrándonos en el trabajo de Duval (1993), podemos agrupar los sistemas de representación en siete principalmente, como se observa en la Tabla 1:
Tabla 1 Registros de representación
| Tipo de registro | Descripción |
|---|---|
| Lengua natural (RLN) | Se corresponde con la lengua materna. Facilita enunciar propiedades, definiciones, teoremas, etc. |
| Figural-icónico (RFI) | Engloba croquis, trazos, dibujos sencillos, material manipulativo, etc., que facilitan visualizar los conceptos matemáticos a trabajar sin hacer referencia explícita de sus características y propiedades. |
| Numérico (RN) | Se trata del sistema de numeración decimal el cuál permite abordar el estudio de ciertas características y propiedades de los objetos matemáticos. Del mismo modo permite realizar cambios de ordenes de unidades, composiciones y descomposiciones numéricas, así como realizar operaciones de cálculo. |
| Tabular (RT) | Facilita el estudio de los objetos matemáticos a los que representa mediante la organización de los datos en filas y columnas, lo que permite establecer relaciones y realizar comparaciones. |
| Algebraico (RA) | Registro de representación matemático por excelencia a través del cual se pueden expresar generalizaciones y propiedades, así como realizar modelizaciones. |
| Geométrico (RGe) | Formado por elementos lineales (puntos, líneas, segmentos, etc.) Figuras planas (polígonos regulares e irregulares) y cuerpos en el espacio. Facilita operaciones de reconfiguración, descomposición y composición para la comprensión de las nociones puestas en juego. |
| Gráfico (RGr) | Engloba al plano cartesiano y todos sus elementos, los cuales permiten analizar y estudiar el comportamiento de funciones, relación entre variables, así como el estudio de tratamientos propios de su registro entre ellas las traslaciones, reflexiones, simetrías, contracciones, dilataciones, etc. |
Nota: Elaboración propia a partir de Duval (1993)
Cada uno de los registros de representación hace referencia a unas características concretas del objeto al que está representando, de modo que, si con todos ellos se hace referencia a un mismo objeto de conocimiento, cada uno manifestará unas determinadas propiedades. La coordinación y utilización de múltiples registros de representación nos proporciona, por un lado, una configuración de los conceptos en toda su extensión y profundidad, y por otro, una visión de los procesos de razonamiento y comprensión que tiene el estudiante, porque las representaciones que utilice son indicativos de la percepción que ha generado del concepto en cuestión.
Este hecho se pone especialmente en manifiesto cuando un alumno se enfrenta a un problema, ya que, tras la lectura del enunciado, dado en el lenguaje de la lengua natural, va a ser necesario, para su resolución, realizar una conversión hacia otro registro, ya sea numérico, figural, geométrico, etc., incluso trabajar de forma simultánea con más de un registro, lo que pone de manifiesto el tipo de comprensión que ha realizado sobre el propio problema (Duval, 1993, 2004).
Otro aspecto por destacar cuando vinculamos la utilización de múltiples registros de representación con la resolución de una situación problemática es el denominado cambio de anclaje. Según Duval (2004), se trata de un proceso de gran trascendencia e importancia a la hora de resolver problemas, especialmente de tipo geométrico, pues el cambio de anclaje consiste en el establecimiento de un vínculo entre el contenido del problema presentado de manera discursiva y la representación visual que se genera a partir de él (cambio de anclaje de lo discursivo a lo visual) o las afirmaciones matemáticas que expresamos discursivamente a partir de la representación visual que aparece de partida en el problema (cambio de anclaje de lo visual a lo discursivo).
Todo lo expuesto, nos conduce de manera necesaria al estudio del tipo de representaciones y coordinación que establecen entre ellos los estudiantes a la hora de enfrentarse a la resolución de un problema, pues es una importante fuente de información con respecto a los procesos metacognitivos desarrollados por los estudiantes.
Metodología
La experiencia de análisis está basada en el marco teórico previo y se desarrolla con una muestra no aleatorizada de 99 estudiantes de secundaria, de un colegio concertado del centro de Madrid. De ellos un 41.41 % son de primero (12 años) y un 58.59 % de tercero (14 años).
El instrumento para la recogida de los datos implica problemas verbales con contenidos centrados en el manejo numérico y geométrico. El nivel de dificultad de este, en todos los problemas seleccionados se considera inferior con el que debería tener el estudiante, de acuerdo con el curso en que se encuentra escolarizado, de esta forma su dificultad no será un distractor para la observación de las estrategias metacognitivas y la representación.
La resolución se organiza de acuerdo con siete cuestiones (anexo 1). El espacio destinado para esta es limitado, en el documento que se entrega a los estudiantes, factor que circunscribimos dentro de los incluidos en la tipología de la tarea (Lester, 1983) como parte de la organización de los elementos dados (Puente, 1993). En cada curso se utilizaron dos tipologías de problemas de acuerdo con el contenido, uno numérico y otro geométrico, obtenidos y adaptados de las pruebas de diagnóstico TIMSS y Evaluaciones de diagnóstico.
La Tabla 2 recoge, a modo de ejemplo, los problemas de carácter numérico (tipo A) y de carácter geométrico (tipo B) para ambos cursos:
Tabla 2 Problemas utilizados
Nota: Fuente propia de la investigación.
Basándonos en la teoría previa, se establecen categorías de análisis en cada una de las dimensiones. Por ejemplo, la relación existente entre la representación efectuada por el alumno y el enunciado del problema propuesto nos permitirá clasificar el nivel de comprensión que dicho alumno tiene del mismo, a través de la representación utilizada y las unidades significantes que componen cada uno de ellos, al entender por unidades significantes de una representación, los elementos y propiedades matemáticas que lo caracterizan en relación con el contenido matemático que se aborda en el problema.
No evidencia comprensión (A): descriptivo, sin ningún tipo de conocimiento matemático asociado o estrategia vinculada.
Evidencia comprensión parcial (B): utiliza un registro o registros asociados a una estrategia, pero con ausencia de algún dato imprescindible o algún error.
Evidencia comprensión total (C): utiliza un registro o registros asociados a una estrategia de manera completa.
La selección de las codificaciones que conciernen a la fase de planeación, que hacen referencia al modo en cómo el alumno expresa lo que demanda el problema, nos permite determinar el grado de razonamiento y comprensión inicial de este. Si el estudiante plasma la pregunta tal cual aparece en el problema, habrá realizado una simple lectura de este; si opta por la expresión con sus propias palabras sin dar más detalles, estaremos ante una asimilación de la problemática, sin llegar a reflexionar sobre la manera de resolverlo, al igual que en el primer caso; mientras que, si se corresponde con la opción C, el estudiante habrá completado todo un proceso de razonamiento inicial.
La codificación completa que se utilizará para el análisis, sustentada en el marco teórico expuesto, se muestra en el anexo 1.
Resultados
La mayoría de los estudiantes reconocen la pregunta (Tabla 3), es ligeramente superior el porcentaje para el problema geométrico, en ambos cursos.
Tabla 3 Reconocimiento de la pregunta según el tipo de problema
| Curso | Reconoce la pregunta | |||
|---|---|---|---|---|
| No | Sí | |||
| 1ºESO | Tipo de problema | A | 22.0 % | 78.0 % |
| B | 2.4 % | 97.6 % | ||
| 3ºESO | Tipo de problema | A | 1.7 % | 98.3 % |
| B | 100.0 % | |||
Nota: Fuente propia de la investigación.
A la hora de reconocer el planteamiento de la pregunta (Tabla 4), se repite la pauta en ambos cursos; mientras que en A la mayoría la expresan tal cual está en el enunciado (65.9 % y 96.9 %, para cada uno de los cursos); en B, la expresan utilizando sus propias palabras, pero no parte de la estrategia (53.7 % y 79.3 %). Vemos como estas diferencias son más acentuadas entre los alumnos de tercer curso.
Tabla 4 Reconocimiento de la pregunta según el tipo de problema
| Curso | Modo de expresión | |||||
|---|---|---|---|---|---|---|
| No responde | La expresa tal cual está en el enunciado | La expresa utilizando sus propias palabras, pero no manifiesta parte de la estrategia | La expresa utilizando sus propias palabras manifestando parte de la estrategia | |||
| 1ºESO | Tipo de problema | A | 7.3 % | 65.9 % | 24.4 % | 2.4 % |
| B | 2.4 % | 41.5 % | 53.7% | 2.4 % | ||
| Total | 4.9 % | 53.7 % | 39.0 % | 2.4 % | ||
| 3ºESO | Tipo de problema | A | 1.7 % | 96.6 % | 1.7 % | |
| B | 19.0 % | 79.3 % | 1.7 % | |||
| Total | .9 % | 57.8 % | 39.7 % | 1.7 % | ||
Nota: Fuente propia de la investigación.
Respecto al registro de representación, cambia de un problema a otro, como podemos ver en la Figura 2.
En el problema numérico los estudiantes utilizan el registro icónico de manera preferente, sin embargo, esta diferencia es más amplia en el caso de tercer curso. Además, en el caso de tercer curso los alumnos utilizan el registro numérico como segunda opción, mientras que esto es distinto en primero que lo hacen con la lengua natural. En el caso del problema B, es el registro geométrico el que prevalece sobre los demás siendo el icónico el que ocupa la segunda opción; el rango en la diferencia es mayor en el caso de 3ºESO.
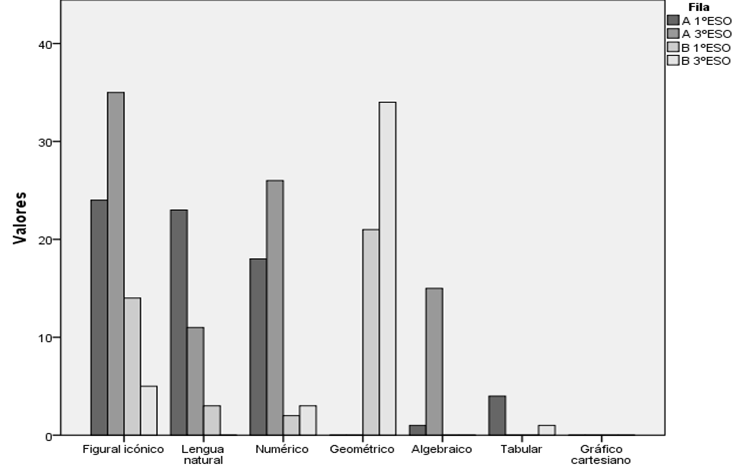
Figura 2 Registros de representación utilizados en la resolución. Fuente propia de la investigación.
Dado que cada estudiante puede elegir más de un tipo de representación en cada resolución, analizamos en la Tabla 5 si está asociado el número de registros con la tipología de problemas. Calculamos además el coeficiente de contingencia, al obtener un valor de .530 con un p-valor de .00 lo que indica una clara dependencia entre el número de registros y el tipo de problema a resolver.
Tabla 5 Número de registros por tipo de problema
| Número de tipos de representación empleados | Total | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | ||||||
| Tipo de problema | A | 0 | 28 | 36 | 19 | 83 | |||
| B | 1 | 73 | 5 | 0 | 79 | ||||
| Total | 1 | 101 | 41 | 19 | 162 | ||||
Nota: Fuente propia de la investigación.
La mayoría de los estudiantes (Tabla 6) al relacionar la representación con el enunciado no demuestran comprensión en el problema tipo B, al presentar los resultados sin conocimiento matemático asociado o estrategia vinculada; sin embargo, los resultados son mejores en el problema numérico. El coeficiente de contingencia .243 (p-v: .006) confirma la dependencia de esta relación con el tipo de problema.
Tabla 6 Relación de la representación con el enunciado
| Relación de la representación con el enunciado | Total | |||||||
|---|---|---|---|---|---|---|---|---|
| No valorable | No evidencia comprensión: descriptivo, sin ningún tipo de conocimiento matemático asociado o estrategia vinculada | Comprensión parcial: utiliza estrategia pero con ausencia de algún dato imprescindible o... | Evidencia comprensión total | |||||
| Tipo de problema | A | 16 | 35 | 35 | 13 | 99 | ||
| B | 21 | 33 | 17 | 28 | 99 | |||
| Total | 37 | 68 | 52 | 41 | 198 | |||
Nota: Fuente propia de la investigación.
En cuanto a las estrategias de control, siguen en su mayoría los pasos en la resolución, apenas encuentran atajos, ni encuentran obstáculos durante ella.
En ambos problemas, al referirnos a la evaluación, los estudiantes no utilizan un plan de resolución previsto (78.28 %), relacionan la respuesta con la pregunta (68.69 %), no justifican la respuesta (80.81 %) y no consideran que tenga dificultad (58.59 %). En todos los casos, el cálculo de los coeficientes de contingencia señala niveles de significación por encima de .05 lo que indica, que las estrategias de evaluación mencionadas son independientes del tipo de problemas.
Lo resuelven de forma correcta, un 40.54 % el problema A, y 55.29 % el B. Cabe mencionar que estos datos son distintos ya que dependen del curso en el que nos encontremos, mientras que en primer curso el número de estudiantes que llegan al resultado correcto de ambos problemas es similar, en tercero, hay claras diferencias, pues resuelven de manera correcta el tipo A un 25.71 % y el tipo B un 63.83 %.
Conclusiones
La resolución de problemas constituye una importante y potente herramienta dentro del proceso de enseñanza-aprendizaje de las matemáticas, pues nos permite no solo evaluar el nivel de adquisición y aplicación de conceptos y procesos por parte del alumno, sino estudiar y analizar las estrategias metacognitivas que cada estudiante pone en funcionamiento a la hora de enfrentarse a tareas problemáticas, como hemos podido verificar a través de la experiencia descrita.
A la hora de caracterizar la identificación de la situación problemática a partir de la comprensión del enunciado, los resultados muestran que en el problema numérico los estudiantes reconocen la pregunta y la expresan de manera similar a la propuesta, mientras que en el problema geométrico la expresan con sus palabras, sin mostrar parte de la estrategia.
El estudio de la comprensión de enunciados, de la relación que se establece entre los datos que constituyen el problema y la cuestión a resolver, así como de los procesos de razonamiento que el estudiante debe articular a modo de engranaje con capacidades y habilidades como son la síntesis, el análisis, la visualización, la argumentación, la fluidez, la audacia, la autonomía, etc., fundamentales en la resolución de este tipo de tareas; nos aporta una visión bastante completa sobre aquellos aspectos en los que es necesario incidir para subsanar carencias o necesidades que manifiesten los alumnos en este quehacer que tan útil es en la vida, pues facilita una comprensión más general, detallada y efectiva de todo lo que nos rodea, para así poder afrontar situaciones complejas de nuestro día a día con mayor garantías de éxito.
En relación al análisis de las representaciones utilizadas en cada uno de los tipos de problemas de acuerdo a las características del problema por medio de la comprensión de este, los resultados muestran cómo los alumnos no la evidencian al relacionar la representación con el enunciado del problema de tipo geométrico, al contrario de lo que ocurre con el numérico. Esto podríamos explicarlo desde la propia práctica docente, que tiende a enfocarse en el trabajo numérico, aritmético y algorítmico, en detrimento de la movilización y desarrollo de capacidades que verdaderamente capaciten a los alumnos en las herramientas que les conduzcan a resolver los problemas de menara comprensiva. Es importante que tengamos en cuenta cómo el profesor debe conocer la demanda cognitiva y las características estructurales de los problemas para ajustarlos a las características de los estudiantes (García, San José & Solaz-Portolés, 2015).
La utilización del registro icónico a la hora de representar el problema de tipo numérico guarda relación con la falta de vínculos que se establecen entre el registro numérico y otros registros de representación como puede ser el tabular o incluso gráfico, que permiten visualizar los datos de manera general. Hemos de destacar la diferencia en el nivel de las pruebas numéricas seleccionadas con respecto al curso donde se desarrollaron; la prueba de primero se correspondía con un nivel de primaria tres cursos previos al objeto de estudio, mientras que la de tercero se corresponde con un curso por debajo. Estas diferencias, sin embargo, no se vislumbran en las diferencias de resultado.
Además, toda actividad y proceso matemático, y la resolución de problemas en particular, lleva consigo la necesidad de cambiar y coordinar distintos registros de representación. La importancia que guardan tales conversiones y coordinaciones con la comprensión significativa de las nociones matemáticas que subyacen en los problemas planteados, convierte a estos procesos en una pieza clave del proceso de enseñanza en nuestra área de conocimiento, a la par que evita el establecimiento y creación de obstáculos en el proceso de aprendizaje de los objetos matemáticos. De aquí su pertinencia dentro de este estudio.
A la hora de describir las estrategias metacognitivas utilizados por los estudiantes durante la resolución del problema, podemos señalar que se presenta más fortaleza en la estrategia de planeación, al reconocer de manera correcta la pregunta del problema geométrico, que utilizar, en este caso de manera preferente, el registro geométrico. En la estrategia de control siguen de manera general los pasos para la resolución y consideran que no tienen obstáculos durante el proceso. En cuanto a la evaluación, relacionan la respuesta con la pregunta en su mayoría, pero no justifican la respuesta; esto contrasta al relacionarla con el enunciado, que señala una no comprensión del problema, fundamentalmente geométrico.
Así, desde el objetivo planteado en el análisis de los registros de representación en la resolución de los problemas, planteamos la necesidad de que el estudiante reciba una instrucción metacognitiva que le facilite el razonamiento matemático desde la formulación y respuesta de una serie de preguntas centradas en comprender el problema, construir las conexiones con el conocimiento previo, uso de estrategias adecuadas y reflexión sobre el proceso y la solución (Kramarski, Mevarech & Arami, 2002).
Por otro lado, consideramos que debe hacer énfasis en el trabajo de resolución de problemas contextualizado y coherente que se lleva a las aulas. La investigación centrada en el profesorado ha observado que es usual que los profesores no propongan problemas (Pelczer & Gamboa, 2008; Singer, Ellerton & Cai, 2013), lo que conlleva una cultura de resolver problemas que otros crean (Ellerton, 2013), lo que focaliza la atención en la resolución de problemas por sobre la habilidad que el problema desarrolla y la construcción de otros problemas (Crespo, 2003). En la práctica, los profesores deberían, a lo menos, reformular enunciados para adaptarlos a su contexto (Rowland, Huckstep & Thwaites, 2003)
Si como docentes, dedicamos un tiempo a elegir o formular problemas adecuados para la construcción y consolidación de los contenidos trabajados, apropiados al nivel y desarrollo cognitivo de nuestros estudiantes, vinculados con sus posibles inquietudes e intereses, lo que genera en ellos un gusto por la investigación y el descubrimiento, estaremos más cerca de conseguir hacer de los problemas no solo una herramienta que potencia el aprendizaje significativo de nociones matemáticas, sino también un recurso que dota a nuestros alumnos de una serie de capacidades y destrezas que les permita afrontar obstáculos que se encuentren en su día a día. “Enseñar conductas metacognitivas a los sujetos tiene incidencia positiva en su desempeño cognitivo” (Coleoni & Buteler, 2008, p. 372).
Anexo 1 disponible en pdf