El proceso social de culturización científica ha planteado la necesidad de implementar modificaciones educativas en matemática basándose en diseños mejor adaptados a prácticas escolares. La matemática educativa se ocupa del estudio sistemático de los efectos de tales modificaciones (Cantoral y Farfán, 2003). En Latinoamérica se han reportado debilidades en la calidad en la enseñanza de matemáticas y ciencias, tanto en los niveles iniciales (Valverde y Näslund-Hadley, 2010) como en el nivel superior (López Leiva, 2016; Morales-López, 2017). Esto plantea la necesidad de investigar en matemática educativa para mejorar la formación de profesionales en distintas áreas.
Uno de los aspectos que ha adquirido relevancia dentro de la investigación en matemática educativa es el relativo a las representaciones. El hecho de que el quehacer matemático sea una de naturaleza simbólica ha sido señalado como una de las razones por las que la semiótica haya adquirido notable interés en el campo de la educación matemática (Radford, 2006). La importancia de los distintos sistemas de representación de objetos matemáticos (numérico, algebraico, gráfico, simbólico) para el desarrollo y el aprendizaje de las matemáticas ha sido consensuada en distintos foros y medios de difusión de profesionales de las matemáticas y de su enseñanza. Numerosos estudios han abordado la cuestión representacional en matemática desde distintos enfoques (Duval, 2004; Font, 2001; Kaput, 1991; Lacués, 2014; Pimm, 1990; Socas, 2007).
La importancia de los distintos sistemas de representación de objetos matemáticos (numérico, algebraico, gráfico, etc.) para el desarrollo y el aprendizaje de las matemáticas ha sido consensuada en distintos foros y medios de difusión de profesionales de las matemáticas y de su enseñanza. El hecho de que el quehacer matemático sea de naturaleza simbólica ha sido señalado como una de las razones por las que la semiótica haya adquirido notable interés en el campo de la educación matemática (Radford, 2006).
A las representaciones realizadas a través de signos tales como figuras, fórmulas algebraicas, gráficos, etc., Duval (1998, 2004) las denomina representaciones semióticas.
Respecto de la pluralidad de formas de representar un mismo objeto matemático, Duval (1998, 2004, 2006) subraya dos hechos fundamentales: por una parte, que toda representación semiótica es parcialmente cognitiva respecto de lo que representa; por otra parte, la necesidad de que un sujeto aprendiz distinga un objeto matemático de su representación para su conceptualización. A partir de estos hechos, afirma que la comprensión de un objeto matemático requiere que el estudiantado sea capaz de coordinar representaciones de este mismo en, al menos, dos registros de representación.
Dos de los registros de representación semiótica usados en álgebra son el registro del lenguaje algebraico y el registro gráfico. Las coordinaciones aludidas por Duval (2004) implican la habilidad de transformar representaciones de un objeto, plasmadas en el registro algebraico, a sus correspondientes gráficas, y transformaciones en el sentido inverso, donde a partir de la representación gráfica se pueda llegar, por ejemplo, a una ecuación o inecuación (o sistema de ellas) que las describa en el lenguaje algebraico.
Coordinar representaciones de un objeto matemático no solo es una condición necesaria para su conceptualización, sino que es relevante como habilidad para la tarea de resolución de problemas. En muchas ocasiones, en el inicio de la tarea matemática de su trabajo, un físico o un ingeniero tiene como datos una serie de observaciones, tal vez representados como puntos de una gráfica a los cuales debe poder interpretar y manipular. Esto determina que la habilidad de convertir representaciones del registro gráfico al algebraico tenga importancia para el desarrollo de competencias necesarias para satisfacer el perfil profesional.
Esta necesidad debe ser atendida desde el comienzo de la formación de profesionales. En el primer curso en el que se imparten conocimientos algebraicos de las carreras de Ingeniería que se dictan en la Universidad Nacional de Mar del Plata, Argentina, uno de sus núcleos temáticos es el referente al conjunto de números complejos. Se caracteriza por su gran riqueza semiótica por cuanto, en el registro gráfico, los números complejos pueden representarse en forma de puntos o de vectores en el plano y, en el registro algebraico, pueden expresarse, entre otras, como pares ordenados, en forma binómica o en forma polar; dichos registros posteriormente serán utilizados por el alumnado en el estudio de espacios vectoriales, variedades lineales en R2 y curvas planas o regiones del plano complejo descriptas en coordenadas cartesianas y polares y análisis de funciones de variable compleja.
Durante el desarrollo de las clases prácticas correspondientes a dicho núcleo temático, el personal docente a cargo observó que sus estudiantes utilizaban las representaciones gráficas solo como ilustración final de una práctica matemática y no como fuente de datos para iniciar una tarea. Así, por ejemplo, al resolver determinadas actividades que requieren transformar un número complejo de su forma binómica a su forma polar, se reparó que muchos educandos las llevaban a cabo focalizando su atención solo en las ecuaciones implicadas, sin recurrir al soporte de una representación gráfica. En muchos casos cometían errores que, de haber contemplado la representación gráfica del número complejo abordado, se hubieran percatado de tal error. En diálogos habituales, desarrollados entre docentes y estudiantes durante las clases prácticas, se constató que realizaban esta tarea limitándose al registro algebraico, sin considerar el registro gráfico como apoyo en la resolución. Esta subvaloración en el uso del registro gráfico fue señalada en investigaciones (Artigue, 1995; Guzmán, 1998; Hitt, 2003; Varettoni y Elichiribehety, 2010) en relación con variados contenidos matemáticos y en distintos niveles educativos, como consecuencia de un descuido en el trabajo de abordaje didáctico con las representaciones gráficas. Esta situación condujo a una revisión de la labor didáctica sobre la interpretación de representaciones gráficas, por lo que se examinó el material estudiado en las lecciones con el alumnado. Así pudo constatarse esta subvaluación del registro gráfico tanto en la guía de trabajos prácticos como en la bibliografía sugerida para dicha unidad. Particularmente, en las tareas de integración de la mencionada guía, se presentaban al estudiantado numerosos ejercicios donde debía operar tomando como punto de partida la definición de regiones del plano complejo, descriptas como conjuntos definidos por comprensión en el registro algebraico, proponiéndoles representarlos en un registro gráfico; sin embargo, no figuraban actividades que requirieran la transformación en el sentido inverso. Tampoco figuraban actividades de caracterización de representaciones gráficas de números complejos en la bibliografía recomendada. Cabe destacar que la habilidad de describir o representar regiones o curvas del plano complejo mediante ecuaciones o inecuaciones en el registro algebraico es necesaria para poder abordar distintos tópicos posteriores, como el de análisis de funciones de variable compleja. Esta habilidad, llamada conversión por la teoría de registros semióticos, es postulada desde esta teoría como condición necesaria para la conceptualización de un objeto matemático (D’Amore, 2011).
A partir de los hechos expuestos, se concibió la idea de contemplar la habilidad de conversión de representaciones de conjuntos de números complejos, desde el registro gráfico al algebraico, como un saber a enseñar. Esta idea generó la inmediata pregunta: ¿cómo diseñar una secuencia didáctica que favorezca esta habilidad? Esta fue la pregunta que dio origen a una investigación desarrollada con estudiantes de una asignatura de álgebra inicial de las carreras de Ingeniería que se dictan en la Universidad Nacional de Mar del Plata.
Respecto de la enseñanza de números complejos, se pueden mencionar como antecedentes, entre otros, los siguientes trabajos:
- Pardo-Salcedo y Gómez-Alfonso (2005) y Buhlea y Gómez-Alfonso (2007) confirman en sus investigaciones la vinculación de las dificultades de estudiantes al abordar el tema números complejos con las que han enfrentado los matemáticos a lo largo de la historia; en el trabajo de Buhlea y Gómez-Alfonso (2007) también se considera la influencia del modelo de enseñanza.
- Martínez-Sierra y Antonio (2009) investigan y confirman la factibilidad de la construcción escolar de los números complejos a través de un proceso de convención matemática.
En relación con la enseñanza de números complejos vinculada con sus representaciones existen algunos antecedentes en distintos niveles educativos. Para la escuela secundaria, Monzón (2010) realiza una indagación sobre los libros didácticos brasileños de ese nivel y un relevamiento sobre investigaciones realizadas en Brasil sobre la enseñanza de números complejos y concluye que, para que estudiantes de este nivel logren un aprendizaje significativo, se tienen varias alternativas de enfoque que incluyen su presentación histórica, su interpretación geométrica y el uso de software de geometría dinámica. También focalizado en la escuela secundaria, el trabajo de Canal-Martínez (2012) propone algunas pautas para la enseñanza de los números complejos mediante una aproximación epistemológica y el uso de software. Por otra parte, en el nivel universitario, Flores-González y Montoya-Delgadillo (2016) investigan sobre el proceso de aprendizaje de la multiplicación de los números complejos, con el objetivo de enseñar este contenido privilegiando el registro gráfico a partir de la teoría de espacio de trabajo matemático (Gómez-Chacón, Kuzniak y Vivier, 2016). La forma de planteo gráfico-geométrico implica la necesaria capacidad por parte del alumnado de que las resoluciones geométricas, representadas en el registro gráfico, sean traducidas al registro algebraico.
Precisamente esa habilidad, pero aplicada a curvas y regiones del plano complejo, es la que se buscó investigar cómo favorecer. Para ello se diseñó un instrumento para evaluar la habilidad de conversión mencionada y se estudiaron los aspectos involucrados en esa tarea de conversión. A partir de las observaciones logradas, se diseñaron e implementaron actividades de enseñanza con el objetivo de favorecer dicha habilidad y se testeó, posteriormente, su efectividad y su incidencia en la capacidad de gestión de los números complejos en la resolución de problemas.
El diseño de tales actividades, ajustado a escasos recursos temporales y materiales, planteó desafíos. El objetivo de este artículo es describir la secuencia didáctica, las variables de conversión que regulan los niveles de complejidad de las actividades que la componen y los resultados obtenidos de su implementación.
Marco teórico
Dado que la investigación que dio lugar a este artículo se refiere a cuestiones representacionales se exponen, a continuación, algunos conceptos vinculados a representaciones, en particular los detallados por la teoría de registros de representación semiótica de Duval (1998, 2004).
Representar puede entenderse como colocar algo en lugar de otra cosa. Así lo señala Rico (2009, p. 6) al indicar que “representar es sustituir, dar presencia a un ausente y, por tanto, confirmar su ausencia”. En el ámbito de la matemática este autor señala:
Las representaciones matemáticas se han entendido desde entonces, en sentido amplio, como todas aquellas herramientas -signos o gráficos- que hacen presentes los conceptos y procedimientos matemáticos y con las cuales los sujetos particulares abordan e interactúan con el conocimiento matemático, es decir, registran y comunican su conocimiento sobre las matemáticas. Mediante el trabajo con las representaciones las personas asignan significados y comprenden las estructuras matemáticas, de ahí su interés didáctico (Radford, 1998). (Rico, 2009, p. 3)
En su teoría de registros de representación semiótica, Duval (1998, 2004) diferencia las representaciones mentales de las semióticas.
Representaciones mentales: “son las que permiten mirar el objeto en ausencia total de significante perceptible” (Duval, 2004, p. 36). Comprende el conjunto de imágenes y concepciones que un individuo puede tener sobre un objeto, sobre una situación y sobre lo que le está asociado.
Representaciones semióticas: aquellas producciones constituidas por el empleo de signos (enunciado en lenguaje natural, fórmula algebraica, gráfico, figura geométrica, etc.).
Duval (1998, 2004) subrayó la importancia de las operaciones cognitivas que tienen lugar en la manipulación de las representaciones semióticas para la comprensión de esta ciencia. Sostiene que las representaciones semióticas no son solamente los medios de exteriorización de representaciones mentales a los fines de la comunicación, sino que son esenciales para la actividad del pensamiento. Si bien es comúnmente aceptado que al comprender o conocer un objeto, un sujeto es capaz de representarlo con algún símbolo o grafismo, esta teoría focaliza la atención sobre la habilidad de interpretar y coordinar representaciones como condicionante para la comprensión del objeto representado. El autor de esta teoría lo expresa aseverando que no hay noesis (aprehensión conceptual de un objeto) sin semiosis (o aprensión o producción de una representación semiótica), con lo que afirma su inseparabilidad.
Sobre la construcción de conceptos matemáticos, Duval (1998, 2004) establece que, dado que cada representación es parcial con respecto a lo que representa, se debe considerar como absolutamente necesaria la coordinación de diferentes representaciones del objeto matemático para la formación del concepto.
Distingue tres tipos de actividades cognitivas ligadas a la semiosis: (a) la formación de una representación identificable como registro, (b) el tratamiento como la transformación de una representación en otra en el interior del registro donde fue creada, y (c) la conversión, que implica la transformación de una representación dada en un registro en otra representación en un registro diferente.
Particularmente, la conversión de las representaciones semióticas constituye la actividad cognitiva menos espontánea y más difícil de adquirir para la mayoría de estudiantes y, con frecuencia, la ausencia de coordinación entre los diferentes registros genera un obstáculo para los aprendizajes conceptuales. Para poder efectuar la conversión de la representación de un objeto, de un registro a otro diferente, el estudiantado debe poder distinguir los elementos fundamentales dentro de la representación que Duval (1998, 2004, 2006) denomina unidades significantes.
Las conversiones que no son triviales ni inmediatas porque los elementos involucrados, es decir, las unidades significantes, no están en correspondencia uno a uno, se denominan no congruentes. Este tipo de conversiones, como es el caso de las planteadas en este trabajo, requieren de especial atención en el proceso de enseñanza y aprendizaje, y deben ser abordadas intencionalmente, dado que, como afirma D’Amore (2011), la conversión, en los casos de no congruencia, no se construye espontáneamente.
La conversión entre dos representaciones semióticas planteadas en distintos registros no presenta el mismo nivel de dificultad al cambiar el sentido de esta misma. Así, en general, es más utilizada y más sencilla la conversión de fórmulas del registro algebraico al registro gráfico que la tarea de hallar, para una representación gráfica, la fórmula o ecuación que la representa en el registro algebraico. En el primer caso, la construcción de un gráfico requiere solo calcular algunas coordenadas y trazar una curva en el sistema cartesiano según una regla de correspondencia par ordenado-punto. En la conversión desde el registro gráfico al algebraico se requiere de la habilidad de visualización para distinguir cuáles son los rasgos característicos del objeto representado y cómo se relacionan para poder luego representarlo como ecuación o inecuación (Duval, 1998).
Para propiciar la conversión desde el registro gráfico al algebraico, Duval (1998) sugiere que se diseñen actividades en las que el alumnado pueda distinguir las unidades significantes en el registro de partida y sus concomitantes en el registro de llegada. Dichas actividades son llamadas tareas de variaciones comparativas. En ellas, la variable independiente es la variación del contenido visual del registro inicial con las siguientes características:
De un gráfico a otro solo se cambia una variable visual a la vez, y no dos o tres.
La conversión no se realiza sobre una presentación aislada de los casos particulares.
La conversión se transforma en un método para analizar lo que es matemáticamente significativo en el contenido de la representación dada.
En este estudio los objetos matemáticos trabajados son subconjuntos de números complejos que describen curvas o regiones sobre el plano complejo. Los registros de representación semiótica implicados son el registro algebraico y el registro gráfico.
En este trabajo se considera registro algebraico a aquel en el que se pueden formar las representaciones de conjuntos de números complejos con ecuaciones o inecuaciones en términos de los elementos asociados a formas de par ordenado, forma binómica, forma trigonométrica y forma polar. Un ejemplo de representaciones de conjuntos de números complejos en este registro es el siguiente: 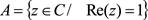 .
.
Se considera el registro gráfico que proporciona el plano de Argand-Gauss, es decir, el sistema cartesiano en el cual los números complejos son representados tanto como puntos del plano o como vectores. En dicho registro, los ejes cartesianos son presentados con las unidades marcadas para facilitar la lectura de las posiciones de las partes real e imaginaria de cada número complejo representado. Con idéntica consideración didáctica, se presentan líneas orientativas para agilizar la lectura de módulos y argumentos, como puede observarse en los gráficos presentes en la Figura 1.
Se entiende por secuencia didáctica a un conjunto de actividades ordenadas, estructuradas y articuladas para la consecución de unos objetivos de aprendizaje (Zaballa- Vidiella, 1995).
La habilidad que se pretende favorecer con la secuencia didáctica es la que está implicada en la tarea cognitiva de conversión de las representaciones de tales conjuntos desde el registro gráfico hacia el registro algebraico.
Metodología
La secuencia didáctica a la que alude el presente artículo fue la base de una investigación que se desarrolló en el ámbito de la asignatura Álgebra A de la Carrera de Ingeniería de la Universidad Nacional de Mar del Plata, Argentina.
El enfoque de dicha investigación es mixto, es decir, que se realizan análisis tanto cuantitativos como cualitativos. Se usan herramientas de estadística inferencial para validar resultados y se realizan análisis interpretativos de los datos obtenidos de revisiones bibliográficas, de análisis de materiales didácticos, de resoluciones de estudiantes. Las hipótesis planteadas en la investigación la clasifican como un estudio de tipo explicativo. El objetivo general de la investigación fue explorar los resultados de la implementación de una secuencia didáctica orientada a favorecer la producción de conversiones desde el registro gráfico al algebraico, en subconjuntos de números complejos. Para la consecución de dicho objetivo se planificaron y ejecutaron las siguientes tareas (Aznar, Distéfano, Moler y Pesa, 2014):
Diseño de un instrumento para medir la habilidad de efectuar conversiones no congruentes desde el registro gráfico al registro algebraico en conjuntos de números complejos.
Elaboración de una secuencia didáctica para favorecer la adquisición de la habilidad de efectuar conversiones no congruentes desde el registro gráfico al registro algebraico en conjuntos de números complejos.
Selección de dos grupos de estudiantes que cursaran la materia Álgebra A. En uno de los cuales se aplicó la secuencia didáctica, y el otro fue de cuasi-control.
Administración del instrumento diseñado, en ambos grupos, a manera de pretest, luego del desarrollo de la unidad de números complejos en las clases prácticas.
Implementación de la secuencia didáctica en uno de los grupos.
Administración del instrumento de evaluación en ambos grupos, a manera de postest, después de la secuencia didáctica.
Analizar los datos obtenidos en ambos grupos, con base en el instrumento y en los puntajes obtenidos en los ítems correspondientes al tema números complejos de la evaluación parcial de la asignatura.
Se diseñó un instrumento conformado por seis ítems; dos de ellos pueden observarse en la Figura 1. En cada ítem se exhibe la representación gráfica de una curva o región del plano complejo determinada por una característica común sobre el módulo, la parte real o el argumento. En cada curva o región representada, cada estudiante debe identificar qué cualidad comparten los números complejos que la componen. Tal característica es la unidad significante que el estudiantado debe expresar en forma de una ecuación o una inecuación en el lenguaje algebraico. A cada ítem se le asignó un puntaje de 1 (uno) punto; en consecuencia, el puntaje máximo total obtenible en el instrumento es de 6 (seis) puntos.
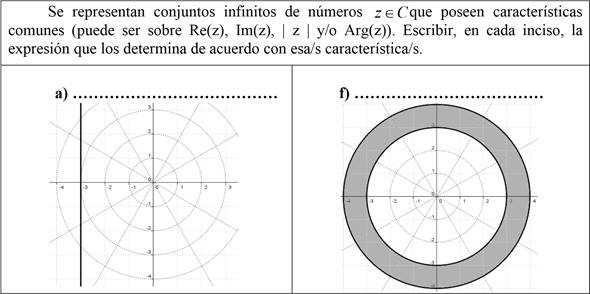
Figura 1 Enunciado y dos ítems de la Prueba de habilidad de conversión registro gráfico - registro algebraico. Fuente propia de la investigación.
Para poder realizar la conversión de una representación desde el registro gráfico al algebraico, el estudiantado debe lograr visualizar cuáles son las unidades significantes, y cómo están relacionadas. Así, por ejemplo, en el caso del ítem a), debe poder visualizar, en la recta vertical, infinitos complejos que comparten la característica visual de tener la misma proyección sobre el eje real y que esta vale -3. A su vez, debe poder expresar dicha característica, en el registro algebraico, como Re(z)= -3. En el caso del ítem f), para que sea posible la conversión, debe visualizar, dentro de esa región sombreada, infinitos complejos como vectores con origen en (0,0), con ángulos variables y, con módulos variables entre dos valores determinados por las dos líneas límite de la región. Debe identificar dichos valores y, finalmente, debe poder expresar en el registro algebraico esta relación como  .
.
La validez de contenido del instrumento fue determinada a través del juicio de tres de docentes a cargo de asignaturas del área Álgebra de la Universidad Nacional de Mar del Plata, en calidad de personal experto, que aportó sugerencias sobre la presentación de los gráficos. La confiabilidad del instrumento fue establecida a partir de los datos recabados de su administración a estudiantes ingresantes de las carreras de Ingeniería y de Ciencias Exactas y Naturales de la cohorte 2009. Los datos obtenidos se analizaron utilizando el paquete estadístico SSPS versión 15.0, y se obtuvieron coeficientes Alfa de Cronbach de 0,810 y 0,727, respectivamente. Estos son considerados como valores aceptables de coeficientes de consistencia interna (Hernández-Sampieri, Fernández-Collado y Baptista- Lucio, 2006).
En relación al objetivo se plantearon dos hipótesis específicas:
Hipótesis 1: El alumnado que participe de la implementación de la secuencia didáctica, fundamentada en la teoría de registros semióticos y orientada a favorecer la habilidad de efectuar conversiones no congruentes, desde el registro gráfico al registro algebraico, de conjuntos de números complejos, tendrá un nivel de logro de aprendizaje en ese tipo de conversiones significativamente superior al de quienes no participen de tal implementación.
Hipótesis 2: El alumnado que participe de la implementación de la secuencia didáctica tendrá un desempeño, en la resolución de problemas que impliquen representaciones de números complejos en los registros gráfico y algebraico, significativamente superior al de quienes no participen de esta.
La variable independiente en ambos casos es la implementación de la secuencia didáctica a la que estuvo expuesto uno de los grupos, entendida como un conjunto de actividades ordenadas, estructuradas y articuladas para la consecución de unos objetivos de aprendizaje.
La variable dependiente en la primera hipótesis es nivel de logro de aprendizaje concebido como el nivel de progreso en la habilidad de realizar conversiones desde registro gráfico al registro algebraico. Esta habilidad requiere de la identificación de las unidades significantes en una representación gráfica y la expresión de sus características en forma de ecuaciones o inecuaciones planteadas en el lenguaje algebraico. Esta fue operativizada, a partir de los puntajes obtenidos en el pretest (P1) y postest (P2), mediante el porcentaje en la diferencia de la habilidad: 
Para la segunda hipótesis, la variable dependiente es el desempeño en la resolución de problemas que impliquen representaciones de números complejos en los registros gráfico y algebraico; esa se asume como una expresión valorativa de la resolución de tareas referentes a números complejos, para las cuales el alumnado deberá emplear ambos tipos de representaciones. Fue operativizada, a partir del puntaje obtenido en los ítems del examen parcial que evaluaban dicho tema (PO), mediante el porcentaje ítems sobre números complejos: 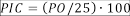
Se consideró como variable externa el nivel de conocimientos previos de matemática. Para evaluar dicha variable se tomó como indicador la calificación del Examen de ingreso a la Facultad. En este se evaluaron contenidos relativos a expresiones algebraicas, ecuaciones algebraicas y trascendentes, análisis de funciones, problemas de geometría analítica vinculados a recta, parábola, cónicas y problemas de trigonometría.
Se seleccionaron dos grupos de trabajo de clases prácticas que desarrollaban estas mismas en forma simultánea en aulas diferentes, en las cuales se administró el instrumento, a manera de pretest, al concluir el estudio de los temas vinculados a representaciones gráficas. Es importante señalar que al momento de la instancia pretest, si bien el alumnado había resuelto, en la guía de trabajos prácticos, numerosos ejercicios que implicaban conversiones desde el registro algebraico al registro gráfico, no había recibido ninguna formación específica en lo referido a la identificación de las unidades significantes en representaciones gráficas de conjuntos de números complejos para expresarlas a través de una condición, en forma binómica o en forma polar, en el registro algebraico. Posteriormente, en una de las comisiones se desarrolló la secuencia didáctica diseñada.
Dado que, según León y Montero (1997), el efecto de selección puede constituir una amenaza a la validez interna del diseño, se compararon ambos grupos, el experimental y el de cuasi-control, en dos variables: el puntaje obtenido por los alumnos en su examen de Ingreso y el puntaje obtenido en el Pre-test. Se compararon entre los grupos las distribuciones de la variable Ingreso a través de la prueba U de Mann-Whitney (U=216,5 y p=0,742) y de la variable Pre-test mediante la prueba t ( t=0,397 y p=0,693). A partir de las comparaciones efectuadas se determinó que los grupos puedan considerarse homogéneos, tanto desde el punto de vista de sus conocimientos generales previos de matemática como de sus conocimientos específicos en cuanto a las conversiones en estudio.
Luego de la implementación de la secuencia en uno de los grupos, se administró el mismo instrumento, en ambas comisiones, a manera de postest. También se registraron los datos de los puntajes en los ítems del examen de la asignatura en el que se evaluaron contenidos relativos a números complejos para poder medir el desempeño en la resolución de problemas que involucren las representaciones en estudio. Se pudieron obtener datos completos en 20 estudiantes del grupo experimental y 23 del grupo de cuasi-control.
Cabe acotar que, considerando el tamaño de las muestras, fueron testeadas las distribuciones de las variables estudiadas en ambos grupos mediante el Test de Shapiro-Wilk determinándose, como consecuencia de los valores obtenidos, la utilización de test no paramétricos para todas las variables a excepción de la variable pretest.
Para diseñar la secuencia didáctica se realizaron estudios previos para esbozar las instancias y aspectos involucrados en las tareas asociadas a este tipo de conversiones.
Por una parte, se efectuó un análisis de los resultados obtenidos a partir de la administración del instrumento diseñado a estudiantes de una cohorte anterior a la intervenida. La información obtenida (Aznar, Distéfano, Massa, Figueroa y Moler, 2010) permitió determinar dos aspectos fundamentales en la ejecución de estas tareas cognitivas: la identificación de las unidades significantes en los rasgos del gráfico y la formación de representaciones de acuerdo con las reglas de conformidad del registro algebraico.
Por otra parte, a partir del análisis del material didáctico y de la bibliografía utilizada por el estudiantado, se comprobó, en estos, la ausencia de propuestas de prácticas que requieran la actividad cognitiva de conversión desde el registro gráfico al algebraico. Asimismo, se observó en la bibliografía recomendada la presentación de representaciones en el registro gráfico sin elementos guía para facilitar su lectura: en su gran mayoría contenían esquemas gráficos donde se omiten las graduaciones en los ejes cartesianos con sus valores y tampoco aparecen líneas que orienten la visualización de los valores de los ángulos correspondientes a los argumentos o de la medida de los módulos.
A partir de los dos análisis mencionados se definieron algunos lineamientos a seguir para el diseño de la propuesta pedagógica:
Facilitar al estudiantado la lectura de los rasgos gráficos en el plano complejo. Para ello se deben hacer ostensibles la graduación del eje real y del eje imaginario y dotarlo de líneas auxiliares punteadas en forma de semirrectas o de circunferencias centradas en el origen para favorecer la identificación de valores de argumentos y módulos de números complejos representados.
Incluir actividades orientadas al logro de la identificación de las unidades significantes con sus valores.
Contemplar prácticas orientadas a la correcta expresión de sus características en el lenguaje algebraico respetando las reglas de formación de representaciones.
Graduar el nivel de dificultad que adquieren estas tareas.
A continuación, se describen la estructura de la propuesta didáctica, las variables didácticas que controlan el grado de dificultad de las actividades que la componen y cómo se implementó.
La propuesta didáctica se estructuró como una secuencia didáctica, entendida como un conjunto de actividades ordenadas, estructuradas y articuladas para la consecución de unos objetivos de aprendizaje (Zaballa-Vidiella, 1995). Fueron organizadas en bloques de apertura, desarrollo y cierre.
Bloque de apertura
Este bloque comprende la Actividad I, cuyo objetivo es promover la exploración de las reglas de formación de expresiones en el registro gráfico a través de las tareas que requieran:
identificar números complejos representados en el registro gráfico y realizar la conversión congruente de su representación al registro algebraico.
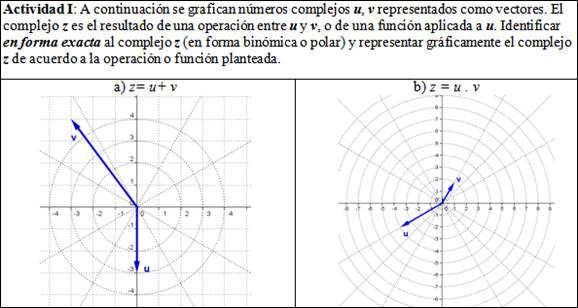
Representar, en el registro gráfico, un número complejo z obtenido como resultado de una operación entre dos números complejos dados.
El enunciado de esta actividad y algunos incisos se ilustran en la Figura 2. Para la resolución de esta misma, el alumnado debe hacer uso de conocimientos previamente desarrollados en la guía de trabajos prácticos. Consiste en resolver operaciones entre números complejos que, en lugar de estar expresados en el registro algebraico, están representados en el plano complejo; asimismo se le pide representar en dicho plano el número complejo z, resultado de la operación planteada en cada caso. Las conversiones entre el registro gráfico y el algebraico solicitadas, son congruentes. Esto, junto con los tratamientos requeridos por las operaciones, es acorde con la necesidad de partir de las actividades semióticas más desarrolladas hasta ese momento en la asignatura.
Bloque de desarrollo
Este bloque comprende las Actividades II y III.
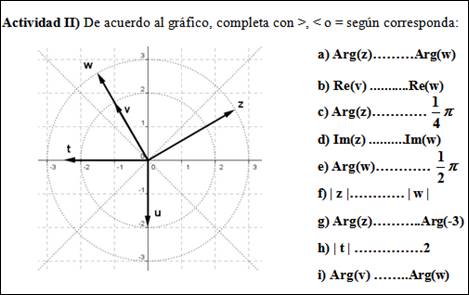
Con la Actividad II se pretende promover, en el estudiantado, la construcción parcial de expresiones, en el registro algebraico, que representen relaciones o características de elementos de números complejos representados en el registro gráfico.
En esta actividad, presentada en la Figura 3, se proporciona al alumnado un conjunto finito de números representados en el plano complejo. El ejercicio consiste en completar las expresiones algebraicas para caracterizar relaciones entre alguno de sus elementos: parte real, parte imaginaria, módulo o argumento principal. El alumnado debe convertir la relación gráfica a una relación expresada en lenguaje algebraico completando una línea punteada.
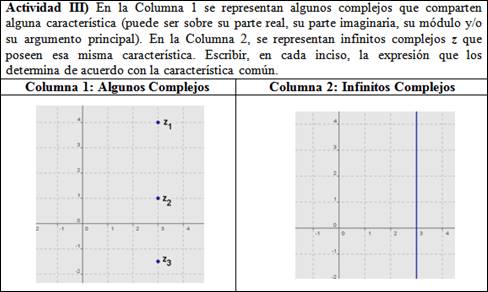
Con la Actividad III, se aspira favorecer en el estudiantado la inducción de una condición que caracteriza a conjuntos de infinitos números complejos representados en el registro gráfico a partir de la identificación de elementos particulares. Esta condición es la que luego debe expresar en el registro algebraico siguiendo lo trabajado en la Actividad II.
Como se ilustra en la Figura 4, se presentan, en dos columnas, conjuntos de complejos caracterizados por la misma condición. En la columna de la derecha aparece el conjunto representado con infinitos elementos, en la columna de la izquierda aparece un subconjunto finito del mismo conjunto. Se propone al estudiantado expresar la relación que caracteriza los elementos del conjunto dado.
La actividad propuesta tiene características de lo que Duval (1998) denomina una tarea de variación comparativa. En cada inciso, los rasgos gráficos que varían son las representaciones proporcionadas en la columna de la izquierda de los distintos complejos del subconjunto finito. De un número complejo a otro solo se cambia una variable visual por vez. Por ejemplo, en el inciso a) solo varía “la altura” y se mantiene fija la “distancia al eje vertical”. Los casos particulares mostrados en la columna de la izquierda se muestran asociados al caso general en la columna de la derecha. La conversión se transforma en un método para analizar, en cada representación gráfica, qué rasgos son significativos del conjunto.
Bloque de cierre
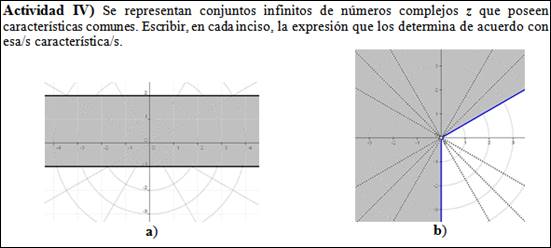
Comprende únicamente la Actividad IV que se muestra en la Figura 5. A diferencia de la actividad anterior, donde se le proporcionaba al alumnado un subconjunto finito como soporte, es el estudiantado quien debe identificar, dentro de la Gestalt del conjunto infinito, los elementos de este para caracterizarlos y expresar dicha caracterización representándola en el registro del lenguaje algebraico como síntesis de lo trabajado anteriormente en la secuencia.
En la teoría de situaciones didácticas se llaman variables didácticas a aquellas variables dentro de la situación que se presenta al estudiantado cuyo cambio le exige que modifique las relaciones que pone en juego en su interacción con la situación (Sadovsky, 2005). En este trabajo se toma y adapta esta idea considerando las variables que regulan el nivel de dificultad de conversión en las tareas propuestas.
Hay dos prácticas requeridas para poder efectuar la tarea de conversión planteada: la identificación de las unidades significantes en los rasgos del gráfico junto con sus valores y la formación de representaciones de acuerdo con las reglas de conformidad del registro algebraico. A partir de estas prácticas, se definieron variables que se identificarán como variables de conversión; las mismas caracterizan las actividades propuestas en la secuencia didáctica diseñada. Los distintos valores que adquieren las variables de conversión en las actividades modifican la forma en que el alumnado se enfrenta con las representaciones y varían el grado de dificultad de las prácticas matemáticas requeridas.
Las variables de conversión contempladas son:
Tipo de cardinal del conjunto representado. Las representaciones gráficas que se busca que el alumnado caracterice corresponden a conjuntos de números complejos que definen curvas o regiones en el plano complejo por lo que están conformados por infinitos elementos. Sin embargo, en algunas de las actividades planteadas en la secuencia, se presentan al alumnado algunos subconjuntos finitos y esto determina que la actividad cognitiva de conversión resulte más simple, pues tiene características de conversión congruente. Esto sucede porque se expone ante el alumnado un conjunto finito de puntos o vectores del plano complejo, en una representación convenientemente provista de líneas guía que facilitan la lectura de rasgos gráficos con sus valores. En consecuencia, los valores cualitativos que la variable cardinal del conjunto representado puede tomar son: finito unitario, finito no unitario e infinito.
Tanto en la Actividad I como en la Actividad II se presentan al estudiantado uno o varios números complejos que se pueden considerar, individualmente, como conjuntos finitos unitarios. En la Actividad III (ver Figura 4), esta variable adquiere dos valores distintos, pues la representación que se presenta en la columna izquierda tiene un conjunto finito no unitario de números complejos; se pretende usar esta representación como soporte para que el alumnado induzca la condición que caracteriza al conjunto de infinitos números complejos representado en la columna de la derecha. Finalmente, en la Actividad IV todos los conjuntos representados tienen cardinal infinito y esto representa el máximo nivel de dificultad.
Grado de construcción de la expresión en el registro algebraico. Las representaciones de las condiciones que caracterizan una curva o una región del plano complejo en el registro algebraico requieren el conocimiento de las reglas de formación de expresiones en dicho registro. En algunas de las actividades, el estudiantado solo tiene que identificar un número complejo singular por lo que no se le requiere escribir condiciones; en otras, se le proporcionaron, al alumnado, condiciones en forma de expresiones algebraicas parciales que debe interpretar y completar; finalmente, las actividades más complejas requieren que el alumnado represente en el registro algebraico la totalidad de la expresión que caracteriza al conjunto. Los valores cualitativos que la variable grado de construcción puede adquirir son: nulo, parcial y total.
En la Actividad I, el grado de construcción es nulo ya que, no se requiere expresar una condición que caracterice elementos, únicamente representar el resultado de una operación. En la Actividad II es parcial, porque que el alumnado ya dispone de las componentes expresadas en dicho registro y debe completar con la simbolización de la relación. En las actividades III y IV el grado de construcción requerido es total, ya que el alumnado debe materializar totalmente la formación de la representación de la regularidad observada, en el registro algebraico.
Cardinal del conjunto de valores que toma la unidad significante. Las curvas o regiones del plano complejo que se utilizan en este trabajo están caracterizadas por los valores que toma su parte real, su parte imaginaria, su módulo o su argumento. Las representaciones de cada uno de estos elementos son las llamadas unidades significantes. En el registro algebraico las unidades significantes serían los rasgos asociados a las expresiones Re(z), Im(z), Arg(z) y | z |. Así, la curva representada en el lado izquierdo de la Figura 6 se puede entender como el conjunto de los z(C / | z |=2, es decir, el módulo, como unidad significante, toma un único valor que es 2. En cambio, en la parte derecha de la figura, la región se puede definir como el conjunto de los z(C / 3(| z |( 4, lo que implica que el conjunto de valores que puede tomar el módulo corresponde a un conjunto de infinitos valores reales positivos pertenecientes al intervalo [3; 4]. Esta condición de infinitos valores dificulta tanto la identificación en el gráfico como su expresión en el registro algebraico. Por lo anteriormente expuesto, se definieron dos valores cualitativos para la variable cardinal: finito unitario e infinito.
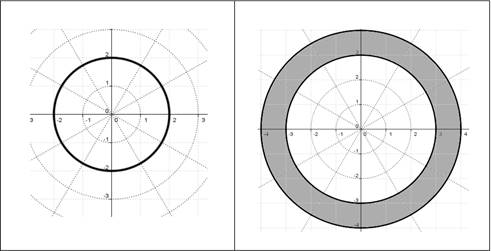
Figura 6 Ejemplificación de conjuntos de valores que toma la unidad significante. Fuente propia de la investigación.
En las Actividades I y II, la variable carece de valor puesto que no hay curvas o regiones representadas. En la Actividad III adquiere dos valores diferentes: es finito unitario en los incisos a) y b) e infinito en los restantes incisos, ya que los valores que adquiere la unidad significante conforman intervalos reales. En la Actividad IV, el cardinal de los valores de la unidad significante es infinito en todos los incisos.
En la Tabla 1, se muestran los valores de cada variable didáctica en las actividades de la secuencia. El símbolo ( marca el valor alcanzado por cada actividad; el sombreado más oscuro indica mayor nivel de dificultad. Puede observarse que, correlacionado con el orden de la actividad dentro de la secuencia, aumenta el nivel de dificultad de esta.
Tabla 1 Valores de las variables de conversión en cada actividad de la secuencia
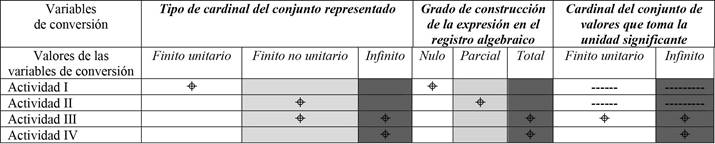
Nota: Fuente propia de la investigación.
La propuesta didáctica fue implementada luego del habitual desarrollo de los temas relativos a representación polar y a representación gráfica de conjuntos de números complejos. En particular, de aquellos conjuntos caracterizados por condiciones sobre su parte real, su parte imaginaria, su módulo, su argumento o combinaciones de ellas; que configuran tareas presentes en la guía de trabajos prácticos de la materia. Se debe notar que, si bien en estos ejercicios trabajados en la práctica habitual de la asignatura se hace uso del registro gráfico, el sentido de la conversión usada es desde el registro algebraico hacia el gráfico y, el sentido de conversión que se busca favorecer en la secuencia propuesta es el opuesto.
La secuencia tuvo lugar en una de las comisiones de estudiantes durante la clase de trabajos prácticos de 2 horas de duración. La modalidad seleccionada para el desarrollo de esta propuesta fue la dialógica. Docentes observadores señalaron que se logró el diálogo entre los distintos actores en la clase verificándose en estudiantes, a lo largo de la clase, niveles altos de atención y medianos-altos de participación.
Resultados
A continuación, se describen los resultados de esta experiencia distinguiendo entre ellos los correspondientes a comparaciones cuantitativas entre los grupos de estudiantes considerados, los hallazgos didácticos realizados durante la implementación de la secuencia y las voces de estudiantes que participaron en ella.
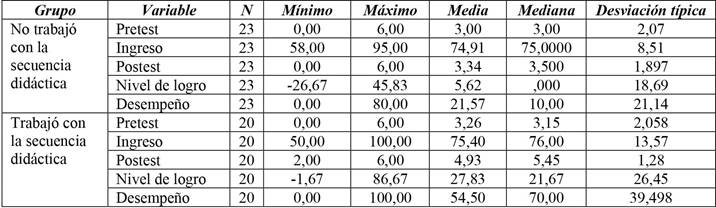
Se realizó un análisis descriptivo de los datos, estableciendo medidas centrales (media y mediana) y de dispersión (desviación típica) de las variables involucradas en la investigación como así también de las que provienen de las mediciones parciales que se muestran en la Tabla 2.
Con el objeto de evaluar los resultados de la implementación de la secuencia didáctica orientada a favorecer la habilidad de efectuar conversiones no congruentes desde el registro gráfico al registro algebraico, de representaciones de conjuntos de números complejos, se compararon en ambos grupos tanto la calificación en el postest (P2) como en el nivel de logro de aprendizaje operativizado a través del porcentaje en la diferencia de la habilidad (PDH).
Las pruebas U de Mann-Whitney de comparación de medianas para las variables postest y arrojaron los siguientes valores:
Postest (P2): U=113,000 y p=0,04
Porcentaje en la diferencia de la habilidad (PDH): U=111,000 y p=0,04
Los resultados de la comparación de las variables asociadas al postest y al nivel de logro indican que se observan diferencias estadísticamente significativas (p <0,05) entre el alumnado que participó de la implementación de la secuencia y el que no participó. Para el grupo no intervenido, las medianas de las variables postest y nivel de logro fueron, respectivamente 3,5 y 0; para el grupo intervenido, las medianas de las variables postest y nivel de logro fueron 5,45 y 21,67 respectivamente. Estos valores indican que son mejores los resultados obtenidos en el grupo que participó en la intervención y permite afirmar que esta causó el impacto esperado sobre estudiantes que participaron de ella.
Para evaluar los resultados de la implementación de la secuencia didáctica sobre el desempeño en la resolución de problemas referentes a números complejos, se analizó la variable desempeño, operativizada a partir de las notas obtenidas en los ítems del examen en el cual la cátedra evaluó, entre otros, el tema números complejos. Es importante señalar que la resolución de dichos ítems demanda efectuar las mismas prácticas matemáticas requeridas en la guía de ejercitación de la asignatura. Para desarrollar dichas prácticas, las actividades semióticas involucradas son tratamiento en el registro algebraico y conversión en el sentido registro algebraico ( registro gráfico, que fueron las habitualmente trabajadas en la asignatura.
La prueba U de Mann-Whitney de comparación de medianas para la variable desempeño arrojó los siguientes resultados: U=115,000 y p=0,004. Esto indica que se observan diferencias estadísticamente significativas (p < 0,05) entre estudiantes que participaron de la implementación de la secuencia didáctica y quienes no participaron. Los valores de las medianas, fueron 10 para el grupo que no participó y 70 para el que participó; estos valores indican que son mejores los resultados obtenidos en el grupo que participó en la implementación de la secuencia didáctica.
Los resultados cuantitativos expuestos dan cuenta de efectos beneficiosos de la implementación de la secuencia didáctica sobre la habilidad de conversión en estudio y sobre el desempeño en la evaluación, que puede entenderse como una manifestación parcial de la conceptualización de los números complejos.
Resultados cualitativos
Desde el punto de vista cualitativo, pueden señalarse resultados provenientes de la puesta en juego de la secuencia didáctica.
La modalidad dialógica con la que se implementó la secuencia didáctica permitió la detección de algunos conflictos semióticos. Estos son definidos por Godino, Batanero y Font (2009, p. 15) como “cualquier disparidad o discordancia entre los significados atribuidos a una expresión por dos sujetos (personas o instituciones)”. Un ejemplo de ellos se manifestó, en el inciso b) de la Actividad II, ya expuesta en la Figura 3, en el que debían completar la expresión Re(v)...........Re(w), correspondiente a la comparación de las partes reales de los números complejos v y w. Algunos estudiantes consideraron erróneamente que la parte real de w es mayor que la de v. Esto podría deberse a que interpretaran una relación del tipo “a mayor módulo mayor parte real”, que solo es válida cuando las partes reales de ambos complejos son positivas. Podría aducirse que identifican como rasgo significativo “la longitud de la flecha”.
La revelación de estos conflictos semióticos es en sí misma un resultado que, por una parte, posibilitó alertar y procurar en el momento su resolución con el alumnado y, por otra parte, induce a modificaciones en los materiales o trayectorias didácticas futuras con el fin de prevenirlos.
La implementación de la secuencia didáctica fue planteada al alumnado participante como una tarea de repaso adicional en el contexto de las clases de consulta. Al final de la secuencia se le solicitó al estudiantado que escribiera una breve frase sobre su parecer acerca de la utilidad o no utilidad de las actividades desarrolladas. En general, consideró que la secuencia le resultó de utilidad y tuvo valoraciones positivas. En algunos casos expresaron que les ayudó a “afianzar”, “integrar” o “tener más claros” los conceptos. Estas expresiones hacen alusión a la conceptualización o noesis. Es decir, que una actividad que estuvo fuertemente ligada a la semiosis fue valorada por el alumnado como favorecedora de su comprensión conceptual. Esto es coherente con las afirmaciones que Duval (1998, 2004) realiza acerca de la necesidad de la semiosis para la noesis.
Conclusiones
En esta investigación se partió de considerar la relevancia de la habilidad de simbolizar algebraicamente curvas o regiones representadas en el plano complejo. Dicha relevancia fue planteada desde dos puntos de vista: por la necesidad de esta habilidad para resolver ciertos problemas y por implicar un recorrido cognitivo necesario para completar la coordinación entre los registros algebraico y gráfico, señalada como condición ineludible para la conceptualización. El desafío consecuente fue el diseño de una secuencia para favorecer esa habilidad.
El diseño estuvo estructurado considerando dos prácticas requeridas para poder realizar este tipo de conversiones: la identificación de las unidades significantes en los rasgos del gráfico junto con sus valores y la formación de representaciones de acuerdo con las reglas de conformidad del registro algebraico. A partir de la diferenciación de condiciones para estas prácticas se definieron valores de variables de conversión. Estos valores fueron tenidos en cuenta para el diseño de las actividades, con el objetivo de graduar el nivel de dificultad de las tareas de conversión requeridas a lo largo de la secuencia.
La conversión en el sentido registro algebraico ( registro gráfico era trabajada habitualmente en las prácticas matemáticas realizadas en la cátedra. La implementación de la secuencia didáctica adicionó el trabajo de actividades para favorecer las conversiones en sentido inverso: registro gráfico ( registro algebraico. Es decir, el estudiantado participante de la implementación de la secuencia didáctica trabajó ambos sentidos de conversión, necesarios para la coordinación entre ellos.
Aunque el tamaño de las muestras limita la generalización de los resultados cuantitativos obtenidos, estos y las opiniones de estudiantes participantes señalan que la secuencia didáctica propuesta no solo favoreció las conversiones a las que buscó específicamente contribuir, sino también coadyuvó en prácticas matemáticas que requieren otras actividades semióticas vinculadas a representaciones de números complejos en los dos registros considerados. Dado que la conceptualización o construcción de significados matemáticos puede traducirse en términos de acciones cognitivas de formación, tratamiento y conversión (D’Amore, 2011), puede expresarse que, al menos parcialmente, hay una manifestación de mayor conceptualización de los números complejos en el grupo que participó de la secuencia didáctica.
La secuencia didáctica que se expuso en este trabajo estuvo restringida a los recursos temporales y materiales disponibles. Podría ser de interés estudiar los efectos de un abordaje didáctico con tareas de conversión trabajadas con el soporte de un software de geometría dinámica, lo cual requeriría una cuidadosa determinación de los registros de representación en juego. Por otra parte, también se podría estudiar la efectividad de actividades como las propuestas, aplicadas a otros objetos matemáticos que admitan representaciones en los registros algebraico y gráfico. En este sentido, se espera que la definición de variables de conversión pueda ser útil para el abordaje de este tipo de diseños didácticos.