Small-scale fisheries contribute a high percentage to the global fisheries and are a means of livelihoods for several million people, particularly in developing countries where other livelihood options are often very limited. However, over the past decades, several fish stocks have been showing a declining trend due to overfishing (Pauly, Christensen, Dalsgaard, Froese, & Torres, 1998; Froese, 2004; Winker, Weyl, Booth, & Eilender, 2011; Hicks & McClanahan, 2012), and their proper assessment and management seem imperative to sustain their fisheries and the benefits for the society. Information on the ecology and life histories of the fish stocks are prerequisites for fisheries management. Stock assessment comprises the study on the population dynamics controlled by growth, recruitment, natural and fishing mortalities (King, 1995). Fish stocks decrease in size when the gains from spawning, recruitment and individual growth are smaller than the losses from natural and fisheries mortality. The main cause for natural mortality is generally predation, but other factors such as starvation, diseases, dramatic environmental fluctuations like oxygen depletion, increase/decrease water temperature and other water quality parameters may also be influential. Adverse environmental conditions could result from deforestation, pollution (both point and non-point source), eutrophication and other land-based anthropogenic activities. Fisheries always induce an additional mortality to the stock, which needs to be balanced through an increase in biomass production by the stock, if the fishery is to be sustained. To understand the species response to ecosystem manipulation or perturbations, to analyze economic impacts of changes in their population sizes over time and to carry out population viability and Maximum Sustainable Yield (MSY) analysis, it is necessary to study the population dynamics of the stocks under the current exploitation regime.
Lake Koka fisheries have been developing over the past decades and the lake was part of the eight major lakes considered by the lake fisheries development project (LFDP) in 1990s (LFDP, 1997). Koka is among the most important lakes for Ethiopian small scale fisheries in general and riparian societies in particular (Tesfaye & Wolff, 2014). At present it provides about 625t of fish annually. The commercially important species include tilapia Oreochromis niloticus (Linnaeus, 1758), catfish Clarias gariepinus (Burchell, 1922), common carp Cyprinus carpio (Linnaeus, 1758), and barbs Labeobarbus intermedius (Ruppell, 1835) (LFDP, 1997). Of these, O. niloticus, C. gariepinus and C. carpio comprise more than 95 % of the annual catch. Our study, therefore, focused on these three target species assuming that the fishing pressure might be high and regulative measures might be needed. The biology and ecology of these species have been studied in different water bodies in Ethiopia (Admassu, 1996; Tadesse, 1997; Wudneh, 1998; Tadesse, 1999; Dadebo, 2000; Teferi, Admassu, & Mengistou, 2004; Tesfaye & Tadesse, 2008). The growth of these species has also been reported in other areas, but very little is known about their vital population parameters and exploitation status in Lake Koka. Only for O. niloticus, LFDP (1997) and Tesfaye (2006) reported preliminary estimates of vital population parameters in Lake Koka. In the study here presented we aimed at determining the growth and mortality parameters and the stock status of the three fishery target species in Lake Koka following two complementary approaches: (1) estimating mortality parameters (Z and M) from catch curves and empirical formulas, respectively, to calculate the exploitation rate (E) and comparing its value with a proposed index by Gulland (1971), and (2) using size indicators i.e., assessing the size distribution of the fish catches relative to the size at maturity (L m), and relative to the size that provides maximum cohort biomass and hence, maximum yield per recruit (L opt) and to the abundance of mega-spawners. The results of the study are expected to serve as inputs to fisheries models and management decisions aimed at the determination of the optimum level of exploitation of the target resources.
Materials and Methods
Study area: The tropical Lake Koka (also called Lake Galilea in the past) is located in the Ethiopian Rift Valley (08°23'22" N - 39°05'15" E) at an altitude of 1 590 m.a.s.l., about 90 km Southeast of Addis Ababa. It has a surface area of about 255 km2 with a maximum and mean depth of 14 m and 9 m, respectively (Vanden, Bossche, & Bernacsek, 1991; LFDP, 1997). Water in- and outflow is mainly provided by the Awash River. In addition, the Mojo River may also generate inflow during the rainy season. The lake has a large floodplain area in its Western side. The climate is characterized by a four-months dry season (November-February) and an eight-months rainy season (March-October) (Gamachu, 1977). The total annual rainfall varies from 600-800 mm in the Rift Valley area (Ayenew, 2004) and the mean annual temperature ranges from 20-26 oC (an average of about 23 °C) (Degefu, Teshome, Tesfaye, Tefera, & Lakew, 2011). The pH of the water ranges from 8-9 and conductivity from 200-393 LiS/cm (Mesfin, Tudorancea, & Baxter, 1988; Degefu et al., 2011). The Secchi depth of Lake Koka is low and on average ranges from 12-28 cm due to suspended silt coming in by the River Awash (Kebede, Zinabu, & Ahlgren, 1994; Degefu et al., 2011). Sediments are very fine, easily washable through a 200 Lm mesh net, and the organic content is rather high when compared to other tropical African lakes described by Mesfin et al. (1988). Its chlorophyll a content is changing over time and reported figures include: 13.5 Lig/L (Kebede et al., 1994), 22.4 Lig/L (Mesfin et al., 1988) and 214.1 Lig/L (Degefu et al., 2011). Other chemical and limnological features were also studied by (Mesfin et al., 1988; Kebede et al., 1994; Tudorancea, Zinabu, & Dadebo, 1999; Zinabu, Kebede, & Desta, 2002).
Sampling and data collection: Length frequency data was taken from the commercial catches on a quarterly basis from 2007-2012 at the landing sites (Denbela and Tannery, Algaworash and Bridge, and Tsebel and Gefer-sa) and a total of 20 097 fish specimens (distributed as 7 933 tilapia, 6 025 catfish and 6 139 common carp) were measured. The common fishing gears used in Lake Koka fishery include beach seines with 60 mm mesh size codend, gillnets having 100 mm mesh size, and longlines with hook sizes ranging from 4/0-6/0 but beach seine catches contribute about 60 % to the annual landings. The total lengths (TL) of tilapia and catfish and the fork lengths (FL) of carp were measured to the nearest 0.1 cm and thereafter, these length type measurements were used in all subsequent analysis for the respective species.
Growth determination: Length frequency data obtained from the catches were used to determine the growth parameters. The growth of the fish species considered in the study was assumed to follow the von Bertalanffy growth function (VBGF):
Lt = Zoo*(1 - eK(t - to)) (1)
where, L t is the length at a particular given time, L x is the asymptotic length of fish in cm, K is the rate at which length approaches the asymptote, also called growth curvature, t is time (age) and t o is the theoretical age at which fish would have had at zero length, if fishes had grown according to VBGF. An estimate of t o was calculated using Pauly (1979) empirical equation:
log(-to) = -0.3922 - 0.275*logLoo - 1.038*logK (2)
VBGF Parameters (LM and K) were determined using the FiSAT II software (FAO-ICLARM Stock Assessment Tool II), a computer program package developed mainly for the analysis of length frequency data, but which also enables related size-at-age and catch-at-age analysis, as well as gear selection and other analysis (Gayanilo, Sparre, & Pauly, 2005). ELEFAN I, a routine in FiSAT II, was used to identify the growth curve that "best" fits a set of length-frequency data, using the value of the goodness of fit index (Rn) as a criterion (Gayanilo et al., 2005). L x and K values with the highest Rn values were then considered as "best" estimates.
Since ELEFAN does not provide confidence intervals for the growth parameter estimates, we employed the jackknife technique to drive a set of different L x and K estimates which then allowed us to calculate the mean and 95 % confidence interval (CI) of the estimates. The jackknife or "leave one out" technique, first developed by Quenouille (1956) and further expanded by Tukey (1958, 1986), has been used as a cross-validation technique to estimate the bias of an estimator (population parameter). It is an iterative process whereby a sample is omitted sequentially with replacement and generates a group of n samples with n - 1 data set and the estimate from this n - 1 sample called a partial estimate or also called a jackknife replication (Abdi & Williams, 2010). This technique has been used to quantify the effect of input data variations in growth parameter estimates (Levi, Andreoli, & Cannizzaro, 1987; Leonce-Valencia & Defeo, 1997; Flores, 2011; Arellano-Torres, Hernández Montaño, & Meléndez Galicia, 2013). Similarly, our growth analysis was performed using the length frequency data collected from 2010-2012 on a quarterly basis (but one quarter was missed in 2010), and thus, a total of 11 combinations of growth parameters (Loo and K) were obtained from each n -1 independent samples using the ELEFAN I - method. The coefficient of variation (CV) and the percent error (PE) were also calculated as a measure of precision. PE was computed according to Leonce-Valencia and Defeo (1997):
PE = ((St - St) / St ) *100 (3)
where St is the growth parameter estimate (Lo and K) using the whole data set (without jack-knife), and St is the mean parameter estimate obtained from the jackknife "pseudo - values". PE is optimum when it equal 0 (St = St). From those parameters, we also calculated the Phi prime (^') index (Munro & Pauly, 1983) used to compare the growth performance of fish in length, which is defined as:
0 = logK + 2*logLoo (4)
where, K and L x are growth parameters from VBGF. The length at optimum cohort biomass or yield per recruit (L opt) was calculated by Beverton (1992) as:
Lopt = L"* (3/(3+M/K)) (5)
where, L x and K are as defined above and M is the natural mortality coefficient.
We used our L m (Length at first maturity) estimates (Tesfaye & Wolff, unpublished) and computed the numeric percentage of specimens in the catches larger than L m. The percentage of fish between L m and L opt + 10 % larger sizes referred as the L opt range was then also calculated as well as the percentage of fish beyond this L opt range, referred to as mega - spawners (modified from Froese, 2004) (Fig. 1). These values were used as size indicators to evaluate the status of the targeted stocks.
Mortality and exploitation rates: Total instantaneous mortality (Z) was computed from a linearized length - converted catch - curve as described by Pauly (1984) and Gayanilo et al. (2005):
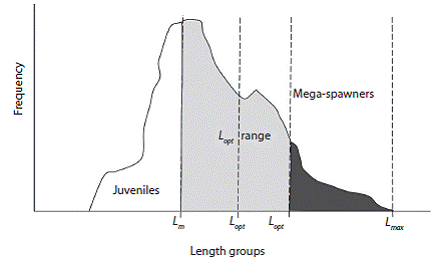
Fig. 1: Relative position of size indicators in a given fish catch. Light gray color refers the L opt range; dark gray color refers the Mega-spawners.
ln(NVAt) = a + b* L (6)
where N i is the number of fish in length class i, At is the time needed for the fish to grow through length class i, t i is the age (or the relative age) corresponding to the mid length of class i, and b, with sign changed, is an estimate of Z.
At = -(1/K)*ln((Loo - Li+J)/(Loo - L) (7)
and t i = -(1/K)*ln(1 - (L/L°o)) + to (8)
where, L i is the midpoint of length class i.
This approach assumes that Z is constant beyond some reference age, and thus we only considered individuals that are fully recruited or vulnerable to the fishing gear. The age of individuals fully recruited to the fishery is given by the point when the catch curve begins to decline at a steady rate and the corresponding length refers to the length at first capture Lc (Pauly, 1984). Z was therefore calculated by the regression line on individuals beyond this point (Pauly, 1984; Hicks & McClanahan, 2012).
The natural mortality coefficient (M) was estimated by two different empirical models proposed by Pauly (1980) and Rikhter and Efanov (1976) and used separately for further analysis. Pauly's formula relates M to the VBGF parameters and the mean annual water temperature and the formula is given as follows:
logM = -0.0066 - 0.279logLoo + 0.6543logK + 0.463T (9)
where, L x and K are VBGF parameters and T is mean water temperature in °C.
Rikhter and Efanov (1976) relate M to the age at which 50 % of the population matures (t m); a value corresponding to L m and their equation is given as follows:
M = 1.521/t/72 - 0.155 (10)
The L m values were converted into t m using equation 8. Since Z = M+F, fisheries mortality (F) was calculated by subtracting M (obtained using equation 9 and 10) from Z. The fisheries exploitation rate (E) was then calculated using each F estimates as ratio of F to Z (Gulland, 1971). E close to 0.5 is considered to describe an optimal level of exploitation, whereas E > 0.5 refers to a state of over exploitation.
Results
The Loo and K estimated for the whole data set and for the jackknife subset of data were slightly different. As seen in figure 2 , the Loo estimate for O. niloticus, C. carpio and C. gariepinus varied from 42.6-47.1 cm (2.9 %), 70.6-77.2 cm (2.6 %) and 118.2-126.1 cm (2.0 %), while K ranged from 0.32-0.41/year (11.3 %), 0.25-0.34/year (10.7 %) and 0.12-0.18/ year (13.9 %), respectively. For all species, both parameters were significantly correlated (O. niloticus: Pearson, r = -0.983, P < 0.05; C. gariepinus: Pearson, r = -0.898, P < 0.05 and C. carpio: Pearson, r = -0.686, P < 0.05). Table 1 shows the mean and 95 % CI of the estimated growth parameters, precision and goodness of fit estimates. Previously reported estimates are also presented in Table 2 for the purpose of comparison.
The best fitted growth curves using mean growth parameters as derived from the jack-knife method are shown in figure 3. Figure 4 shows the size spectrum for the three target fish species analyzed. The minimum and maximum lengths were 18 cm and 42 cm for O. niloticus, 25 cm and 121 cm for C. gariepinus, and 19 cm and 71 cm for C. carpio, respectively (Fig. 4 left). Lc, which is the lower limit of a size class completely selected and / or fully recruited (starting point of the catch curve, Fig. 5) and other life history characteristics are given in Table 3. The length-converted catch curves used to estimate the instantaneous total mortality rate are shown in figure 5, the estimates for the rates of natural and fishing morality and the derived values of the exploitation rates of these three species are summarized in Table 4.
Table 1: Growth parameters of O. niloticus, C. carpio and C. gariepinus from Lake Koka, estimated without (St) and with jackknife (Y); precision and ELEFAN goodness of fit estimates are also presented
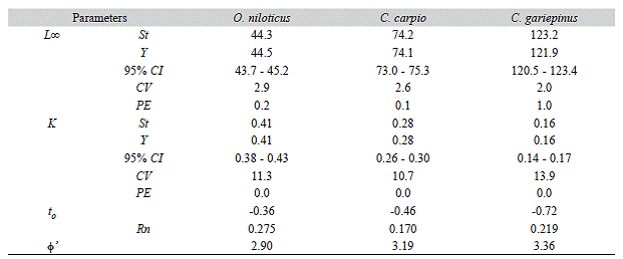
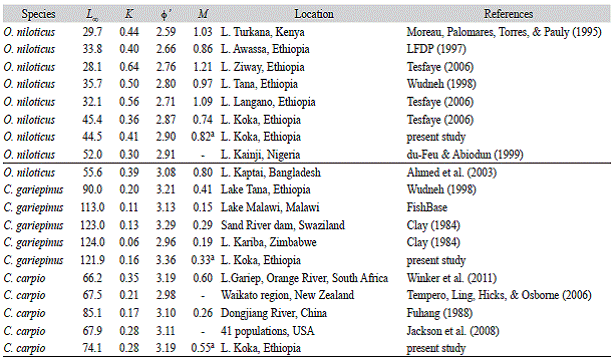
Table 2: Literature information on von Bertalanffy growth parameters and the rate of natural mortality for O. niloticus, C. gariepinus and C. carpio from different locations
Discussion
As has been pointed out by several authors, it is possible to determine daily growths in tropical fishes with modern aging techniques, however, growth determination through hard structures is often still difficult in tropical countries as it is time consuming, costly and the research equipment is often not available (Pauly, 1984; Sparre & Venema, 1998; Gayanilo et al., 2005). In Ethiopia, this is also exacerbated by an unwillingness of fishers to allow dissecting their fish for hard part extraction as they often sale whole fish. Thus, length frequency analysis remains the most viable and still most often used method for growth studies in tropical fish stock assessment. Leonce-Valencia and Defeo (1997) also suggested based on their comparative studies that length-based methods can also provide as accurate growth estimates as the time consuming directs methods. Once the growth parameters in length are obtained, it is possible to convert length into age using the inverse VBGF and into weight using the length - weight relationship. We thus, used length frequency data of the fish catches for determination of growth parameters.
The jackknife technique allowed us to quantify the effect of input data variations and uncertainty in growth parameter estimates. The two precision measures consistently showed low values of PE and CV for both L and K estimates for all the species considered. For a tilapia sister species in Mexico (Oreochromis auereus), Arellano - Torres et al. (2013) reported a slightly wider range of L o and K estimates 33.7-45 cm and 0.26-0.60/year, respectively using a similar jackknife analysis. However, in both studies the CV and PE of L (2.2 %; 0.7 %) and K (8.6 %; 14.7 %) estimates obtained using with and without jackknife technique were very similar. The inverse relationship between L o and K values also holds true in this study.
The growth parameters L o and K were different among the three species studied in Lake Koka but comparable to other studies. The rate at which fish size approaches L o is fastest in O. niloticus followed by C. carpio than C. gariepinus. It is also widely accepted that maximum size and the rate at which it is approached are highly interlinked in fishes with the result that most small fishes have fast growth, early maturation and short lives (r - selection traits), while most large fish species have slow growth, late maturation and long lives (K - selection traits) (Gulland, 1971; Ricker, 1975). Previous studies indicated that growth parameters could also differ for stocks within the same species depending on environmental conditions (Lowe-McConnell, 1982; Sparre & Venema, 1998). Intra - specific comparison of non - linear growth functions by their parameters L o and K were shown to be less meaningful (since they may vary even for the same species from different areas), whereas the use of the growth performance index 0' was shown better suited for comparing growth intra-and interspecifi-cally since it integrates over both descriptors of the growth curve (Munro & Pauly, 1983; Pauly & Munro, 1984).
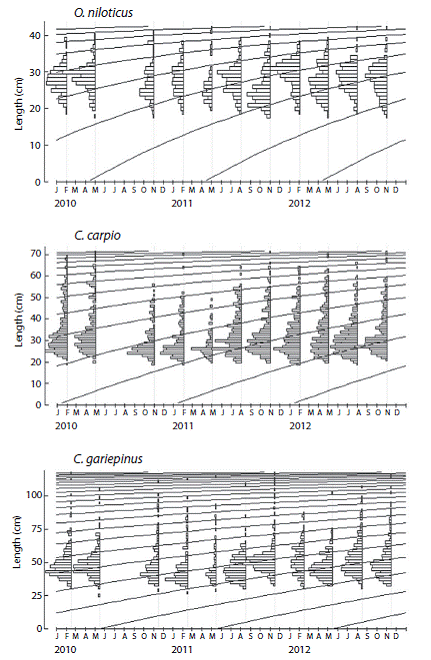
Fig. 3 von Bertalanffy growth curves of fishery target species in Lake Koka derived from the ELEFAN analysis with the mean of jackknife estimates.
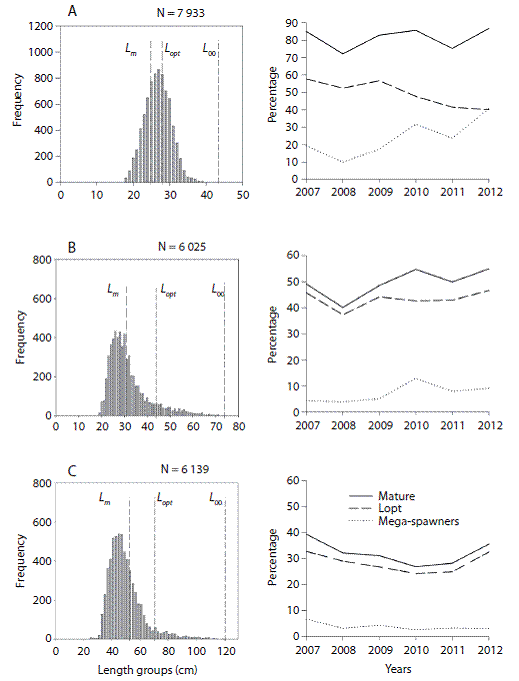
Fig. 4: Size spectrum (left) and time series of size indicators (right) for A) O. niloticus, B) C. carpio and C) C. gariepinus in Lake Koka.
Table 4: Mortality and exploitation rates of the fishery target species in Lake Koka
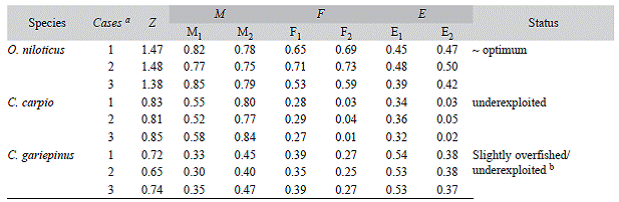
a Case 1 refers estimates computed using the mean value of Lm & K values, case 2 refers estimates computed using upper 95% CI of Lm & lower K and case 3 using lower 95% CI of Lm & upper K. b Ej for C. gariepinus indicated state of overfishing, but E 2 showed state of under exploitation. Abbreviations: Z = total mortality (year-1), M = Natural mortality (year-1); M 1 = Natural mortality obtained using equ. 9; M 2 = Natural mortality obtained using equ.10; F = Fishing mortality (year-1); F j = Z - Mj; F2 = Z - M2 ; E = Exploitation rate; E j = F/Z; E2 = F2/Z.
Our estimate of 0' for O. niloticus in Lake Koka was higher than that reported by LFDP (1997) but similar to the one reported by Tesfaye (2006). The calculated mean ± standard deviation of 0' -values for 36 O. niloticus, 30 C. carpio and 27 C. gariepinus populations reported in FishBase (excluding estimates from aquaculture facilities) (www.fishbase.org "Accessed 15 July 2014") are 2.68 ± 0.27, 3.07 ± 0.23 and 3.29 ± 0.20, respectively. Thus, our 0' estimate obtained for O. niloticus, C. carpio and C. gariepinus are well within these ranges and thus comparable with other studies. This suggests that our growth parameter estimates are reliable. Moreau, Bambino and Pauly (1986) compared the growth performance of 100 tilapia populations with different kind of growth performance indices and found that 0' is the best index for performance comparison. They found the best growth performance of O. niloticus in Lake Kainji, Nigeria and the worst in O. mossambicus from Lake Sibaya, South Africa. Apparently, the O. niloticus population from Lake Koka tends to grow better than populations in other Ethiopian lakes and Lake Turkana, and resembles that of the Lake Kainji, Nigeria population and the one with the slightly smaller index in Lake Kaptai, Bangladesh. Comparative studies in pond experiments on the growth performance of O. niloticus from Lake Koka and other Ethiopian lakes (Ziway, Awassa and Hora) also confirmed the better growth of O. niloticus from Lake Koka compared to other populations investigated (Work-agegn & Gjoen, 2012), which further confirms the reliability of our growth parameters estimate. Reliable estimates of 0' from wild stocks (as in the case here presented) could thus be used for the selection of species or populations for transfers and introductions (Moreau et al., 1986).
C. gariepinus from Lake Koka seems to reach larger sizes than in Lake Tana (L o is higher by more than 30 cm), but both populations showed similar performance indices. The estimated growth parameters for C. carpio are also very similar to the estimates reported for 41 populations in USA (Jackson, Quist, & Larscheid, 2008).
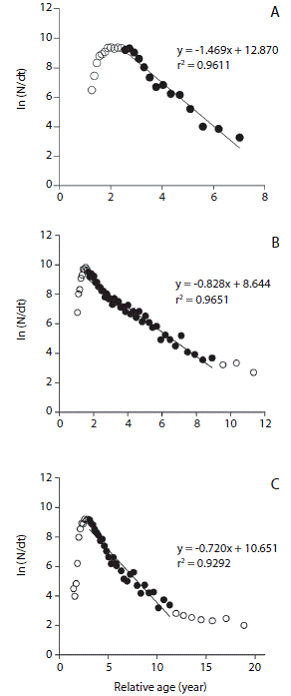
Fig. 5 Length-converted catch curves for A) O. niloticus, B) C. carpio and C) C. gariepinus in Lake Koka. Open circles (unused data points) represent individuals not fully recruited or juveniles (left side of the curves) & big adults not fully vulnerable by the fishing gear (right side of the curves) (see discussion).
Growth and mortality rates are very much interrelated. Growth affects the fish's vulnerability to both predation and fishing and it largely determines the food requirements of each individual fish (Allen & Hightower, 2010). And it is the growth of individual fish that provides the catch and prey potential for the fishery and the natural predators (Pauly, 1984). Pauly's empirical formula has been intensively used for the determination of natural losses (M) (Sparre & Venema, 1998; Ahmed, Amin, Haldar, & Dewan, 2003; Gayanilo et al., 2005). It assumes that small and fast growing fishes have higher natural losses (more predators), and that natural mortality also increases with environmental temperature (Pauly, 1980). Correspondingly, our smallest and fastest growing fish (O. niloticus) showed a higher M value than the other two larger species. In a parallel study, we observed that specimens of O. niloticus as well as their eggs and/or scales are commonly found in the gut of C. gariepinus in Lake Koka (Tesfaye & Wolff, unpublished). Similarly, previous studies confirmed O. niloti-cus to be an important prey for C. gariepinus in different water bodies (Dadebo, 2000; Dadebo, Aemro, & Tekle-Giorgis, 2014). For this reason, C. gariepinus is used in many countries as predator in tilapia-catfish poly-culture to control unwanted tilapia fries (De Graaf & Janssen, 1996; Solomon & Boro, 2010; Ibrahim & Naggar, 2010). Therefore, as predation is known to be the main causes of M in wild fish stocks, the high estimate of M for O. niloticus and conversely, lowest M for C. gariepinus is thus expected. C. carpio as fast growing fish also presents a high M value in Lake Koka and our estimate is comparable to the findings of other authors (Winker et al., 2011).
We estimated Z from length converted catch-curves but did not include for the analysis those large specimens, whose lengths are close to L o following the reasoning of Pauly (1984), Hicks & McClanahan (2012) and Gay-anilo et al. (2005). According to them their inclusion would generate unrealistically high ages and low Z estimates. Moreover, the catch curve for C. gariepinus does not seem to fit well with its inherent assumption of constant Z for sizes beyond Lc. The slope of the curve drastically drops toward the larger/older fish (age > 11 years) suggesting that those fish sizes are significantly less affected by the fishing gear. However, these larger fish correspond to the group of Mega-spawners as their size is above 10 % of L opt. They comprise < 5 % of the catch and are assumed to mostly suffer from natural mortality causes. We thus, choose only those data points that correspond to the other 95 % of the catch and that provided a linear fit to the catch curve and calculated the corresponding Z value, which was then used for our subsequent analysis. For C. gariepinus and O. niloticus, the exploitation rate (E) resulted slightly above or below the 0.5 (depending on the M -value used), a rate considered as optimum level of exploitation (E opt) (Gulland, 1971), while it was consistently significantly below the 0.5 value for C. carpio.
When we look at the size indicators for the state of the fishery, the catch size distribution showed that more than two-thirds of the C. gariepinus catch lies below the size of L m and only 28 % of the catch lies within the L opt range suggesting that growth overfishing is occurring and the very low percentage of mega-spawners would also suggests recruitment overfishing, which is in agreement with the exploitation rate estimate based on Pauly's M estimate. However, although the percentage of mega-spawners in the stock is low, recruitment overfishing for C. gariepinus in Lake Koka is unlikely to occur as the catch curve clearly showed low fishing pressure on the mega-spawners. Hence, large specimens are rarely caught and their percentage has remained nearly constant over the years, which would agree with the exploitation rate estimate based on Rikhter and Evanov's formula to estimate M. The possible explanation of a lower F value for the larger sizes could be related to the fishing ground and fishing gears used in Lake Koka. The Beach seine, which contributes about 60 % of the catch annually, is commonly deployed in the littoral zone (an area close to the shoreline of the lake), where juveniles and young adult fish forage and are principally found, whereas large adults prefer deeper areas. Ontogenetic habitat shifts are well known in most exploited fish stocks. A study on the bathospatial distribution of fishes in Lake Victoria showed that, while specimens of C. gariepinus were found in all depths ranging from 0 to 80 m (Kudhongania & Cordone, 1974; Witte & de Winter, 1995), adult fishes were found to prefer deepwater while the juveniles stay mainly in littoral areas (Goudswaard & Witte, 1997). A similar study in Lake Tana revealed that juveniles and smaller C. gariepinus were confined to the vegetated littoral zone while larger adults were found mainly in deeper areas (Wudneh, 1998). Furthermore, many studies also suggested the existence of ontogenetic migration between different habitats (e.g. from sea grass beds to deep reefs or from littoral to open/pelagic and deeper areas) during their life cycle and different habitats or landscapes could result in different fish assemblages (Dorenbosch, Grol, Nagelkerken, & Velde, 2006; Kimirei, Nagelkerken, Griffioen, Wagner, & Mgaya, 2011; Hicks & McClana-han, 2012). The other two gears (gillnets & longline) used in Lake Koka could be used in deeper areas and can catch larger specimens if large mesh and hook sizes were used. However, their commonly used mesh and hook sizes also select against very large sizes unlike the beach seine, which selects all sizes classes beyond Lc along the seining area. We, therefore conclude that growth overfishing is the main problem of C. gariepinus stock in Lake Koka.
The E - value computed for C. carpio is the lowest (<0.5) compared to the other species with both M values considered, indicating that the C. carpio stock in Lake Koka is underex-ploited. However, similar to C. gariepinus, the catch size distribution showed that only 50 % of the catch falls above the L m and only 43 % lies within the L opt range suggesting that growth overfishing may be occurring. The percentage of mega-spawners showed an increasing trend and arrives at levels > 10 % as of 2010, which suggests no recruitment overfishing, which is in agreement with the estimates for the exploitation rate. In addition, C. carpio like C. gariepinus is a bottom dweller and hence, the larger adults seem not to be much affected by the fishery with the same explanation given above for C. gariepinus. In fact, according to the index proposed by the American Fisheries Society (AFS), the estimated K values and its fecundity suggests that C. carpio is a highly resilient and productive fish (http://www.fish- base.org/download/keyfacts.zip "Accessed 20 August 2014").
Although the Z value for O. niloticus is higher than for the other two species, E computed using both M values is near 0.5, suggesting no overfishing. The catch size composition also showed that more than 80 % of the catch comprises sizes above L m and about 50 % lies in the L opt range and mega-spawners comprise more than 20 %, suggesting both recruitment and growth overfishing are not occurring. The similarity of Lc and L opt values also indicates that the O. niloticus fishery in Lake Koka is healthy. We also evaluated the possible changes of E for all the species using the values of Lx and K within their 95 % CI and found slight change in the mortality parameters and E values, which, however, do not affect the overall conclusion on exploitation status for all the three species.
The fish production potential estimated for Lake Koka using empirical models (1 360 t/ year by Tesfaye and Wolff (2014) and 1 500 t/ year by LFDP (1994)) is far beyond the current production level of about 625 t, suggesting that there is a room for production expansion.
Our study indeed suggests that fishery production may be increased by increasing the exploitation rate on the underexploited C. carpio and possibly by increasing the size at first capture of all the three species. This would reduce the numbers caught below L m and would increase the numbers of fish caught in the L opt range. Froese, Stern-Pirlot, Winker and Gascuel (2008) demonstrated that fishing within the L opt range maximizes yield and spawning biomass and would be a step towards a sustainable ecosystem-based fisheries management. It might also be possible to increase production by expanding the fishing grounds of C. carpio and C. gariepinus towards the deeper parts of the lake after careful assessment of the economic and ecological feasibility of offshore and demersal fishing grounds, which seem presently to serve as a natural reserve to replenish the stocks.












 uBio
uBio 



