Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO  uBio
uBio
Share
Revista de Biología Tropical
On-line version ISSN 0034-7744Print version ISSN 0034-7744
Rev. biol. trop vol.57 suppl.1 San José Nov. 2009
Human population structure of the Costa Rican Central Provinces. An evaluation through isonymic methods
Andrés E. Sáenz & Ramiro Barrantes
Escuela de Biología Universidad de Costa Rica, 11501-2060, San José, Costa Rica; andres.saenz@ucr.ac.cr; rabar@cariari.ucr.ac.cr
Abstract: The human population structure of the Central Provinces of Costa Rica was analyzed through isonymic methods and the use of Electoral Registers (1990 and 2006). Four parameters that define, in a genetic and evolutionary context, this structure were estimated: the consanguinity due to random mating (Mortons a-priori kinship Fii), the genetic isolation (Fishers α), the migration (Karlin-McGregors υ), and the degree of subdivision or population differentiation (Fst). The possible geographical distribution of these variables is shown by the use of a Principal Components Analysis (PCA). There is a coincidence between groups of counties obtained by similarity in surname diversity and their geographic location in the territory. Differences were found for the values of the components of consanguinity (F=15.6; p<0.05) and genetic isolation (F=14.38; p<0.05) between different sectors of the Central Provinces. There is an association between population density and the breaking up of genetic isolates and another possible association between the geography of the region, the migration patterns of individuals, and the consequent levels of inbreeding and genetic isolation. The differences in the values of population structure components, inbreeding and genetic isolation, between the different zones of the central region, allow the assumption of the existence of differences in gene frequencies. The migration of blocks of genes from the center to the periphery is also possible and the variation in this sense might be attributed mostly to changes in the components of the population structure: mating patterns, migration and the consequence of the effective population size in the genetic drift process. Rev. Biol. Trop. 57 (Suppl. 1): 371-379. Epub 2009 November 30.
Key words: population structure, isonymy, inbreeding, genetic isolation, migration, PCA, Costa Rica.
The population structure refers fundamentally, from a genetic and population perspective, to the way matings are distributed, the movement of individuals or groups and the effect and fluctuation of the effective population size (Cavalli-Sforza & Bodmer 1971). The nonrandom character of unions leads to the establishment of groups with different levels of reproductive separation and isolation inside wider populations, and their distribution results in the geographic division of the territory and, therefore, the behavior of individuals in terms of migration and reproduction. This partial fragmentation of human populations has important consequences for the distribution of the genetic variability and constitutes an important foundation in many areas of basic and applied human genetics.
In Costa Rica several studies about the population structure have been conducted, relying mainly in the consanguinity, estimated through the inbreeding coefficient (F), the migration and the regional and temporal variation (Barrantes 1978, Zumbado & Barrantes 1991), and more precisely in the Central Valley (Zumbado & Barrantes 1991, Madrigal & Ware 1997, Morera & Barrantes 2004). On the other hand, several investigations consider the Central Valley an appropriate site for the study of complex diseases and support this reasoning in the populations colonial history and a hypothetical genetic homogeneity (Freimer etal. 1996, McInnes et al. 1996, Morera & Barrantes 2004); even though an analysis of its population structure is not stated by the authors in the previous mentioned terms.
Crow & Mange (1965) were the first to develop a formal method to estimate inbreeding levels in human populations through the proportion of isonymous unions. The use of this method has been applied to different localities around the world as a form of inferring population structure. Since then, the method has also been adapted for the use of frequency distributions of surnames to estimate various components of the population structure, including inbreeding, migration, drift and isolation (Zei et al. 1983, Pinto- Cisternas et al. 1985, http://www.consang.net for a general review).
Two main objectives of the present study are: first, to analyze various components of the population structure of the Central Provinces of Costa Rica for two periods, through the use of appropriate isonymy methods and models for their estimation. Second, to evaluate the geographic and temporal variations of these components and their effect on the population subdivision process.
Materials and methods
The Costa Rican territory is divided in seven Provinces. These Provinces are then subdivided in Counties and each County is again subdivided in smaller regions called Districts. The Central region is spanned by Counties belonging to four different Provinces. These provinces are San José, Alajuela, Heredia and Cartago and the number of Counties that are located in the Central territory, chosen for this study, include the Central Valley in addition to four more Counties south of San José and one County of Cartago (Table 1).
Two electoral registers were collected from two different sources. The 2006 electoral register was obtained from the governments Tribunal Supremo de Elecciones (http:// www.tse.go.cr/), and the 1990 electoral register came from the Centro Centroamericano de Población (CCP) of the University of Costa Rica. Both electoral registers were stored in Access (Microsoft) software for database storage and management. Microsoft Excell (Microsoft) software was used for analyzing the data. The 2006 electoral register consisted of a sample of 2.608.234 individuals from the whole country. The 1990 electoral register consists of a sample of 1.692.050 individuals from the whole country. The electoral population grew in almost a million persons in 16 years. The electoral register possesses the advantage of not being biased by socioeconomic status and constitutes a large sample of the population, it is in fact, the whole population of Costa Rican nationality, above 18 and alive, in the country, at the year the register was made. The electoral register was filtered to obtain data from single Counties. The same methodology employed as in Barrai et al. (1996) was followed, but because the analysis is for a Latin American population, it was carried out on both surnames. Using the 2006 and the 1990 electoral registers and for each County of the Central Provinces, the following parameters were calculated: a) the unbiased random isonymy (Iii), a value related to surname diversity; b) Fishers α value, is an estimate from Fishers (1943) logarithmic distribution that was developed to measure species diversity in a random sample of animal population and it is used here to estimate surname diversity and infer genetic isolation. According to Rodríguez-Larralde et al. (1993):
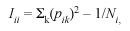
where pik is the relative frequency of surname k in he ith County, and Ni is the sample size of the same County which, in this study, is the number of electors multiplied by a factor of two, because each individual contributes with two surnames. Fishers (Fisher 1943) α was directly estimated from:
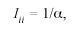
as derived by Barrai et al. (1992).
c)The consanguinity due to random mating in population i, Φii, was calculated according to Rodríguez Larralde et al. (1993):
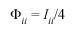
Φii is the equivalent of the Mortons withingroup a-priori kinship (Morton 1973) and estimates inbreeding. In this paper Fst is used, and its value is equivalent to Fr. Karlin-McGregors (1967) , an indicator of migration rate was estimated as:
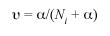
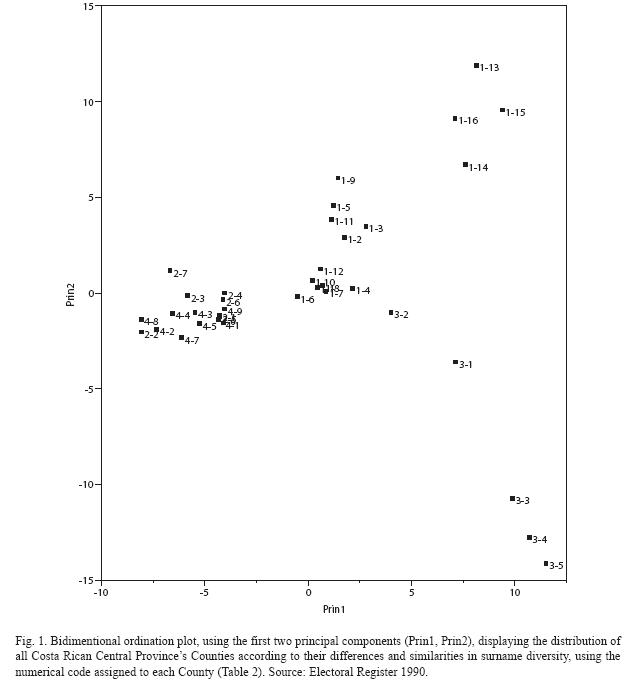
from the formula given by Zei et al. (1983). A Principal Component Analysis (PCA) (Bryan 2005) on the distribution of the 95 most frequent surnames from the Counties of the Central Provinces from the 1990 electoral register data is also presented. The relative frequencies of surnames were used in order to avoid a bias from comparing absolute frequencies among Counties with large differences in sample sizes. A bidimentional plot using the first two principal components relates the different Counties of the region in regard to surname distribution similarity. In this way a graphic representation of the actual Central regions population structure is obtained (Fig. 1).
Non parametric ANOVAs (Kruskal & Wallis 1952), with Bonferroni test for adjustment of the significance value, were carried out for both principal components between different groups of Counties to assess the statistical significance of their distances in the ordination plot. Two one way ANOVAs were used to compare the means of the α estimate and the Φii estimate between these same groups of Counties. Dunns post hoc test (Dunn 1964) for non parametric ANOVA and Tukey-Kramer post hoc test (Kramer 1956) for one way ANOVA were used to make multiple mean comparisons.
Results
Principal Components and regionalanalysis: In the Central region of the country, 4 distinct groups can be visualized according to their differences in surname diversity (Fig. 1). The first two principal components used to construct this ordination plot explain 23% of the variance from the surname distribution data. The Counties of Alajuela and Heredia Provinces cluster together while the San José
Province Central Counties form a group located in the center of the graphic. The third group atthe right and lower part of the figure is formed by Counties belonging to Cartago Province. The fourth group, consisting of four Counties from the South part of San José Province (Dota, Tarrazú, León Cortés and Acosta) collectively named, Los Santos, is very isolated from the other group of this same Province and can be located in the top right corner of the diagram. Significant differences were found between Alajuela-Heredia group and all other groups, but no significant differences between the remaining three groups for the first principal component which explains 12.5% of the variance (x2=31.4, df=3, p<0.025). The second principal component explains 10% of the variance and showed no significant difference between both groups from San José Province; nor between the Cartago and Alajuela-Heredia groups; but both pairs of groups did show significant differences between them (x2=28.3, df=3, p<0.025).
There was no significant change from the principal component analysis with the 2006 sample data compared to that of the 1990 data presented here. The four groups and their respective Counties remained very closely the same throughout this 16 year period. The results for the ANOVA test of principal components were also similar for both data series.
Fishers α and Genetic Isolation: A comparison was made of Fishers α mean measurements between the four groups of Counties identified by the principal components analysis. Significant differences were obtained only for the group from the Central Counties of SanJosé Province (F=14.38, df=3, p<0.05).
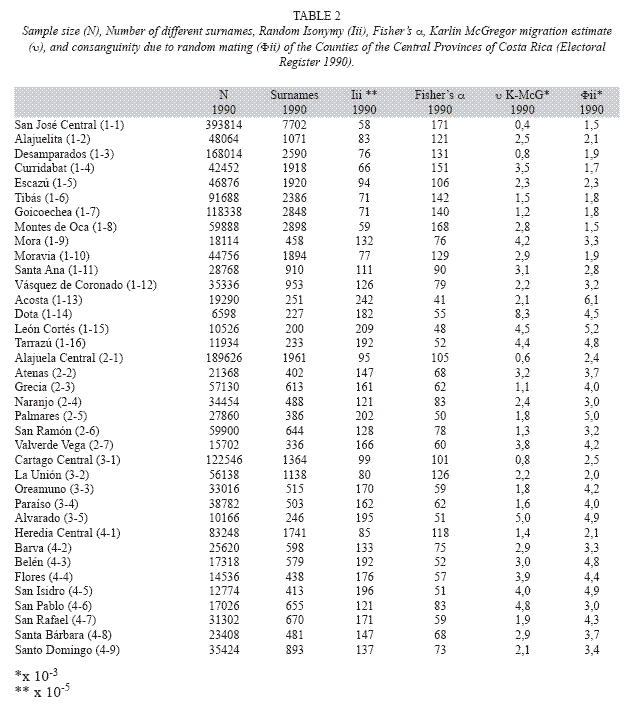
In terms of surname diversity, the most diverse Counties, with α values in the range 100 to 171, correspond to nearly all of the Central Counties of San José Province (San José Central, Alajuelita, Desamparados, Curridabat, Escazú, Tibás, Goicoechea Montes de Oca and Moravia); the head Counties of the other four Provinces (Alajuela Central, Heredia Central, Cartago Central) and one County of Cartago Province (La Unión). In the intermediate range of 60<α<100 Counties from Alajuela and Heredia Provinces are abundant (Atenas, Grecia, Naranjo, San Ramón, Valverde Vega, Barva, San Pablo, Santa Bárbara, Santo Domingo) but also three Counties from San José Province (Mora, Santa Ana, Vásquez de Coronado) and one from the Province of Cartago (Paraíso) can be found. In the lowest range of surname diversity 41<α<60 four Counties of San José Province known as Los Santos (Acosta, Dota, León Cortés, Tarrazú), four Counties from Alajuela and Heredia Provinces (Palmares, Belén, Flores, San Isidro) and two Counties from Cartago Province (Oreamuno and Alvarado) can be observed (Table 2).
Since 1990, the αvalues have been relatively unchanged. There are a few exceptions in San José, regarding Santa Ana, Escazú and Vásquez de Coronado with higher α scores for the 2006 sample. There is also an augmentation of the α value for all the Counties of Heredia but this pattern is quite remarkably uniform for the Province so that the relative isolation of the different Counties between them is maintained over time.
Consanguinity: The same analysis made for α was carried out for the Φii estimate. This variable followed normal distribution (Shapiro- Wilk W= 0.95; p>0.05) and variances among different treatments were homogeneous (Bartlett F= 1.01; p>0.05). Significant differences were found among groups except for the Alajuela-Heredia group and the Cartago group (AdjR2= 0.55; F ratio= 15.6; df= 3; p<0.05). Both San Josés Central Counties group and Los Santos group had the lowest and highest averages respectively while Alajuela-Heredia and Cartago groups had intermediate values for Φii.
The groups of Counties classified by low (1.5<Φii<2.5); intermediate (2.5<Φii<4.0), and high (4.0<Φii<6.1) levels of inbreeding are the same groups classified as having high, intermediate and low levels of surname diversity (see results for Fishers α), respectively (Table 2). The statistical differences between groups of the Central Provinces for Fishers and the coefficient of inbreeding Φii gave the same results with the 2006 data.
Migration: The Karlin-McGregor υ migration estimate for the 1990 surname data gave conflicting results. So, for certain isolated Counties like Acosta, with low αvalues (41), the migration estimate υ was also low (2.1); but for a County like Dota, with similar α value (55) and close relationship in terms of surname distribution (Fig. 1) the immigration was estimated to be four times larger (υ=8.3). On the other hand, Counties within large urban regions, such as San José Central and Desamparados gave very low migration estimates: υ=0.4 and υ=0.8 respectively, while other Counties of comparable urban development, like Curridabat, gave higher but still relatively low migration rates (υ=3.5) (Table 2). When compared with the 2006 surname data, Karlin- McGregors υ migration estimate gave the same tendency for all Counties which is a slight decline in its value, thus a lower immigration rate for the more recent period.
Discussion
The four main groups identified by their similarities in surname diversity revealed a striking coincidence with geographic location: The Counties of Alajuela and Heredia in the western part of the Central Valley, San Josés Counties at the Center, Cartagos Counties in the eastern part of the Valley and the four Counties of San José known as Los Santos (Acosta, León Cortés, Tarrazú and Dota) geographically
located next to each other south of the Province. This indicates that the genetic isolation and differentiation between the regions of the Central Provinces of the country are related to the geography and seem to adjust to an "isolation by distance" model (Wright 1943). Indeed, locations geographically closer exhibit higher similarity in terms of surname diversity and inbreeding (Fig. 1, Table 2). There should however be caution when interpreting these results given the low (23%) percentage of variance in surname distribution explained by the principal components test.
In terms of inbreeding, it can be observed that certain regions have higher or lower levels of consanguinity and depending on the region the inbreeding levels will vary with statistical significance. The zone of Los Santos and the Central Counties of San José stand out for being the most and less inbred (Φii) regions of the Central Provinces respectively. These same results were observed in previous studies (Zumbado & Barrantes 1991).
There are differences in the isolation (α) values obtained for the different sectors of the Central Provinces and these differences are also statistically significant. In the range of high α values nearly all of the Central Counties of San José Province can be found. This zone corresponds also to the most densely populated region of the Central Provinces. Thus, we can observe an association between the population density and the breaking of isolates for this territory. There is also a possible association between the geography of the region, and thus the behavior of individuals in terms of migration, and the resulting values of inbreeding and surname diversity levels.
Karlin-McGregor υ was found to be a conflicting estimate of migration rates. The results in this study seem to be a product of this estimates sensitivity to sample size (N), so that highly populated Counties gave very low immigration rates and vice versa. Also the general pattern of slight decline of the immigration rate for the 2006 period (data not shown) seems to reflect a change of demographic growth more than anything else, after the electoral population grew in almost a million persons in 16 years. This same issue has been addressed in other isonymy studies that employed this estimate (Barrai et al. 1996). This particular issue does not affect Fishers α, which estimates isolation and drift whatever the N value, and is thus independent of sample size (Zei et al. 1983, Barrai et al. 1996). Nonetheless, smaller localities tend to be more inbred and have less surname diversity than wider areas, thus, α is expected to show a certain behavior as a function of the size of the local populations.
The population structure of the Central Provinces of Costa Rica, analyzed through several isonymic methods, shows differences in the components of inbreeding and isolation for different regions. This allows the assumption that differences in gene frequencies might exist between different sectors of this territory. A migration of blocks of genes from the center to the periphery is also probable. The variation in this sense could be attributed mostly to changes in the population structure components: mating patterns, migration and the consequence of the effective population size on the genetic drift process.
Aknowledgments
The authors would like to thank Claudio Alpízar and Héctor Fernández from the Tribunal Supremo de Elecciones for providing the 2006 electoral register, and Roger Bonilla of the CCP (University of Costa Rica) for making the 1990 electoral register available to us. This investigation was supported with funds from the University of Costa Rica (Grant Nº 111-A6-047).
Resumen
Se analiza la estructura de varias poblaciones humanas de las provincias centrales de Costa Rica mediante métodos isonímicos y utilizando los Padrones Electorales (1990 y 2006). Se estimaron cuatro parámetros que definen, en un contexto genético y evolutivo, esta estructura: la consanguinidad por cruces aleatorios (a-priori Kinship de Morton Φii), el aislamiento genético (α Fisher), la migración (υKarlin-McGregor) y el grado de subdivisión o diferenciación de las poblaciones (Fst). La posible distribución geográfica de estas variables se muestra utilizando un análisis de componentes principales. Existe una coincidencia entre grupos de cantones obtenidos por similitud en diversidad de apellidos y la localización geográfica de los mismos en el territorio. Se encontraron diferencias estadísticamente significativas en los valores obtenidos para los componentes de consanguinidad (F=15.6; p<0.05) y aislamiento genético (F=14.38; p<0.05) entre diferentes sectores de las provincias centrales. Existe una asociación entre la densidad poblacional y la quiebra de aislados genéticos y otra posible asociación entre la geografía de la región y los patrones de migración de individuos y los consecuentes niveles de endocruzamiento y aislamiento genético. Las diferencias en los valores de los componentes de consanguinidad y aislamiento entre diferentes zonas del territorio central permiten suponer la existencia de diferencias en frecuencias génicas. La migración de bloques de genes del centro a la periferia también es posible y la variación en este sentido podría atribuirse principalmente a cambios en los componentes de la estructura poblacional: patrones de cruces, migración y la consecuencia del tamaño efectivo de población en procesos de deriva genética.
Palabras clave: estructura de la población, isonimia, consanguinidad, aislamiento genético, migración, PCA, Costa Rica.
Received 03-X-2007. Corrected 30-VIII-2009. Accepted 04-X-2009.
References
Barrai, I., G. Formica, C. Scapoli, M. Beretta, S. Volinia, R. Barale, P. Ambrosino & F. Fontana. 1992. Microevolution in Ferrara: isonymy 1890-1990. Ann. Hum. Biol. 19: 371-385. [ Links ]
Barrai, I., C. Scapoli, M. Beretta, C. Nesti, E. Mamolini & A. Rodríguez-Larralde. 1996. Isonymy and the genetic structure of Switzerland: The distributions of surnames. Ann. Hum. Biol. 23: 431-455. [ Links ]
Barrantes, R. 1978. Estructura poblacional y consanguinidad n Dota. Costa Rica. 1888-1962. Rev. Biol. Trop. 26: 347-357. [ Links ]
Bryan, F.J. Manly. 2005. Multivariate statistical methods: primer. Chapman & Hall/CRC. USA. [ Links ]
Cavalli-Sforza, L.L. & W. Bodmer. 1971. Human Population Genetics. Freeman, San Francisco, USA. [ Links ]
Crow, J.F. & A.P. Mange. 1965. Measurements of inbreeding from the frequency of marriages between persons of the same surnames. Eugen. Quart. 12: 199-203. [ Links ]
Dunn, O.J. 1964. Multiple contrasts using rank sums. Technometrics 6: 241-252. [ Links ]
Fisher, R.A. 1943. The relation between the number of species and the number of individuals in a random sample of animal population. J. Anim. Ecol. 12: 42-58. [ Links ]
Freimer, N.B., V.I. Reus, M.A. Escamilla, M. Spesny, L. Smith, S. Service, A. Gallegos, L. Meza, S. Batki, S. Vinogradov, P. Leon & L.A. Sandkuijl. 1996. An Approach to investigating linkage for bipolar disorder using large Costa Rican pedigrees. Am. J. Med. Genet. 67: 254-263. [ Links ]
Karlin, S. & J. McGregor. 1967. The number of mutant forms maintained in a population. Proc. Fifth Berkley Symp. Math. Stat. Prob. 4: 415-438. [ Links ]
Kramer, C.Y. 1956. Extension of multiple range tests to group means with unequal numbers of replications. Biometrics 12: 307-310. [ Links ]
Kruskal, W.H. & W.A. Wallis. 1952. Use of ranks in onecriterion analysis of variance. J. Amer. Statist. Assoc.
47: 583-621.
Madrigal, L. & B. Ware. 1997. Inbreeding in Escazu, Costa Rica (1800-1840, 1850-1899): isonymy and ecclesiastical dispensations. Hum. Biol. 69: 703-714. [ Links ]
McInnes, L.A., M.A. Escamilla, S.K. Service, V.I. Reus, P. Leon, S. Silva, E. Rojas, M. Spesny, S. Baharloo, K. Blankenship, A. Peterson, D. Tyler, N. Shimayoshi, C. Tobey, S. Batki, S. Vinogradov, L. Meza, A. Gallegos, E. Fournier, L.B. Smith, S.H. Barondes, L.A. Sandkuijl & N.B. Freimer. 1996. A complete genome screen for genes predisposing to severe bipolar disorder in two Costa Rican pedigrees. Proc. Natl. Acad. Sci. USA 93: 13060-13065. [ Links ]
Morera, B. & R. Barrantes. 2004. Is the Central Valley of Costa Rica a genetic isolate? Rev. Biol. Trop. 52: 629-644. [ Links ]
Morton, N.E. 1973. Kinship and population structure, p. 66-71. In N.E. Morton (ed.). Genetic structure of populations. University Press of Hawaii. Honolulu, Hawaii, USA. [ Links ]
Pinto-Cisternas, J., M. C. Castelli & L. Pineda. 1985. Use of surnames in the study of population structure. Hum. Biol. 57: 353-363. [ Links ]
Rodríguez-Larralde, A., I. Barrai & J.C. Alfonzo. 1993. Isonymy structure of four Venezuelan States. Ann. Hum. Biol. 20: 131-145. [ Links ]
Wright, S. 1943. Isolation by distance. Genetics 28: 114-138. [ Links ]
Zei, G., R. Guglielmino Matessi, E. Siri, A. Moroni & L. Cavalli-Sforza. 1983. Surnames in Sardinia: Fit of frequency distributions for neutral alleles and genetic population structure. Ann. Hum. Genet. 47: 329-352. [ Links ]
Zumbado, A.L. & R. Barrantes. 1991. Consanguinidad en las provincias centrales de Costa Rica. Acta Med. Cost. 34: 75-82. [ Links ]
Internet references
Tribunal Supremo de Elecciones. 2007. Tribunal Supremo de Elecciones República de Costa Rica. (Downloaded: 03/2007, http://www.tse.go.cr/). [ Links ] Bittles, A. 2001. Consanguinity endogamy resource. Edith Cowan University, Murdoch University & Center for comparative genomics. Australia (Downloaded: 09/2007, http://www.consang.net/) [ Links ]