Introducción
Como parte de su quehacer, la carrera de Bachillerato y Licenciatura en la enseñanza de la Matemáticas (BLEM) de la Universidad Nacional (UNA) busca formar profesionales competentes con conocimientos de las nuevas tendencias en educación matemática y, de esta manera, brindar un aporte a la educación costarricense. Por ello, desde el año 2017, transforma su antiguo plan de estudios centrado en contenidos a uno basado en competencias. Estos esfuerzos de mejora continua de la Escuela de Matemática se centran en reducir los índices de reprobación mediante estrategias pedagógicas como mejorar la secuencia de los cursos y realizar cambios en la evaluación, dejando de centrarla en exámenes e incorporando otros rubros como proyectos, portafolios, exposiciones, trabajos en equipo, etcétera (Universidad Nacional, 2017).
Sin embargo, a pesar de los cambios, el bajo rendimiento académico en matemáticas (RAM) sigue sien- do una problemática, tal y como lo demuestra el sistema de Estadísticas Estudiantiles de la UNA (EEUNA, 2019); en el cual se puede constatar que el curso de Matemática Fundamental, primera asignatura del área de Matemática del BLEM, es uno de los cursos de más bajo rendimiento académico en la UNA, con un promedio de 5,60 (escala de 0-10). Además, considerando todos los cursos del BLEM, se tiene un pro- medio de 6,87 (cohortes 2017 y 2018).
Asimismo, diversos estudios señalan que estudiantes de la carrera BLEM muestran altos niveles de reprobación y deserción, bajo RAM y deficiencias académicas (Calderón, 2014; Chaves, 2003; Zamora- Araya y Villalobos-Madrigal, 2018a, 2018b). Más aún, Pascua-Cantero (2016) y Zamora-Araya y Villalobos- Madrigal (2018b) indican que algunos estudiantes expresan que la carrera no es lo que pensaban, la mayoría de los casos por la dificultad y las expectativas de los cursos de matemática. Adicionalmente, los estudiantes que eligen la carrera BLEM en su mayoría lo hacen por la creencia en sus buenas capacidades en matemáticas adquiridas en la educación secundaria (Calderón, 2014).
Por esta razón, el rendimiento académico cobra relevancia para el BLEM por ser uno de los indicado- res de calidad utilizado para explicar el éxito y el fracaso en el proceso de enseñanza y aprendizaje (Garbanzo Vargas, 2013; Lamas, 2015). Asimismo, el rendimiento académico es un concepto multidimensional y complejo, que por lo general se define como un método para medir logros, conocimientos, habilidades y competencias adquiridos por el estudiantado en el proceso de enseñanza y aprendizaje; expresado habitualmente por calificaciones concedidas por profesores bajo el supuesto de una valoración ecuánime (Urquijo, 2002; Martínez Padrón, 2008; Erazo-Santander, 2011).
Por este motivo, se deben considerar diversos factores a la hora de estudiar el rendimiento académico entre ellas: motivación, autoeficacia, estados emocionales, cantidad de cursos matriculados, cursos reprobados, nivel de carrera, creencias, género, autoconcepto, nivel educativo de los padres, contexto educativo, entre otros; de manera que se pone de manifiesto un conjunto de actitudes y conductas que pueden resultar beneficiosos o desventajosos para rendimiento académico (Bandura, 1993, 1999; Calderón, 2014; Barahona, 2014; González-Pienda, 2003; Edel, 2003; Carrillo Regalado y Ríos Almodóvar,2013; Chong, 2017).
De entre todos estos factores, la investigación se enfocará en estudiar el concepto de autoeficacia matemática, enmarcada en la teoría social cognitiva de Bandura (1993) y su influencia en el RAM de las personas estudiantes matriculadas en el nuevo programa de estudio del BLEM. Por tanto, el principal objetivo es el de analizar, mediante un análisis de regresión múltiple, la relación entre la autoeficacia matemática y el RAM en estudiantes del BLEM en la UNA; utilizando como variables de control: sexo, tenencia de beca, nivel educativo de los padres, elección de carrera, nivel de carrera y condición de reprobación.
Adicionalmente, se establecen como objetivos específicos: (1) determinar el peso relativo que tiene cada una de las dimensiones de la autoeficacia matemática con el RAM, así como (2) mostrar la importancia de las demás covariables a la hora de explicar el RAM en estudiantes del BLEM.
Con ello, se pretende evidenciar el grado de relación que guardan cada una de las fuentes del constructo de autoeficacia (experiencia directa, experiencia vicaria, persuasión social y factores fisiológicos) y las otras variables consideradas con el RAM.
En cuanto a la dirección de las relaciones bivariadas, se asume que existe una relación positiva entre el RAM y las covariables de elección del BLEM como primera opción, tenencia de beca, el nivel de estudios de la madre y el nivel de la carrera (Bourdieu, 2015; Bourdieu y Passeron, 1977; Zamora-Araya, 2020); así como una relación inversa con la reprobación en cursos de alto contenido matemático (Díaz, Cruz y Carrillo, 2018, Fernández et al., 2017).
Marco teórico
Teoría social cognoscitiva
El fundamento que enmarca la teoría social cognoscitiva es la idea de que el aprendizaje se obtiene de procesos cognitivos y la dependencia con el entorno social en el que se desarrolla (Bandura, 1991, 1993). De este modo, el aprendizaje al ser llevado a cabo en un ambiente social permite a las personas aprender mediante la observación de modelos y de conductas de los demás y, a partir de ello, operan por las creencias que tienen respecto de sus propias habilidades y acorde con los resultados anhelados de sus acciones que les permite adquirir conocimientos, habilidades, estrategias, creencias y actitudes (Bandura, 1977,1982).
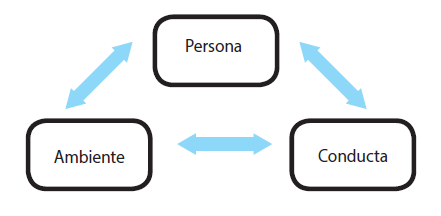
Asimismo, faculta para explicar la complejidad de los procesos epistemológicos de los seres humanos en el momento de ejecutar una determinada conducta, Bandura (1994, 1999) analiza el proceso median- te un esquema de reciprocidad triádica (figura 1) entre la conducta, el ambiente y los factores personales que operan como determinantes que interactúan e influyen de forma bidireccional.
Por otra parte, la autoeficacia percibida (factor personal) es un constructo fundamental en el esquema de reciprocidad triádica como mecanismo autorregulador del aprendizaje, pues las creencias y perspectivas sobre las propias capacidades del individuo influyen en el logro y en la elección de conductas, asimismo, la influencia del entorno puede modificar esas creencias mediante la persuasión social y/o la observación de modelos (Bandura, 2001; Zimmerman, 1989). Por tanto, muchos estudios han utilizado la teoría social cognoscitiva para relacionar o explicar el rendimiento académico de los estudiantes (persona), puesto que el aprendizaje se desarrolla dentro de un entorno académico (ambiente), en donde el individuo desempeña diferentes tareas (conducta); en particular, la autoeficacia percibida como predictor en el rendimiento académico (Galleguillos Herrera y Olmedo Moreno, 2017; Honicke y Broadbent, 2016; W. Lee, Lee y Bong, 2014).
Autoeficacia matemática
Las expectativas de las personas acerca de su autoeficacia son específicas del entorno social y del cumplimiento de determinadas conductas (Pajares, 1996). Por consiguiente, adquiere sentido definir el constructo de autoeficacia matemática para referirse a una evaluación específica de juicios, perspectivas y creencias sobre la confianza de un individuo en su capacidad para ejecutar con éxito una tarea o problema matemático (Hackett y Betz, 1989).
Sin embargo, la creencia de los individuos sobre su eficacia personal es consecuencia de cuatro fuentes de interacción que, según Bandura (1977, 1982), ejercen influencia sobre la conducta del individuo.
Experiencia directa: fuente que ejerce mayor influencia en la autoeficacia, ya que se basa en las propias experiencias del individuo, relacionada con los éxitos y fracasos en el cumplimiento y ejecución de tareas. En este sentido, los logros aumentan las expectativas de eficacia y las fallas repetidas las disminuyen.
Experiencia vicaria: las personas evalúan su eficacia al observar a los demás realizando determina- das conductas, y a partir del éxito o fracaso de lo observado el espectador diagnostica su autoeficacia. No obstante, las expectativas de eficacia inducidas por el modelado son endebles al cambio en comparación con la experiencia directa.
Persuasión verbal: es la influencia tanto positiva como negativa en frases u opiniones de otras personas sobre la eficacia propia del individuo. No obstante, estas expectativas de eficacia inducidas por profesores, compañeros o amigos son en general más débiles que las derivadas de los propios logros, dado que no suministran una base experiencial auténtica para el individuo.
Factores fisiológicos: al efectuar una determinada labor académica se presentan situaciones estresantes y exigentes que provocan una excitación emocional que repercute en la competencia del sujeto. Se destacan, estrés, ansiedad, estados de ánimo, miedos, fatiga, entre otros.
De esta manera, diferentes estudios han mostrado que la autoeficacia es un predictor en el rendimiento académico, en diferentes niveles, prescolar, primaria, secundaria y universitario en grado y posgrado (Alpuche Hernández y Vega Pérez, 2014; Del Rosal y Bermejo, 2018; Portilla Vargas, 2018; Oriol-Granado, Mendoza-Lira, Covarrubias-Apablaza y Molina-López, 2017). En el caso de la educación terciaria, se han realizado estudios sobre las creencias cognoscitiva en estudiantes de ingeniería, psicología, medicina, pedagogía, educación física, entre otras (Martínez y Medina, 2019; Turgut, 2013; Rivera, Llanes, Garrido, Maldonado y Sánchez, 2014).
Por ello, el presente documento pretende contribuir, en la misma línea, con un estudio que muestre la relación de la autoeficacia con el rendimiento académico en un contexto matemático, razón por la cual se consideran únicamente los cursos del BLEM directamente relacionados con esta disciplina.
Metodología
Diseño de la investigación
Según Villalobos (2017), la investigación es no experimental, de corte transversal y de diseño correlacional; puesto que los datos se recolectaron en un solo momento, con el objetivo de conocer el grado de asociación entre las variables sin su manipulación. Para tal fin, se aplicó un cuestionario autoadministra- do, descrito en las siguientes secciones.
Participantes
Las personas participantes del estudio son estudiantes de primero, segundo y tercer nivel del grado de bachillerato, pertenecientes al plan de estudio de la carrera BLEM implementado en el 2017 en la UNA, sede Omar Dengo. La recolección de la información se llevó a cabo durante el II Ciclo del 2019 y los criterios de inclusión fueron: (a) asistencia durante la aplicación del cuestionario, (b) firmar el consentimiento para participar en el estudio, en el cual se garantizaba la anonimidad de la persona participante y (c) que la persona estudiante se encontrara matriculada en al menos un curso de alto contenido matemático; los cursos se identifican en la malla curricular del BLEM por iniciar con las siglas MAC, los cuales pertenencen a las áreas disciplinares de Matemática Formal, Matemática Aplicada y Estadística.
Métodos de trabajo y descripción del instrumento
Se obtuvo la autorización de la Escuela de Matemática de la UNA, mediante el coordinador de carrera y el profesorado encargado de los cursos, para aplicar el instrumento al estudiantado. Las personas que accedieron a completar el cuestionario firmaron un consentimiento informado donde autorizaron el uso de los datos para fines investigativos.
Los investigadores aplicaron el cuestionario en todos los grupos con código MAC, es decir, los cursos de la carrera de bachillerato y licenciatura en la Enseñanza de la Matemática con un alto contenido matemático e impartidos por profesores de la Escuela de Matemática (BLEM) de la UNA, durante el II ciclo, durante las dos primeras semanas del mes de octubre. No obstante, de una matrícula de 201 estudiantes del BLEM solo 92 respondieron el instrumento. Ningún estudiante negó información, pero debido a factores como abandono estudiantil, ausencia a clases, imposibilidad de algunos estudiantes de matricular cursos con código MAC a causa de falta de requisitos, entre otros, no fue posible aplicar el cuestionario a la totalidad del estudiantado matriculado en el ciclo lectivo.
El instrumento utilizado consta de dos partes. La primera, incorpora información general del estudiantado, como identificación, sexo, cursos matriculados, nivel educativo de los padres, entre otras variables de índole académica y familiar, con el fin de caracterizar la muestra. La segunda parte mide variables de autoeficacia matemática por medio de la Escala de Fuente de Autoeficacia en Matemática (EFAM) de Usher y Pajares (2009), adaptada al español por (Zalazar , Aparicio, Ramírez y Garrido, 2011)
La EFAM se basa en la teoría social cognitiva de Bandura (1977) y se subdivide en cuatro subescalas que son: experiencia directa, experiencia vicaria, persuasión verbal y factores fisiológicos. Los valores faltan- tes fueron imputados por la media de su respectiva subescala y la consistencia interna fue medida por medio del coeficiente alfa de Cronbach.
Análisis estadísticos
Se realizó una regresión múltiple, que es una técnica de análisis multivariado que permite estudiar la posible relación entre variables independientes, explicativas o predictoras y otra variable llamada de- pendiente o respuesta.
Para analizar los datos recolectados se utilizó el software gratuito y libre R, desarrollado por R Core Team (2013) versión © 3.6.0, en el cual se realizó la regresión múltiple que tomó como variable dependiente el rendimiento académico en matemática, operacionalizado como el promedio de los cursos con código MAC cursados por las personas estudiantes durante el segundo ciclo de 2019. Las variables independientes del modelo se subdividen en dos grupos: (a) las relacionadas con la autoeficacia matemática de acuerdo con la teoría de Bandura, representadas por las cuatro subescalas de la EFAM y (b) las variables personales y del contexto que pueden afectar el rendimiento académico en los cursos como el sexo, la condición de beca, la elección del BLEM como primera opción de carrera, el nivel educativo de la madre, el nivel en que se ubica la persona estudiante en el BLEM y si la persona ha reprobado algún curso del BLEM.
Los datos y el código que generaron los resultados de este artículo se pueden consultar en la plataforma de R Studio Cloud en el sitio https://rstudio.cloud/project/893958; es importante recordar que la persona interesada en acceder a los datos debe contar previamente con una cuenta de R Studio Cloud, si no la posee puede crear una al registrarse en la plataforma en la dirección https://rstudio.cloud.
Resultados
Estadísticas descriptivas
Las principales características de las personas participantes en el estudio se presentan en la tabla 1. Se observa que prácticamente no existe diferencia en el promedio de notas entre hombres y mujeres, la mayoría del estudiantado se encuentra en primero o segundo nivel de carrera, lo que posiblemente se deba a que 65,22% de los estudiantes a reprobado al menos un curso. Además, en cuanto al nivel educativo de los padres, predominan los niveles de primaria y secundaria; sin embargo, los mejores promedios son obtenidos por estudiantes cuyos progenitores poseen grado universitario. Asimismo, hay un alto porcentaje de estudiantes que decidieron como primera opción estudiar la carrera de BLEM y como institución de formación a la UNA; no obstante, el promedio de quienes eligieron al BLEM como su primera opción es menor. Finalmente, aunque la mayoría del estudiantado posee beca, en el promedio de notas es similar con respecto a quienes no la poseen. Ver Tabla 1.
Tabla 1. Frecuencia,promedio y desviación estándar de las principales variables sociodemográficas y académicas de estudiantes del BLEM. II ciclo 2019
| Variable | Cantidad | Promedio | sd |
| Sexo | |||
| Hombre | 50 | 74,28 | 10,43 |
| Mujer | 42 | 74,55 | 10,62 |
| La carrera BLEM fue su primera opción | |||
| Sí | 67 | 73,26 | 11,21 |
| No | 25 | 77,28 | 7,46 |
| Nivel educativo de la madre | |||
| Primaria | 32 | 73,57 | 10,46 |
| Secundaria | 38 | 73,95 | 11,12 |
| Universidad | 22 | 76,42 | 9,43 |
| Nivel educativo del padre | |||
| Primaria | 26 | 71,09 | 11,52 |
| Secundaria | 35 | 73,99 | 10,99 |
| Universidad | 21 | 77,44 | 8,65 |
| Ha reprobado algún curso | |||
| Si | 60 | 71,35 | 9,77 |
| No | 32 | 80,14 | 9,35 |
| La UNA fue su primera opción | |||
| Si | 62 | 75,32 | 11,42 |
| No | 30 | 72,53 | 7,97 |
| Nivel | |||
| I | 32 | 76,8 | 12,5 |
| II | 47 | 71,86 | 9,27 |
| III | 13 | 77,72 | 6,64 |
| Posee beca | |||
| Si | 62 | 74,2 | 9,70 |
| No | 30 | 74,83 | 12,04 |
Fuente: Elaboración propia (2020).
Consistencia interna de las escalas
En lo referente a las subescalas de autoeficacia, todas poseen coeficientes alfa mayores a 0,70 por lo que se considera que tienen una adecuada consistencia interna para los fines de la investigación. Ver tabla 2.
Tabla 2 Coeficiente alfa y su intervalo de confianza para las subescalas de autoeficacia de Usher y Pajares
| Subescala | Alpha de Cronbach | Intervalo de confianza | Promedio |
| Experiencia directa | 0,72 | 0,63 a 0,81 | 20,815 |
| Experiencia vicaria | 0,77 | 0,70 a 0,84 | 23,630 |
| Persuasión verbal | 0,84 | 0,79 a 0,89 | 22,523 |
| Estados fisiológicos | 0,84 | 0,80 a 0,89 | 22,239 |
Fuente: Elaboración propia (2020).
Modelo de regresión múltiple propuesto
La tabla 3 muestra los resultados del modelo de regresión. Es importante mencionar que el valor B representa los coeficientes de regresión no estandarizados los cuales, para efecto de interpretación, están dados en las mismas unidades de medida de las variables en el modelo; por lo que dependen de la escala en que se mide cada predictor.
En contraste, los coeficientes estandarizados Beta son directamente comparables ya que poseen la misma unidad de medida, lo cual permite comparar su importancia relativa con respecto a la variable dependiente. Cabe resaltar, como lo mencionan Montero Rojas, Villalobos Palma y Valverde Bermúdez (2007), que la importancia práctica de un predictor se asocia con el grado en que la persona investigadora considera el resultado como relevante, teniendo en cuenta el objeto de estudio y su contexto. Por tanto, aunque no es lo mismo significancia estadística que importancia práctica de una variable, en la medida que la primera representa que tan generalizable son los resultados y la segunda se asocia con qué tanto modifica la variable dependiente cada regresor de manera comparativa; los investigadores del estudio juzgan que un predictor tiene importancia práctica si su coeficiente Beta es mayor a 0,10 en valor absoluto.
Se verificaron los supuestos del modelo, normalidad (Anderson - Darling A=0,524, p=0,177), homocedasticidad (Breusch-Pagan, BP=19,719, p=0,073), independencia de los errores (Durbin-Watson, DW=1,922, p=0,582) y multicolinealidad, todos los valores VIF se encuentran entre 1,101 y 1,615. Además, el valor es de F =3,982 con un p<0,001 y se obtuvo un R cuadrado de 0,377 (R cuadrado ajustado de 0,282). Ver Tabla 3.
Tabla 3 Coeficientes no estandarizados y estandarizados del modelo de regresión múltiple para el rendimiento académico en cursos de matemáticas
| B | Beta | Error Estándar | Valor t | Valor p | ||
|---|---|---|---|---|---|---|
| Intercepto | 52,442 | 0,000 | 8,701 | 6,027 | 5,03e-08 | |
| Sexo (masculino) | -4,367 | -0,209 | 2,137 | -2,043 | 0,044 | ** |
| Beca | 2,712 | 0,122 | 2,145 | 1,264 | 0,209 | * |
| NEM (secundaria) | 0,517 | 0,024 | 2,186 | 0,237 | 0,814 | |
| NEM (universidad) | 3,649 | 0,149 | 2,781 | 1,312 | 0,193 | * |
| BLEM | -4,514 | -0,193 | 2,178 | -2,072 | 0,0415 | ** |
| Experiencia directa | 0,699 | 0,229 | 0,343 | 2,037 | 0,044 | ** |
| Experiencia vicaria | 0,437 | 0,145 | 0,326 | 1,341 | 0,183 | * |
| Persuasión verbal | -0,012 | -0,005 | 0,241 | -0,052 | 0,958 | |
| Factores fisiológicos | 0,299 | 0,148 | 0,200 | 1,494 | 0,139 | * |
| Nivel II | -4,272 | -0,205 | 2,187 | -1,953 | 0,054 | * |
| Nivel III | 2,912 | 0,097 | 3,003 | 0,970 | 0,335 | |
| Reprobar | -7,372 | -0,337 | 2,079 | -3,546 | 6,61e-04 | ** |
* El predictor posee un coeficiente Beta mayor a 0,10
** El predictor posee un coeficiente Beta mayor a 0,10 y un valor p menor a 0,05
Fuente: Elaboración propia (2020).
En la tabla 3 se aprecia como las diferentes subescalas de autoeficacia se relacionan positivamente con el RAM, siendo la más importante la experiencia directa (p =0,044) y las otras tienen una importancia práctica, a excepción de la persuasión verbal, la cual no mostró ser relevante. Estos resultados concuerdan con otros estudios sobre el tema, en los que se muestra como la experiencia directa es la principal
dimensión de la escala de autoeficacia y la persuasión verbal suele tener bajo poder predictivo en lo que respecta a rendimiento académico (Bandura, 1977, 1993).
Como era de esperar el estudiantado que ha reprobado algún curso universitario muestra un RAM menor (p<0,001) y, a pesar de no ser significativo, el coeficiente de tenencia de beca resulta relevante (Beta =0,122) en favor de la personas estudiantes que poseen este beneficio, lo cual muestra la importancia de la beca como predictor del rendimiento (Salinas Oviedo, Hernández, & Barboza-Palomino, 2017). De igual forma, como revelan varios estudios (Chaparro Caso López, González Barbera y Caso Niebla, 2016; Fajardo Bullón, Maestre Campos, Felipe Castaño, León del Barco y Polo del Río, 2017; Rodríguez-Pineda, 2018) el nivel de estudios de la madre (NEM) posee importancia práctica y su coeficiente muestra un mejor RAM en estudiantes con madres universitarias en comparación con quienes tienen progenitoras con solamente estudios primarios (Beta=0,149), manteniendo todas las demás variables constantes.
Por otra parte, aunque el coeficiente para el sexo resultó significativo, la diferencia en valor absoluto de los promedios es prácticamente nula (ver tabla 1), por lo que a pesar de ser significativo no podría decirse que el RAM favorezca a ninguno de los sexos. Finalmente, se observa que los estudiantes que decidieron cursar el BLEM como primera carrera poseen un RAM inferior (Beta =-0,193), en particular los que cursan el segundo año del plan de estudios (Beta=-0,205).
Discusión y conclusiones
Uno de los objetivos del estudio es mostrar la importancia de la autoeficacia matemática en el rendimiento académico de estudiantes en una carrera de Enseñanza de la Matemática. Los resultados efectivamente muestran la relevancia del constructo en el RAM, especialmente el de la experiencia directa y aunque las dimensiones de experiencia vicaria y los estados fisiológicos no resultaron significativos, tienen un coeficiente estandarizado que sugiere su importancia relativa en comparación con otros predictores (ver tabla 3). Lo anterior concuerda con lo esperado, pues por lo general los estudiantes del BLEM eligen la carrera por considerarse con buenas capacidades lógico-matemáticas, basados en sus experiencias en la educación secundaria (Bandura, 1977, 1993; Echeverría Castro, Sotelo Castillo, Acosta Quiroz y Barrera Hernández, 2020).
Por el contrario, la persuasión verbal no mostró ser relevante para predecir el RAM, lo cual es consecuente con otros estudios (Canto, 1998; Echeverría Castro et al., 2020; Zalazar et al., 2011), los cuales muestran un comportamiento similar a esta escala. Asimismo, aunque algunas investigaciones han sugerido un mejor RAM de los hombres con respecto a las mujeres, los promedios en cursos de código MAC en el BLEM no muestra diferencia a nivel de sexo; a pesar de ello el coeficiente resulta significativo y ligera- mente favorable a las mujeres; sin embargo, se considera que no existe suficiente evidencia para decir que las féminas muestran un mejor RAM.
El resultado ilustra la importancia de considerar diferentes indicadores a la hora de interpretar una cifra, pues como la ASA (American Statistical Association) menciona el valor p no debería ser el único criterio para tomar decisiones acerca de un fenómeno (Wasserstein y Lazar, 2016). Asimismo, es posible que la presencia de una variable de confusión influya en el coeficiente del sexo, por lo que se recomienda que futuras investigaciones profundicen en la relación entre esta variable y el rendimiento académico en contextos matemáticos.
Por otra parte, a pesar de no ser significativo, la variable tenencia de beca muestra cierta relevancia práctica (Beta=0,122), ya que poseer beca aumenta el RAM en 2,71 puntos. Una posibilidad para este comportamiento es que las personas becadas en la institución se sienten comprometidas a obtener un mayor rendimiento académico para mantener el beneficio, es decir, es un incentivo para obtener buenas altas calificaciones (Rodríguez-Pineda y Zamora-Araya, 2014; Soto , Díaz y Chiang 2017).
Asimismo, el NEM muestra poseer importancia en su relación con el RAM, pues si la progenitora tiene un grado universitario mayor es el rendimiento del estudiantado en comparación con el de madres que poseen solo educación primaria, donde se mantienen el resto de las variables del modelo constantes; es decir, incluso para personas con idéntico nivel de autoeficacia matemática, el capital cultural del hogar resulta ser relevante a la hora de explicar el rendimiento académico (Bourdieu, 2015; Bourdieu y Passeron, 1977; Zamora-Araya, 2020).
Por otra parte, las personas estudiantes que seleccionaron al BLEM como su primera opción de carrera, en promedio obtienen 4,514 puntos menos que los que no eligieron a BLEM como primera opción (p=0,041), lo cual es un resultado inesperado ya que se esperaba un mayor desempeño en estudiantes cuya carrera de preferencia fuese el BLEM. Una posible explicación para este comportamiento podría radicar en que las expectativas del estudiantado cuando ingresa al BLEM, en cuanto a los contenidos matemáticos y su forma de abordarlos, no siempre coinciden con lo desarrollado en los cursos; muchas veces las personas estudiantes que ingresan al BLEM piensan que es suficiente con ser “buenos (as)” estudiantes en matemáticas para ser docentes de la asignatura y el trabajo docente requiere de muchas otras habilidades (Calderón, 2014; Zamora-Araya y Villalobos-Madrigal, 2018b).
Adicionalmente, los datos muestran que los estudiantes de segundo nivel muestran un rendimiento menor en comparación a los estudiantes de primer nivel (p = 0,054, Beta = -0,205). El resultado tampoco coincide con lo esperado, pues se suponía que con el paso de los semestres el estudiantado mejoraría su rendimiento, debido a la madurez y experiencia obtenida en los cursos previos (Gómez , Oviedo y Martínez 2011). Sin embargo, la malla curricular del BLEM incluye solo una materia por ciclo de código MAC durante el primer año de cursos, y a partir del segundo nivel incluye dos materias de este tipo, por lo que la exigencia para las personas estudiantes en segundo nivel es mayor que para las de primer nivel, lo que explicaría en parte la baja en el RAM.
Por otra parte, como lo muestran otros estudios, se confirmó la hipótesis de que el estudiantado que reprueba cursos poseen un rendimiento menor en comparación a quienes no reprueban, en promedio 7,37 puntos menos (p<0,001), ya que la variable está muy relacionada con la experiencia directa, en relación con las expectativas de dominio del individuo (Bandura, 1993; Canto, 1998).
En resumen, se evidencia la importancia de la autoeficacia matemática como predictor en el RAM en los estudiantes del BLEM de la UNA y, como era de esperar, las experiencias propias de la persona cobran importancia al explicar el RAM. Del mismo modo, las variables sexo, tenencia de beca, nivel educativo de los padres, elección de carrera, nivel de carrera y condición de reprobación, mostraron ser relevantes como predictores del RAM en el estudiantado del BLEM de la UNA.
Finalmente, se espera que el trabajo contribuya a evidenciar la importancia del constructo de la auto- eficacia matemática en estudiantes que cursan carreras con alto contenido matemático como el BLEM. Asimismo, es necesario continuar con investigaciones referentes a otros aspectos relacionados con el RAM como lo son los aspectos vocacionales, pues en ocasiones las personas estudiantes carecen de información sobre lo que implica cursar una carrera como el BLEM, la cual requiere tanto de gusto por la matemática como por la enseñanza. Además, los datos muestran lo necesario de considerar otros indicadores, además de los valores p, tales como las medidas de tamaño de efecto para poder interpretar de manera más apropiada los resultados de un análisis estadístico en un contexto educativo.