Introducción
En Chile, la Ley 20.903 establece exigencias para asegurar una formación de calidad para los futuros profesores. En particular, desde el 2019, tanto las universidades como sus carreras y programas de pedagogía deben estar acreditados de acuerdo con los criterios de calidad establecidos por la Comisión Nacional de Acreditación (CNA, 2014). Entre ellos, se destaca la importancia de la línea de formación práctica, que incluye el acercamiento al contexto escolar real mediante las denominadas prácticas tempranas, en el proceso educativo, y cómo las instituciones deberán asegurar tanto su calidad como su cumplimiento. Cabe mencionar que la práctica profesional es la instancia final de la formación práctica en la educación universitaria chilena y se encuentra en el último año de la instrucción de profesores.
La formación aludida contempla instancias de prácticas pedagógicas tempranas, en las cuales el futuro profesor (FP) debe poner en juego sus conocimientos profesionales para el diseño de tareas de enseñanza-aprendizaje, en general, con una progresión gradual en el tipo de intervenciones y en el acercamiento con el contexto escolar. Se espera que vaya integrando conocimientos disciplinares (matemáticos) y didácticos disciplinares (didáctico-matemático), para comprender el contexto escolar y los procesos de enseñanza-aprendizaje de los que serán parte (MINEDUC, 2021).
De acuerdo con Pino-Fan et al. (2018), las competencias que los profesores de matemática adquieren durante su formación universitaria no necesariamente se transfieren a las prácticas, asunto que motiva la indagación sobre cómo son llevados a cabo los procesos e instancias de prácticas tempranas y cómo se integran en ellas los conocimientos profesionales. En este sentido, existen investigaciones dedicadas a estudiar esa parte de la formación de profesores (e. g. Pino-Fan et al., 2018; Pino-Fan y Godino, 2015; Jiménez et al., 2014; Pino-Fan et al., 2022). En particular, Pino-Fan et al. (2018) señalan que los estándares orientadores para la preparación docente, propuestos por el MINEDUC (2012), establecen una separación entre lo disciplinario y lo pedagógico. Esto da paso a una desconexión entre las distintas dimensiones del conocimiento didáctico disciplinar, necesarias para la gestión apropiada de los aprendizajes de sus estudiantes, lo que supone un riesgo en el logro efectivo de las habilidades escolares.
Por su parte, la nueva propuesta de estándares de la profesión docente (MINEDUC, 2021) contempla los conocimientos disciplinares y los didácticos disciplinares específicos para cada eje temático que se espera del profesor al final de la formación inicial docente (FID). En el caso de matemáticas, entre su conocimiento didáctico disciplinar se considera que el docente pueda diseñar planes de clases, los cuales aborden el desarrollo de las habilidades (resolución de problemas; argumentar y comunicar; modelar y representar) que se contemplan en el currículum oficial (MINEDUC, 2016a; 2019). Este último, con una actualización reciente, plantea nuevos desafíos para la FID, ya que aumenta los requerimientos sobre los conocimientos profesionales del profesorado, al poner ''énfasis en el desarrollo de habilidades propias de la disciplina en los estudiantes''(MINEDUC, 2021, p. 14).
Concordamos con De Oliveira y Cerqueira (2021) sobre la necesidad de reforzar un lente crítico en la verificación de cómo se están llevando a cabo las reformas curriculares en los distintos dominios de habilidades propuestas. Al respecto, pareciera ser una preocupación el estudio del desarrollo de las distintas habilidades a escala mundial (e. g. Ramos, Herrera y Ramírez, 2010; Zurita, 2020; Reed, 2007), puesto que estas conllevan la implementación de distintas competencias establecidas tanto en la secundaria como en el nivel superior.
Particularmente, podría existir una atención especial y una constante vigilancia sobre la formación de los FP desde tres puntos de vista: lo que estos deben aprender (MINEDUC, 2021), lo que enseñan durante sus prácticas (Calderón, 2020) y aquello que están efectivamente aprendiendo (Grossman, 2011; Cisternas 2011). Este trabajo se enfoca en aquello que el FP enseña durante su práctica profesional, como primera aproximación y experiencia al ejercicio docente en un contexto auténtico, lo que, según Grossman et al. (2009), es una dimensión central para el aprendizaje de habilidades, conocimientos y actitudes que este debe potenciar en sus estudiantes (Breda et al., 2016). Adicionalmente, Barber y Mourshed (2007), Paquay et al. (1996) y Zeichner (2010) aseguran que gran parte del aprendizaje del conocimiento pedagógico y disciplinar se logra mediante la observación y el desarrollo de estas prácticas. De tal modo, en este escrito nos centramos en el contexto de la práctica profesional, ya que es la última instancia en la formación inicial del profesor, en la que se espera la integración de aquellos conocimientos especializados en el real ejercicio docente.
En relación con la propuesta realizada por el MINEDUC (2016b; 2019) con respecto al desarrollo de las habilidades matemáticas, tal como señala Breda et al. (2016), el propósito de los programas sugeridos para el desarrollo profesional del profesorado de matemáticas es mejorar la enseñanza de la materia, en la cual dicha mejoría se ha visto vinculada al seguimiento de ciertas tendencias, derivadas de las investigaciones y publicaciones en educación matemática, generando corrientes que se ''cristalizan en los currículos de diferentes países, en forma de lineamientos y principios que nos dicen, a priori, cómo tener una educación matemática de calidad''(p. 56). De esto, y observando la propuesta ministerial, se asume que, al fomentar el desarrollo de las habilidades disciplinares incluidas en el documento oficial, se está impartiendo educación de calidad, lo que motiva a poner el foco de atención sobre la FID y en cómo los futuros profesores proponen el desenvolvimiento de habilidades matemáticas en sus propuestas de enseñanza.
En concordancia con lo importante de las prácticas y en relación con los criterios de calidad en la formación de profesores de matemática, establecidos por la CNA, este trabajo pretende caracterizar el quehacer matemático que fomenta el profesor en el aula de clases, el cual aquí se particulariza en términos de las habilidades matemáticas que el futuro profesor espera desarrollar en sus estudiantes en el contexto de la formación práctica de la FID. Para atender a este objetivo, nos planteamos la siguiente pregunta: ¿cómo el futuro profesor aborda el desarrollo de las habilidades matemáticas establecidas por el MINEDUC (2016a; 2019) durante la enseñanza, en el contexto de su práctica profesional?
Marco teórico
En virtud del objetivo y la pregunta que guían nuestro trabajo, el marco teórico lo hemos conformado por dos ejes; el primero contempla las definiciones de las habilidades matemáticas establecidas en el currículo chileno y el segundo es el modelo de los espacios de trabajo matemático (Kuzniak, 2011), que describimos a continuación.
Habilidades del currículum escolar chileno
En el 2016, el Ministerio de Educación de Chile (MINEDUC, 2016a) actualizó las bases curriculares de matemáticas que establecen objetivos de aprendizaje para los niveles de 7.º básico (12-13 años) y 2.º medio (15-16 años), los cuales se enmarcan en el desarrollo de cuatro habilidades disciplinares o del pensamiento matemático: resolver problemas; argumentar y comunicar; modelar y representar. De acuerdo con estas bases, dichas habilidades están contempladas para desenvolverse a lo largo de los 12 años de escolaridad obligatoria chilena (MINEDUC, 2012; 2016a; 2019), a través de propuestas de enseñanza que el propio currículo entrega a los docentes, a modo de orientaciones.
Los documentos anteriormente señalados (e. g. MINEDUC, 2016a) describen las habilidades como sigue:
Resolver problemas. Se expresa cuando un estudiante logra solucionar una situación problemática dada, sin que se le haya indicado un procedimiento por seguir. Los alumnos experimentan, luego seleccionan o diseñan estrategias (ensayo y error; metaforización o representación; simulación; transferencia desde problemas similares ya resueltos, etc.) para aplicarlas. Finalmente, comparan diferentes vías resolutivas y evalúan las respuestas obtenidas en el marco de los desafíos.
Modelar. Constituye el proceso de utilizar y aplicar modelos, seleccionarlos, modificarlos y construir otros modelos matemáticos, identificando patrones característicos de situaciones, objetos o fenómenos que se desea estudiar o resolver, para finalmente evaluarlos. Se manifiesta cuando el estudiante puede construir una versión simplificada y abstracta de un sistema más complejo, que capture los patrones claves, y que lo exprese mediante lenguaje matemático. Por medio de la modelización matemática, los alumnos aprenden a utilizar una variedad de representaciones de datos, a seleccionar y aplicar métodos matemáticos apropiados o herramientas para resolver problemas del mundo real. El currículo chileno utiliza el término 'modelar', en lugar de 'modelizar', con el fin de expresar la construcción de modelos matemáticos.
Representar. Se manifiesta cuando el estudiante transita desde un ámbito más concreto y cotidiano hacia otro más abstracto como el lenguaje simbólico. En este sentido, son claves las metáforas, analogías con experiencias concretas y representaciones semióticas, que facilitan la comprensión del nuevo ámbito abstracto en el cual habitan los conceptos que se están construyendo o aprendiendo y permiten relacionar el conocimiento intuitivo con una explicación formal. Así, se espera que los alumnos se adapten a las necesidades de la situación o actividad, extrayendo la información que proporciona el entorno y eligiendo las formas de expresar esos datos (tablas, gráficos, diagramas, metáforas, símbolos matemáticos, etc.).
Argumentar y comunicar. Se observa cuando el estudiante, al descubrir inductivamente regularidades y patrones en sistemas naturales y matemáticos, trata de convencer a otros de su validez, estimulado a utilizar un amplio abanico de modos comunicativos de sus ideas, incluyendo metáforas y representaciones. Es importante que los alumnos puedan argumentar y discutir, en instancias colectivas, así como escuchar y retroalimentar mutuamente sus soluciones a diversos problemas. Se espera que diferencien entre argumentación intuitiva y matemática, sean capaces de verbalizar sus intuiciones y concluyan correctamente, apoyados en diferentes representaciones (fortaleciendo las competencias de expresión y comunicabilidad, la escucha activa, la creatividad y la actitud reflexiva).
Como se observa en la descripción de estas habilidades, cada una contempla otras para su expresión y desarrollo. De este modo, MINEDUC (2016b) muestra que estas se desarrollan de manera integrada; por ejemplo, en una actividad que busca modelizar una situación, con base en un problema, se encuentran implicadas la representación en diferentes niveles (concreto, pictórico y simbólico) y la argumentación respecto de la validez del modelo construido.
Espacios de trabajo matemático
Las orientaciones docentes que ofrece el currículo chileno (MINEDUC, 2016a) indican que las propuestas de enseñanza se basan, principalmente, en conjuntos de tareas planteadas para el trabajo de los estudiantes, focalizadas en atender cierto objetivo de aprendizaje, conocimiento matemático y desarrollar habilidades cognitivas. Por su parte, Ramos, Herrera y Ramírez (2010) señalan que esas últimas corresponden a las destrezas y procesos de la mente necesarios para realizar una tarea. Además, ellas son facilitadoras del conocimiento y responsables tanto de adquirirlo como de recuperarlo para que se utilice posteriormente (Reed, 2007). En esta investigación, reconocemos que no existe un consenso en la definición de tarea, por lo que adoptamos lo señalado por Henríquez-Rivas et al. (2021), quienes la indican como ''una experiencia matemática planificada para los estudiantes, que puede ser una acción o una secuencia de acciones''(p. 127). Lo anterior se acomoda a la temática expuesta y a los objetivos de este escrito.
La relación entre tareas y habilidades nos permite examinar aquellas tareas que se orientan al trabajo matemático y estudiarlas desde las habilidades que requieren y permiten desarrollar. En este aspecto, seleccionamos el modelo del espacio de trabajo matemático (Kuzniak, 2011) como herramienta para analizar las tareas propuestas por el FP, en el marco de su práctica final. A continuación, describimos su formulación y componentes.
El espacio de trabajo matemático (ETM) (Kuzniak, 2011; Gómez-Chacón, Kuzniak, Vivier, 2016) tiene por objetivo principal modelizar la labor matemática en un contexto educativo, por medio de una tarea matemática dada, con el fin de favorecer y mejorar las condiciones en las que se produce el proceso de enseñanza-aprendizaje de las matemáticas. Para definir los ETM, se introducen dos planos horizontales, uno epistemológico y otro cognitivo, los cuales, a su vez, incluyen tres componentes cada uno. El plano epistemológico está constituido por el referencial (formado por las propiedades, teoremas y definiciones), el representamen (signos semióticos) y artefactos (materiales o simbólicos). Por su parte, al plano cognitivo lo conforman los polos de visualización (relativa a la representación del espacio y al soporte material), la construcción (que depende de los instrumentos y técnicas asociadas) y la prueba (apoyada en el proceso discursivo de validación, basada en el referencial teórico). Dichos planos se conectan y articulan mediante distintas génesis:
Instrumental. Permite hacer operatorios a los artefactos en el proceso constructivo.
Semiótica. Se basa en los registros de representación semiótica que asegura a los objetos tangibles de los ETM su estatus de objetos matemáticos operatorios.
Discursiva. Da sentido a las propiedades, para ponerlas al servicio del razonamiento matemático.
Asimismo, el modelo del ETM considera tres planos verticales (Kuzniak y Richard, 2014), los cuales se activan por medio de una determinada tarea, cada uno definido por dos génesis: semiótico-instrumental (sem-ins); semiótico-discursivo (sem-dis) e instrumental-discursivo (ins-dis). Todo lo anterior permite la comprensión del trabajo matemático que se genera en torno a la resolución de una tarea.
Además, se identifican tres tipos de ETM: el de referencia, del cual depende la organización matemática, definida sobre la base de criterios matemáticos (alude al estudio de la teoría matemática); el idóneo, que consiste en el acondicionamiento y la organización del ETM de referencia, con el propósito de convertirlo en un espacio que permita el trabajo matemático en una institución educativa dada, con una función definida (se refiere a todo lo relacionado con la enseñanza); y el personal, que reside en la manera en que un individuo realiza el trabajo matemático basado en sus conocimientos y capacidades cognitivas (Kuzniak, 2011).
Del mismo modo, en esta indagación distinguimos el ETM idóneo implementado o actual del ETM idóneo previsto o potencial (Henríquez-Rivas et al., 2021); el primero referido a aquello que es ejecutado en y para el aula, relativo a la enseñanza, mientras que el segundo remite a aquello que el profesor espera se pueda efectuar durante la enseñanza.
Por otra parte, el ETM considera al término herramienta como aquello que puede utilizarse para resolver la tarea propuesta. Kuzniak et al. (2016) emplea este término para hacer alusión a los componentes del plano epistemológico que tienen un uso potencial a la hora de resolver un problema dado y que pueden estar asociados con el plano cognitivo por intermedio de algún instrumento. Según Kuzniak et al. (2016), el ETM contempla tres tipos de herramientas: las semióticas, que corresponden a herramientas no materiales para operar sobre representaciones semióticas de objetos matemáticos; las tecnológicas, artefactos como herramientas de dibujo, técnicas rutinarias basadas en algoritmos o calculadoras con algoritmos de cálculo, y las teóricas, que abarcan las propiedades de los objetos matemáticos, las cuales pertenecen al referencial de la tarea que se desea resolver. En tanto, Verdugo-Hernández (2018) añade a esta lista la noción de herramienta operacional, la cual alude a instrumentos teóricos requeridos para resolver cierta tarea, pero que no forman parte del referencial teórico al cual pertenece dicha tarea. Así, en cuanto al marco teórico, nuestro objetivo se traduce en caracterizar el trabajo matemático que el futuro profesor de matemática privilegia en el contexto de su práctica profesional, en relación con el desarrollo de las habilidades disciplinares establecidas por el MINEDUC para la asignatura de Matemáticas. Por tanto, nos preguntamos, ¿cómo el FP aborda el desarrollo de habilidades matemáticas establecidas por el MINEDUC (2016a; 2019), a través del trabajo matemático que privilegia durante la enseñanza en su práctica profesional?
Metodología
Para abordar nuestro objetivo, adoptamos un paradigma interpretativo con una metodología de corte cualitativo (Denzin y Lincoln, 2000). Se trata de un estudio de caso de tipo instrumental (Stake, 2007) en que el informante es un futuro profesor (FP) de matemática, al que llamaremos Lucas. Él se encuentra desarrollando el curso de práctica profesional de último semestre de la carrera de Pedagogía en Educación Media en Matemática, en una universidad chilena. El curso de práctica profesional implica la realización de 30 horas semanales en un establecimiento educacional, por aproximadamente tres meses. En ese período, el FP debe asumir funciones propias de los docentes, como planificar e implementar propuestas de enseñanza.
El centro de práctica que ha sido asignado a Lucas corresponde a un liceo subvencionado por el Estado de Chile, que tiene entre 30 y 40 estudiantes por curso. El FP es acompañado y supervisado por dos docentes; en el liceo, por un profesor de la disciplina, en el rol de guía, y en la universidad, por quien está a cargo del curso de práctica como tutor. Este último es especialista en didáctica de la matemática. Lucas distribuye sus 30 horas de práctica en distintos cursos de 7.° a 4.° medio. En este estudio hemos seleccionado el trabajo realizado en el curso de 1.º medio (de 14 a 15 años).
El contexto del trabajo de práctica profesional contempló distintas fases para Lucas, las cuales mostramos a continuación:
Fase 1: Dos semanas de adaptación al centro de práctica y de observación de las clases de matemática impartidas por el profesor guía. Fase 2: Planificación de la enseñanza de una unidad temática, adecuada al formato del centro de práctica. Fase 3: Implementación de las clases planificadas, supervisadas por el guía y monitoreadas por el tutor. Fase 4: Supervisión, por parte del tutor, del desarrollo de las clases implementadas. Fase 5: Confección de un cuaderno de bitácoras con reflexiones sobre las clases realizadas, actualizado semanalmente por el FP. Fase 6: Reuniones de coordinación y de retroalimentaciones con el guía del centro de práctica. Fase 7: Reuniones de retroalimentación con el tutor.
Esta práctica profesional se realizó en contexto de la pandemia a causa del COVID-19, lo que llevó a adaptar el tipo de interacción entre estudiantes y profesores, tanto en el centro de práctica como en el desarrollo del curso de práctica en la universidad. Lucas implementó la enseñanza mediante clases sincrónicas y asincrónicas, a distancia y en línea, a través de una plataforma digital (Google Meet). Además, la universidad contó con una plataforma institucional, donde el FP debía almacenar y organizar todos los materiales diseñados para su práctica, entre ellos, su cuaderno de bitácora y planificaciones, los que fueron retroalimentados oportunamente por el tutor (fase 7).
Selección del caso
El caso de Lucas ha sido seleccionado debido a que es representativo (Yin, 2009) con respecto a los otros practicantes. Lucas efectuó 17 clases correspondientes al curso de 1.° medio. Todas las sesiones fueron acompañadas y monitoreadas por el guía y tres de ellas fueron supervisadas por el tutor (clases 10, 11 y 12). En dichas supervisiones de clases, fue posible identificar, preliminarmente, una clara tendencia al desarrollo de la habilidad que nos interesa, asunto que está también declarado en sus planificaciones.
Para este trabajo, presentamos el análisis de la primera clase, ya que es rica en evidencias respecto del tema que nos interesa estudiar y presenta características comunes en relación con la estructura de las otras (Coyne, 1997). Adicionalmente, se contemplan las fases 2, 3 y 5 del proceso de práctica profesional de Lucas.
Recolección y análisis de datos
Para establecer características del espacio de trabajo de matemática del futuro profesor, nos basaremos en el ETM idóneo.
En esta oportunidad, nos referiremos al ETM idóneo implementado por el futuro profesor (ETMi del FP), que corresponde al trabajo matemático sobre las clases efectivamente realizadas.
Los datos provienen, principalmente, de los videos de grabaciones de las clases y las planificaciones que Lucas desarrolló en el contexto de su práctica profesional y que fueron supervisadas por el tutor. Adicionalmente, se consideró la bitácora en la cual Lucas registró su reflexión sobre sus implementaciones, como una fuente secundaria de datos.
Con el propósito de reducir, organizar y dar significado a la información, Burns y Grove (2004) señalan que el análisis de los datos cualitativos consta de tres etapas: descripción, análisis e interpretación. En primer lugar, se realizó una descripción del trabajo implementado en las clases, las cuales han sido divididas en tres episodios: inicio, desarrollo y cierre, identificando aquellas tareas matemáticas que propician el desenvolvimiento de alguna de las habilidades establecidas por el MINEDUC, siguiendo el protocolo establecido en la tabla 1.
Tabla 1 Protocolo de identificación de tareas que promuevan habilidades
| Habilidades observadas | |
|---|---|
| Identificación de habilidades | Descriptor |
| Resolver problemas (RP) | Entenderemos que el profesor estará desarrollando la habilidad de ''resolver problemas”, cuando presente al estudiante una tarea en la que se refleje una situación con un contexto dado, con las siguientes características: que el problema tenga una respuesta, que permita el ensayo y error, que permita alguna transferencia desde problemas similares ya resueltos. |
| Modelar (M) | Entenderemos que el profesor estará desarrollando la habilidad de ''modelar”, cuando presente al estudiante una tarea en la cual se observe un problema basado en el mundo real, se puedan extraer variables, capturar patrones claves que sea posible expresar en lenguaje matemático, etc. |
| Representar (R) | Entenderemos que el profesor estará desarrollando la habilidad de ''representar”, cuando presente al estudiante una tarea en la que se involucre traspasar la realidad desde un ámbito más concreto y familiar a otro más abstracto. |
| Argumentar y comunicar (AC) | Entenderemos que el profesor estará desarrollando la habilidad de ''argumentar y comunicar”, cuando presente al estudiante una tarea que otorgue las herramientas necesarias para que pueda descubrir inductivamente regularidades y patrones en sistemas naturales matemáticos y trate de convencer a otros de su validez. |
Nota: Fuente propia de la investigación.
En segundo lugar, para el análisis del ETMi, se recurrió a los descriptores contenidos en la tabla 2, relativos a los componentes del ETM, para caracterizar el trabajo matemático que Lucas promovía durante la clase a través de la selección y del planteamiento de tareas.
En tercer lugar, para la interpretación de los hallazgos, se integró el análisis del ETM en las tareas propuestas con la identificación de las habilidades que ellas involucran. Con esto, se buscó dar respuesta a la pregunta de investigación, mediante las relaciones identificadas entre las habilidades y el trabajo matemático presentes en la práctica de Lucas.
Análisis y resultados
Descripción de la clase
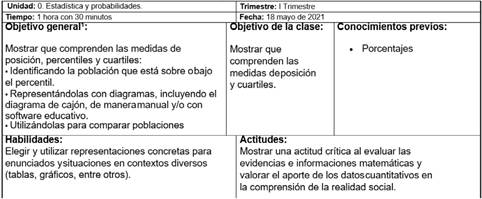
En la clase observada, Lucas tiene por objetivo mostrar que los estudiantes comprendan las medidas de posición y cuartiles, en el eje de probabilidad y estadística para 8.º año de enseñanza básica (MINEDUC, 2016a) (ver figura 2). Este objetivo se estableció en la fase 2 de planificación
Tabla 2 Protocolo para el análisis de los componentes y herramientas del ETM
| Espacio de trabajo matemático | |||
|---|---|---|---|
| Criterio | Componente | Herramienta | Descriptor |
| Plano epistemológico | Referencial | Herramienta teórica | Se identifica como aquellas propiedades que nos sirven para resolver una determinada tarea de un mismo referencial. |
| Herramienta operacional | Se identifica cuando el profesor utiliza ciertas propiedades o teoremas que corresponden a otro referencial. | ||
| Artefactos | Herramienta tecnológica | Corresponde a aquellos instrumentos relativos a algún tipo de software. | |
| Representamen | Herramienta semiótica | Se puede observar cuando el profesor escribe un signo, haciendo alusión a una noción matemática. | |
| Por ejemplo, cuando escribe an + 1 ≥ an refiriéndose a la sucesión monótona creciente. | |||
| Plano Cognitivo | Prueba | Corresponde al razonamiento discursivo que se basa en una prueba (pragmática, intelectual). | |
| Construcción | Se basa en las acciones desencadenadas por los artefactos utilizados y las técnicas de uso asociadas. | ||
| Visualización | Interpreta y relaciona los objetos matemáticos, según actividades cognitivas vinculadas con los registros de representación semiótica (identificación, tratamientos, conversión). | ||
Nota: Fuente propia de la investigación.
y se registró en la bitácora (fase 5). Cabe señalar que las planificaciones de la sesión se realizaron según el formato establecido por el establecimiento educacional y bajo la supervisión del guía.
La planificación diseñada por Lucas (figura 2) busca desarrollar la habilidad de ''representar''en contextos diversos, con la utilización de tablas y gráficos, dejando un margen abierto respecto de otros tipos de representaciones por utilizar. Además, en los indicadores de logro del detalle de su planificación (ver figura 3), se observa que los estudiantes deberán ser capaces de representar las medidas de posición, por medio de diagrama de cajón, una vez terminada la unidad. Por otro lado, Lucas indica que se apoyará en el uso de Power Point, dejando fuera otro tipo de software o recurso.
Durante el primer episodio, Lucas inicia su clase de forma virtual-sincrónica, presentando una tarea introductoria (figura 4). Esta busca activar el conocimiento previo de los estudiantes sobre porcentaje, asunto contemplado en la planificación.
Dicha tarea está contextualizada y es cercana para los estudiantes, debido a que la red social ''Instagram''es ampliamente conocida por ellos y manejan los términos que utiliza (seguidores, cuenta y red social). En esta instancia, los alumnos presentan baja participación en sus respuestas y es el FP quien responde las preguntas planteadas.
A continuación, en el episodio desarrollo de la clase, Lucas define las medidas de posición como aquellas que ''dividen a un conjunto de datos ordenados en una cantidad determinada de partes iguales, por
tanto, es aplicable para las variables cuantitativas''(ver figura 5a). A lo anterior, añade la definición de variables cuantitativas, como esas a las que se les puede asociar un valor numérico, y la de medidas de posición, específicamente, los cuartiles, como los valores que dividen una muestra de datos en 4 partes iguales (ver figura 5b).
Luego, Lucas expone la fórmula con el propósito de determinar la posición de los cuartiles, basándose en esta para trabajar en el problema propuesto (figura 6), sin desarrollar la fórmula o poder deducir junto a sus estudiantes.
En este episodio, se observa una intención, por parte de Lucas, de generar un diálogo con los alumnos, realizando preguntas sobre la fórmula recién presentada. Ellos responden con lo que Lucas ha mencionado durante su presentación.
FP: ¿Cómo calculamos los cuartiles? ¿Qué es n? ¿Qué era k?
E1: n es el número de total de datos
E2: k es 1, 2 y 3
Por otra parte, ninguno de los estudiantes se cuestiona sobre las variables involucradas en la fórmula. Luego de esto, Lucas les presenta dos tareas más: una similar a lo visto en la figura 6 y otra que incluye el diagrama de caja y bigotes (ver figura 7). En ambas se insiste en la aplicación de la fórmula para calcular cuartiles (mediante una nube tipo recordatorio en la figura 7a)
y se solicita el cálculo de dos de ellos. Pese a que las indicaciones estipuladas son para los alumnos, resulta ser Lucas quien nuevamente las realiza.
Posterior a la tarea de construir el diagrama de caja y bigotes, el FP plantea otras dos más. La primera (figura 8a) busca que los estudiantes ubiquen los distintos cuartiles. La segunda pretende que relacionen el diagrama de caja y bigotes con los datos presentados a la izquierda de la imagen 8b. Las tareas presentadas en las figuras 8a y 8b incluyen las notaciones usuales de los cuartiles y la representación del diagrama de caja y bigotes, de modo que los alumnos utilicen esas representaciones para resolverlas. En la 8a se pide ubicar los cuartiles en relación con el diagrama, mientras que en la 8b se pretende que el estudiante identifique el diagrama correspondiente a los datos proporcionados; esto es, extraer datos de la representación (diagrama de caja y bigotes) para poder dar respuesta a lo solicitado.
Finalmente, en el episodio de cierre de la sesión, Lucas vuelve a las diapositivas de su presentación, haciendo énfasis

Nota: Fuente propia de la investigación.
Figura 7 Problema de posición del cuartil y de caja y bigotes
en la fórmula de posición de los cuartiles, a modo de cierre, y luego la da por terminada. Para esta clase, en la fase 6 se sugiere a Lucas que sería deseable que hubiese desarrollado la fórmula, con el fin de determinar los cuartiles mediante alguna tarea, lo cual queda registrado en su bitácora como una de las reflexiones sobre la enseñanza en esta lección.
Retroalimentación del profesor guía del centro de práctica
En general, el guía realiza retroalimentaciones al FP semanalmente, mediante breves reuniones individuales y de forma remota (virtuales), en las cuales le asigna diferentes tipos de labores que debe cumplir durante los días seleccionados. Además, durante la semana, el guía envía mensajes, vía WhatsApp o correo electrónico, que contienen tanto consejos como sugerencias sobre la forma de abordar algunos contenidos y la metodología empleada.
A continuación, se presenta uno de estos mensajes de retroalimentación a Lucas:
Como se puede observar en el extracto, el guía sugiere considerar problemas más cercanos a la realidad de los estudiantes (Henríquez-Rivas y Verdugo-Hernández, bajo revisión), a modo de comprometerlos con la clase y generar actividades de dificultad progresiva.
Análisis e interpretación de la sesión
La baja participación de los alumnos lleva al FP a desarrollar por sí mismo todas las tareas presentadas. En el inicio de la clase, Lucas presenta una tarea introductoria (figura 4), en lenguaje natural, que requiere relacionar la determinación del segundo cuartil con el cálculo de porcentajes. Desde la perspectiva del ETM, se busca activar el referencial relativo a los conocimientos previos sobre porcentajes, en relación con el tema presentado (cuartiles), y comenzar el trabajo matemático a partir de la génesis semiótica, debido al uso de la representación numérica de los datos.
En términos de las habilidades (MINEDUC, 2016b), la tarea inicial se planifica para que los estudiantes resuelvan un problema (RP) contextualizado en una red social que ellos usan, sin embargo, la propuesta no logra impactar en su motivación. En este sentido, el ETM previsto en la planificación de Lucas no ocurrió en el ETM implementado, evidenciando una distancia entre ambos. Por su parte, a pesar del contexto cotidiano planteado en esta tarea, son escasos los elementos que permiten señalar que se busca un trabajo de la habilidad de representar, contemplada en lo planificado para la sesión.
Las tareas mostradas están precedidas por la definición de medida de posición y la presentación de la fórmula para determinar la posición de los cuartiles; esta última se expone sin reflexión respecto de su resolución para obtener la fórmula general. Las tareas propuestas en adelante (ETM previsto) pretenden aplicar dicha fórmula y establecer una forma de proceder para determinar los cuartiles, encaminando el trabajo hacia la habilidad de resolver problemas, que en este caso inicia por la aplicación directa de la fórmula en una estructura determinada. En la figura 6, se aprecia la ejemplificación de este procedimiento.
Para motivar la participación de los estudiantes, Lucas intenta generar diálogo con ellos, a través de distintas preguntas, pero no se muestran participativos. Durante la actividad de la figura 6, destacamos una intervención del alumno E3, quien se cuestiona agregar una unidad a 4 (ver figura 11) para determinar la posición de uno de los cuartiles, como se observa en el siguiente extracto.
4 FP: Los cuartiles dividen a una muestra de datos en 4 partes iguales.
5 FP: ¿Qué es una muestra?
6 E3: ¿Por qué se le suma el 1 al 4?
7 FP: Pues no me da un resultado, por lo que a la parte entera (de 4,5) le sumo en 1 y ahí me da la posición 5.
8 FP: Continuamos con el cuartil 2. El cuartil 2 corresponde a la mediana.
9 FP: ¿Por qué relacionamos los porcentajes con cuartiles?, porque se habla de porcentaje en los cuartiles.
Lucas responde a la pregunta del estudiante sin precisar el fundamento de este procedimiento. La respuesta la interpretamos como una focalización del trabajo matemático en la aplicación de la fórmula para determinar cuartiles de forma numérica y algebraica, lo que significa privilegiar la génesis semiótica e instrumental sobre lo discursivo. Asimismo, se observa un rápido regreso a lo calculatorio que demanda la tarea propuesta, cuando señala ''Continuamos con el cuartil 2. El cuartil 2 corresponde a la mediana”.
El trabajo matemático en esta tarea (figura 6), ETM implementado, se restringe a lo numérico, partiendo del referencial con las medidas de posición para activar la génesis semiótica mediante el ordenamiento de los datos. La tarea aborda la habilidad de representar los datos de manera creciente, para conseguir visualizar la posición de los cuartiles solicitados y obtenidos con la ayuda de la aplicación de la fórmula. Esto último nos permite observar el rol de artefacto que Lucas asigna a la fórmula y la activación de la génesis instrumental en el trabajo matemático que promueve en la sesión.
Por su parte, la tarea de la figura 7a es una puesta en práctica del procedimiento recién instaurado (figura 6). Se activa, en su mayor parte, la génesis semiótica, dando sentido a la posición del cuartil por medio del uso del ordenamiento de los datos. Lucas utiliza la fórmula como una herramienta teórica que permite la obtención de los cuartiles, sin generar un cuestionamiento sobre ella, más allá de su uso, restringiendo la aparición de la génesis discursiva en el trabajo propiciado en el aula. Lucas plantea, además, una tarea de las mismas características que la anterior, pero esta vez incluye la construcción del diagrama de caja y bigotes para ubicar y visualizar los cuartiles como medidas de posición. Se observa que el FP pretende activar la génesis semiótica e instrumental, a través de la elaboración del diagrama y el uso de la fórmula.
En términos de las habilidades, el FP retoma la resolución de problemas desde la aplicación de la fórmula para los cuartiles. Al igual que antes, se observa la activación de la génesis semiótica, desde el representamen hacia la visualización, pues la tarea presenta los datos para determinar los cuartiles (figuras 7a y b), trabajados de forma numérica por parte del FP (ETM implementado). En este sentido, se observa el desarrollo de las habilidades de representar y aplicar, sin embargo, esta última no fue explicitada en la planificación (ETM potencial). Tanto en esta como en las siguientes tareas (figuras 8a y b) se observa que Lucas recurre a la visualización para activar el referencial de los estudiantes, mediante la relación entre el cuartil calculado, vía la fórmula y su ubicación en el diagrama de caja y bigotes. Así, el establecer relaciones se transforma en otra habilidad presente en el trabajo matemático de Lucas que no está contemplada en su planificación.
En la actividad de la figura 8a, el FP vuelve sobre la relación entre los cuartiles y el diagrama de caja y bigotes. Aquí no hay una tarea directa para los alumnos, sino que es Lucas quien utiliza esta actividad para explicitar la ubicación de los cuartiles en el diagrama. La habilidad de representar está presente en este trabajo como algo que se espera en los estudiantes, pero que es modelado por el FP. De este modo, la labor matemática propuesta promueve la activación de la génesis semiótica y del polo referencial como foco de esta actividad.
En la tarea de la figura 8b se pide a los aprendices usar el trabajo realizado por Lucas en la actividad anterior. En este caso, al estar determinados los diagramas y cuartiles, se exige establecer una correspondencia entre ellos, la que debe darse entre el registro numérico y el gráfico. Se trata de una labor semiótica, en la cual la activación del referencial permite establecer estas relaciones y dar respuesta a la tarea.
Por su parte, en la fase 6, el profesor guía solicita a Lucas la inclusión de actividades que aborden la construcción de la fórmula y, con ello, que active la génesis discursiva, pues observa que el FP solo se focaliza en el cálculo de cuartiles, lo que, en el sentido del ETM, corresponde a un trabajo semiótico-instrumental. Asimismo, recomienda aumentar la complejidad de las tareas durante la sesión, lo cual interpretamos como conocimiento del guía sobre el desarrollo progresivo de las habilidades que requiere el trabajo matemático en esta asignatura.
Finalmente, en la fase 5, Lucas registra en su bitácora sus reflexiones sobre la enseñanza (figura 12). El FP señala haber logrado el objetivo de que sus estudiantes comprendieran las medidas de posición, sin embargo, esto se restringió al trabajo desde las definiciones de los conceptos, debido al tiempo disponible para la sesión. Además, indica que no pudo desarrollar otras tareas que involucran la resolución de problemas, lo que muestra la conciencia de Lucas sobre las falencias de su planificación y de su clase, pero no las explicita o precisa, como un cuestionamiento crítico de su práctica.
Discusión
En la propuesta de Lucas, en su primera clase, se observan tareas que requieren de representar, aplicar y establecer relaciones, consideradas parte del desarrollo de la habilidad para resolver problemas (RP). El aspecto semiótico del trabajo propuesto muestra la relación entre el objetivo y las habilidades (declaradas en la planificación), incluidas en el diseño del ETM idóneo y del ETM implementado. Sin embargo, una planificación simplificada, como la exigida a Lucas por el centro de práctica, no da cuenta de todas las habilidades que se necesitan, se ven involucradas o se busca desarrollar durante la sesión.
Las habilidades declaradas en el currículo chileno sobre representar, modelar, resolver problemas, así como argumentar y comunicar (MINEDUC, 2016a), a su vez, involucran otras. Por ejemplo, la resolución de problemas involucra identificar, seleccionar, establecer relaciones, aplicar y representar, etc. (Chico, Gamboa y Henríquez, 2017; MINEDUC, 2016b), de acuerdo con el tipo de problema por resolver y las características propias del resolutor, esto es, las características cognitivas del individuo como estructuración del ETM personal (Kuzniak, 2011), traducidas en habilidades propias de la construcción del conocimiento matemático.
Las tareas que potencian la habilidad de RP Lucas las plantea como situaciones en contextos cercanos a los estudiantes (Henríquez-Rivas y Verdugo-Hernández, bajo revisión), en las cuales se debe aplicar un procedimiento y una fórmula previamente establecida, con miras a luego relacionar dos representaciones para los cuartiles. En este sentido, en la RP se involucran otras habilidades, no consideradas explícitamente en el currículo, por ejemplo, las duplas descubrir-explorar, justificar-razonar y presentar-comunicar, que caracterizan el trabajo matemático, según Gómez-Chacón et al. (2016), y que están asociadas a los planos verticales del ETM. El análisis de las tareas matemáticas, a la luz del ETM, permite identificar y caracterizar el trabajo matemático propuesto con ellas, en términos de ''competencias matemáticas cognitivas fundamentadas en la coordinación de las génesis en sus relaciones con el plano epistemológico''(p. 10) que, para nuestro foco de estudio, corresponden a habilidades disciplinares por desarrollar durante la enseñanza de la matemática, pero que no son explícitas en la propuesta ministerial.
En cuanto a las habilidades incluidas en el currículo chileno, cabe preguntarnos por qué se han seleccionado cuatro y no otras como las mencionadas antes. En esta línea, Breda et al. (2016) identifica que son las tendencias ampliadas en investigaciones en educación matemática las que guían los ajustes curriculares y los programas de formación, incluyendo, en dichos ajustes, aquellos temas que actualmente se están desarrollando en la disciplina. En este caso, se identifica una tendencia, por ejemplo, sobre la resolución de problemas (e. g. Pino-Fan, Báez-Huaiquián, Molina-Cabero y Hernández-Arredondo, 2020) y las competencias que se despliegan a través de la modelización (e. g. Trelles, Toalongo y Alsina, 2022), como tópicos de interés en este ámbito de estudio.
El FP, en relación con las tareas propuestas sobre nociones de estadística, privilegia aquellas encaminadas hacia resolución de problemas, mostrando la activación de la génesis semiótica, lo que caracteriza el ETMi. Cabe mencionar que se ha analizado solo la primera clase diseñada por Lucas, en la cual solo ha planificado el desarrollo de la habilidad de representar (o usar representaciones) y que, en ningún momento de su clase ni de su bitácora, mostró conciencia sobre el trabajo con otras habilidades que podrían estar involucradas. Lo anterior da cuenta de la coherencia entre las tareas propuestas (contempladas en el ETMi) y la habilidad objetivo, pero también deja ver la falta de reflexión del FP sobre otras habilidades involucradas en su propuesta de enseñanza.
También se observa la activación del referencial del plano epistemológico, en cuanto a las nociones estadísticas involucradas, pero no se activa el componente de la prueba, por lo que no podemos evidenciar la activación de la génesis discursiva y, por tanto, no hay actividad en los planos (sem-dis) o (ins-dis), alejándose del desarrollo de argumentar y comunicar, como se espera abordar siguiendo las bases curriculares (MINEDUC, 2016a). Asimismo, la génesis instrumental se ve restringida a la aplicación de la fórmula como una herramienta teórica para determinar cuartiles y su posición, sin fomentar otro tipo de trabajo, por ejemplo, la utilización de algún software para el manejo de los datos o la construcción de los diagramas, pues el diagrama de caja y bigotes fue siempre dado por Lucas.
La clase estudiada evidencia una escasa interacción entre el FP y los estudiantes, lo que podría ser atribuido al contexto de clases virtuales (CEM, 2021) a causa de la situación de la pandemia por COVID-19. De acuerdo con Zurita (2020), las intervenciones disminuidas de los alumnos impactan negativamente el desarrollo de las habilidades, mientras que fomentar un contexto de trabajo colaborativo ayudaría a fortalecer las relaciones entre pares e incrementar el desarrollo de habilidades cognitivas. Lucas busca que el grupo contribuya mediante preguntas dirigidas, pero poco estimulantes, y pretende atraer su atención por medio del uso reiterativo de ostensivos (en el sentido de Brousseau, 1998), como colores y formas. El problema contextualizado del inicio de la sesión incluye este tipo de elementos, cercanos a los estudiantes, pero no logra el compromiso necesario para que ellos aborden la tarea. Las siguientes actividades van perdiendo esa cercanía y su presentación se enfoca en desarrollar un procedimiento numérico (cálculo de cuartiles) por encima de la comprensión profunda del tema. Con ello, los alumnos focalizaron la forma en lugar del fondo del tema en estudio, sin cuestionarse, por ejemplo, el desenvolvimiento de la fórmula de cuartiles o su aplicación en otras áreas del conocimiento y en situaciones cercanas a ellos.
Por su parte, el guía recomienda a Lucas que existan tareas cercanas para los estudiantes, tal como señalan Henríquez-Rivas y Verdugo Hernández (en prensa), de modo que los comprometan con el trabajo de la clase, que ellas progresen en su nivel de complejidad y que los alumnos participen activamente de la sesión. La experiencia del guía resulta ser un insumo importante en la formación del FP, pues de ella se obtienen elementos que aportan al desarrollo de propuestas de enseñanza y diseños más sólidos de ETM idóneos.
Conclusiones
La planificación del FP relativa al desarrollo de la habilidad de representar, a través de las actividades recomendadas, parece ocultar otras habilidades matemáticas que serían necesarias para desarrollar las tareas y el trabajo sugerido. Si bien en la propuesta existen tareas que evocan diferentes tipos de habilidades, no resulta explícito que aquellas se seleccionen y organicen para dar el andamiaje a la habilidad de representar, tal como lo sugiere el currículum chileno. El desarrollo de esta habilidad se ve restringido por la baja participación de sus estudiantes en las clases virtuales. Debido a esto, es Lucas quien realiza cada tarea y el trabajo sobre las representaciones, mostrando lo que espera que logren sus estudiantes, en lugar de incentivar que sean ellos mismos quienes las construyan o elijan, es decir, que desarrollen la habilidad.
Coincidimos con Chico et al. (2017) en que son las tareas las que podrían incentivar el desarrollo de las distintas habilidades declaradas en el currículum, así, la selección adecuada de estas, que proyecte su desenvolvimiento y logre comprometer a los alumnos con el trabajo propuesto, se vuelve un asunto importante de considerar como parte del conocimiento profesional del FP, el que debe ser desarrollado durante su formación.
En el caso estudiado, Lucas realiza elecciones de tareas y presenta sus clases enfocadas en mostrar, principalmente, las temáticas estadísticas contempladas en el programa de estudio del nivel (como la fórmula de los cuartiles y su cálculo), en lugar de resaltar las habilidades que deben lograr sus estudiantes. Pareciera ser que Lucas aún no toma conciencia de que, en el ejercicio de su profesión, debe fomentar el trabajo de las cuatro habilidades establecidas en el programa de estudio (MINEDUC, 2016a), como lo exigen los estándares de su formación y desempeño (MINEDUC, 2021). Además, adecuar la planificación al formato exigido por el centro de práctica de Lucas tampoco contribuye a dilucidar la relación entre los objetivos, los contenidos y las habilidades que este propone trabajar, frente a lo cual las orientaciones del guía se tornan un factor importante, al formar y acompañar al FP.
En cuanto al trabajo matemático que fomenta el FP, el ETM idóneo implementado se caracteriza por privilegiar el trabajo semiótico, lo que se alinea con la habilidad declarada en su planificación. Asimismo, se observa la presencia del componente del referencial, por medio del uso de la fórmula para calcular los cuartiles, usada como herramienta teórica en la génesis instrumental. Otros componentes del ETM se ven escasamente activados, restringiendo el tipo de trabajo que se promueve en la sesión. Los aspectos discursivos del trabajo matemático quedan ausentes; son relegados por lo operatorio del cálculo de cuartiles y la interpretación de los diagramas de caja y bigotes. En esta línea, podemos establecer que el trabajo que Lucas incentiva durante la clase, mediante el enfoque tradicional de la enseñanza de la matemática, es principalmente semiótico y operatorio: busca visualizar e interpretar los cuartiles determinados como separadores de una colección de datos.
El trabajo semiótico es natural de la actividad matemática, pero Lucas lo muestra desvinculado con la habilidad de representar que pretende desarrollar. Reconocemos que analizar solo una sesión de clases y su planificación resulta una limitante para caracterizar todo el trabajo matemático del FP y que el estudio del desarrollo de las habilidades debe observarse a largo plazo. Sin embargo, la imagen que resulta de esta primera sesión puede dar cuenta de cómo el FP concibe la enseñanza y la propuesta para desarrollar habilidades, reflejando lo que podrá ser su desempeño docente al egresar como profesor.
Lo anterior nos permite dar respuesta a la pregunta que guio esta investigación sobre el tipo de trabajo que promueve el profesor y el desarrollo de habilidades en una propuesta inicial para la enseñanza de los cuartiles y, junto con ello, nos abre nuevos cuestionamientos respecto del desenvolvimiento y análisis de las prácticas tempranas. Por ejemplo, sobre las características de los profesores guías y su formación como tales, de modo que sean profesionales capaces de acompañar con eficacia a los futuros docentes mediante sus conocimientos y experiencias, pues su participación y las retroalimentaciones ofrecidas a los FP en las instancias de práctica son un aporte a la formación.
Lo anterior nos hace reflexionar sobre la preparación lograda por los futuros profesores hasta su última instancia de práctica, especialmente si las deficiencias observadas en el caso estudiado persisten en el ejercicio de los docentes, una vez completada su formación inicial. De este modo, el FP necesitará desarrollar conocimientos disciplinares, didácticos, técnicos y prácticos, entre los que se encuentran aquellos sobre las diferentes habilidades involucradas en el trabajo matemático que promueve en sus clases, así como tener presentes cuáles son las que permiten potenciar el desenvolvimiento de las contempladas en el currículo. Esto constituye una proyección del presente estudio, por ejemplo, hacia el abordaje de los saberes que los futuros profesores pueden/deben implementar en su formación, respecto del desarrollo de las habilidades disciplinares y sobre la selección de tareas adecuadas para conseguirlas.
Finalmente, es imperativo permanecer vigilantes en la FID, al menos, en las tres direcciones que aquí se mencionaron: el desarrollo de las prácticas, el rol de los profesores guía y tutor y en cómo este contexto permite generar insumos de retroalimentación hacia toda la formación y la investigación en didáctica de la matemática.
Agradecimiento
Paula Verdugo-Hernández agradece el financiamiento a ANID, Proyecto Fondo Nacional de Desarrollo Científico y Tecnológico de Iniciación 2023, folio 11230240, Chile, y al Convenio Marco FID-TAL 1856, de la Universidad de Talca (2021). Gonzalo Espinoza-Vásquez agradece el financiamiento a ANID, Proyecto Fondo Nacional de Desarrollo Científico y Tecnológico de Iniciación 2023, folio 11231088, Chile. Este trabajo está vinculado a la Red MTSK de la Asociación Universitaria Iberoamericana de Posgrado (AUIP).