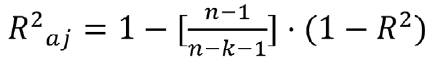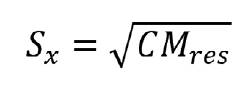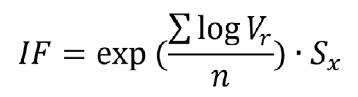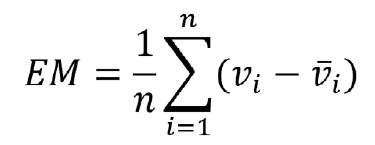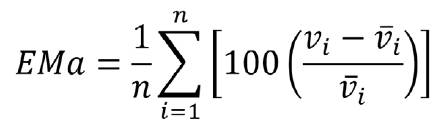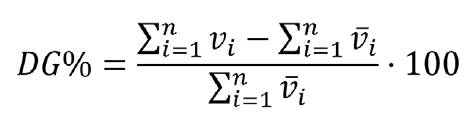Introducción
La necesidad de disponer de una herramienta eficiente que permita obtener valores precisos de la existencia volumétrica de una especie arbórea es de vital importancia para la gestión de las masas forestales. Entre estas herramientas se encuentran los modelos matemáticos llamados ecuaciones volumétricas, que constituyen un procedimiento coherente y eficiente para la cuantificación del volumen de madera de una plantación forestal (1), (9), (18). Un modelo volumétrico es el que describe las relaciones cuantitativas entre el volumen real de madera y las variables dendrométricas medidas directamente en el árbol. En el proceso de explotación industrial la determinación del volumen de madera en pie es un requisito fundamental, principalmente cuando la actividad empresarial está dedicada a una constante producción de madera (4), (8).
Es posible utilizar variables dendrométricas de fácil colecta como el diámetro normal o diámetro a la altura del pecho (d o DAP) y la altura total del árbol, que, asociadas a las ecuaciones volumétricas, permiten estimar el volumen de madera del árbol, a través de ecuaciones matemáticas construidas para la especie y localización en estudio (12). En ese sentido, ecuaciones volumétricas también pueden ser utilizadas para calcular el volumen máximo de madera aserrada que puede obtenerse a partir de madera en rollo (7). Para una determinación rápida de las existencias madereras de un rodal o cuartel, así como para la cubicación de árboles apeados, es posible construir tarifas de cubicación, ecuaciones en las cuales las variables independientes se obtienen de forma sencilla, siendo que la variable dependiente es el volumen de madera. En otro tiempo, las relaciones entre variables medidas directamente (diámetros, alturas) y variables estimadas con ecuaciones (volúmenes) se expresaban por medio de tablas de volúmenes, si bien, desde la introducción de los medios informáticos en el inventario forestal, dichas relaciones se plasman en forma de ecuaciones que serán integradas en las diversas aplicaciones informáticas auxiliares de la gestión forestal.
La literatura registra ecuaciones de volúmenes de madera de una, dos o tres entradas (24), (21). Las tarifas de una sola entrada normalmente estiman el volumen a partir del diámetro normal y se denominan tablas o ecuaciones locales (tarifas de ordenación) y se caracterizan por su aplicación en sitios muy homogéneos. En las ecuaciones de doble entrada, denominadas estándar, generalizadas o tarifas de cubicación, los volúmenes de madera son estimados a partir de dos variables, que pueden ser el diámetro normal (d) y la altura del tronco o del árbol (h). Existen varios modelos, compuestos por una combinación de dos variables independientes (por ejemplo, d2 x h) como si fuese una sola variable. Las ecuaciones de dos entradas son más utilizadas y proporcionan normalmente mayor precisión en la determinación del volumen de madera.
Especial atención se ha dado a la evaluación de los límites de aplicación de las ecuaciones para el volumen, los cuales, por naturaleza, están asociados a las variaciones del efecto del sitio correspondiente (9), (8), (13). Sin embargo, poca atención ha sido dada a la estimación del número mínimo de árboles necesarios para la obtención de ecuaciones para el volumen.
Una especie de eucalipto bastante utilizada en las regiones del centro-oeste y centro-sur brasileño para la producción de madera destinada a obtener celulosa, carbón vegetal y leña es Eucalyptus urophylla S.T. Blake, que presenta facilidad de manejo pudiendo adaptarse a diferentes sitios forestales brasileños e inclusive se registra eficiente crecimiento y productividad en sitios extra tropicales (15), (19).
El objetivo de este trabajo fue ajustar los datos dendrométricos diámetro normal y altura total del árbol a siete ecuaciones volumétricas para una plantación de E. urophylla en edad de cosecha para la producción de leña.
Materiales y métodos
Los datos de campo utilizados para la realización de este trabajo fueron colectados en una plantación de E. urophylla perteneciente a una reforestación industrial localizada en el municipio de Ipameri, Estado de Goiás - Brasil, específicamente en las coordenadas geográficas 16° 11’ 40” S y 47° 19’ 45” W - SAD’69. En la época de la obtención de los datos de campo la plantación se encontraba en la edad de cinco años, precisamente en el punto de cosecha final, destinada exclusivamente para la producción de leña. Se debe mencionar que en esa región el ciclo de corte de rodales con la especie E. urophylla corresponde desde hace más de una década a cinco años de rotación comercial.
En los cuarteles destinados al corte raso fueron seleccionados aleatoriamente 11 rodales y en cada uno de ellos se estableció una parcela de 20 x 50 m. Con un espaciamiento de 3 x 2 m fueron encontrados aproximadamente 150 árboles por parcela, distribuidos en 6 hileras de 25 árboles. Las variables dendrométricas colectadas fueron diámetro normal y altura total de 1545 árboles en pie de E. urophylla. El (d), en centímetros, fue medido con una forcípula de 80 cm de brazo y la altura total, en metros, fue determinado por medio de un hipsómetro Haga en la escala de 20 m. Todos los árboles con (d) igual o superior a 5 cm fueron medidos, por tanto, el diámetro mínimo considerado fue de 5 cm. No se encontró ningún árbol en pie que tuviese un (d) inferior al mínimo considerado. El derribo de los árboles se efectuó con motosierra a 0,30 m de altura, siendo que la primera troza de un metro de longitud alcanzó la altura de 1,30 m, correspondiendo al diámetro normal.
Una vez apeado el árbol se procedió a la cubicación, seccionando cada árbol en trozas de 1 m de altura, hasta llegar a la troza de la punta de la copa. En cada troza de 1 m se realizó las medidas de los diámetros extremos con corteza. Para el cálculo del volumen de cada troza se utilizó la ecuación de Smalian (10). La altura o longitud de la última troza del tronco, denominada troza de la punta de la copa quedó definida hasta donde existía el diámetro mínimo de 5 cm. El volumen de esa troza fue calculado por la fórmula de Huber. La sumatoria del valor del volumen correspondiente de cada troza incluyendo el de la troza de la punta de la copa proporcionó el volumen real del árbol.
Se seleccionaron siete modelos que consideran únicamente una variable dendrométrica, denominadas ecuaciones de una entrada (tarifas de ordenación), y nueve ecuaciones volumétricas de dos entradas (tarifas de cubicación), extraídas de (14). Las 16 ecuaciones volumétricas escogidas (Cuadro 1) se efectuaron a través del programa SAS, los siguientes cálculos con la finalidad de identificar el mejor ajuste: coeficiente de determinación ajustado (R2 aj), raíz del error medio cuadrático, también conocido como error padrón de la estimación (Sx), gráfico de residuos y el índice de Furnival (IF) (3), (5), (20), (22), (27), (28).
El coeficiente de determinación ajustado (R2aj) fue obtenido por la expresión (1):
donde: k es el número de variables independientes
n es número de observaciones de la muestra
El error padrón de la estimación (Sx) se determinó por la ecuación (2):
donde: CMres es el cuadrado medio del residuo obtenido del análisis de la varianza.
El Índice de Furnival (IF) se calculó por la expresión matemática (5) (3):
donde: Vr es volumen individual real en m3
sx es error padrón de la estimación
La selección de la ecuación se fundamentó en el mayor coeficiente de determinación ajustado presentado, menor error padrón de la estimación (2), (25), (26) y menor valor del índice de Furnival (28). Estos estadísticos de ajuste fueron ordenados en puntajes de jerarquía (rank) para permitir una selección objetiva y concluyente de las ecuaciones.
La selección del modelo volumétrico siguió el proceso de validación a fin de asegurar que los resultados puedan ser generalizados a la población en cuestión (21) y que no fuesen específicos de la muestra utilizada para la correspondiente estimación (20). Para el análisis de validación cruzada fueron considerados 310 árboles (20 % del total de la población) correspondiendo a los datos de prueba independientes. La validación utilizada en este trabajo consideró las técnicas estadísticas del análisis de residuos entre los valores estimados por el modelo y los datos medidos para su construcción. La calidad de la estimación fue calculada conforme (21):
Error medio absoluto (EM) (3)
Nivel de confianza del 95 %, con un error de muestreo máximo de 10 % (4).
Error medio absoluto (EMa) en valor porcentual (%) (5),
donde: vi es volumen individual de cada árbol en la muestra
vi =es el volumen medio estimado del árbol en la parcela
n es el número de árboles.
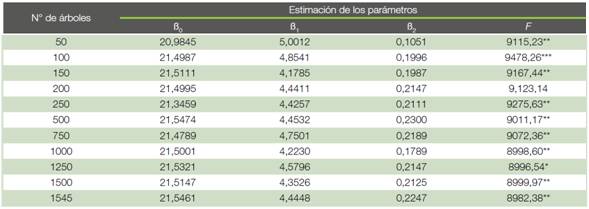
A partir de la ecuación seleccionada, con la finalidad de obtener el mínimo tamaño muestral n necesario para lograr un ajuste suficientemente preciso, se ajustó la ecuación para muestras de árboles crecientes, desde 50 árboles escogidos al azar hasta llegar en conjuntos de 25 individuos a los 1545 árboles. En cada conjunto de datos se calculó el valor de F de Snedecor y el nivel de significación del análisis de la varianza.
Resultados y discusión
En el Cuadro 2 se muestran los parámetros estadísticos que definieron la precisión del ajuste de las ecuaciones analizadas. El análisis de precisión realizado, considerando el coeficiente de determinación ajustado, el error padrón de la estimación y la distribución de los residuos corrobora con los procedimientos efectuados en forma similar en los trabajos de (4), (16), (23). Los modelos desarrollados en función de las variables dendrométricas diámetro normal y altura total respondieron satisfactoriamente cuando se aplicaron las transformaciones logarítmicas de las variables (modelos 5, 6, 15 y 16). La comparación de los modelos logarítmicos con los modelos lineales fue determinada por el error padrón de la estimación por medio del factor de corrección de Meyer (FM = e0,5 CMerror).
Tabla 1 Ecuaciones volumétricas evaluadas. v: volumen con corteza; d: diámetro normal; h: altura total; ß0 ß1 a ß5: parámetros del modelo, g: área basal.
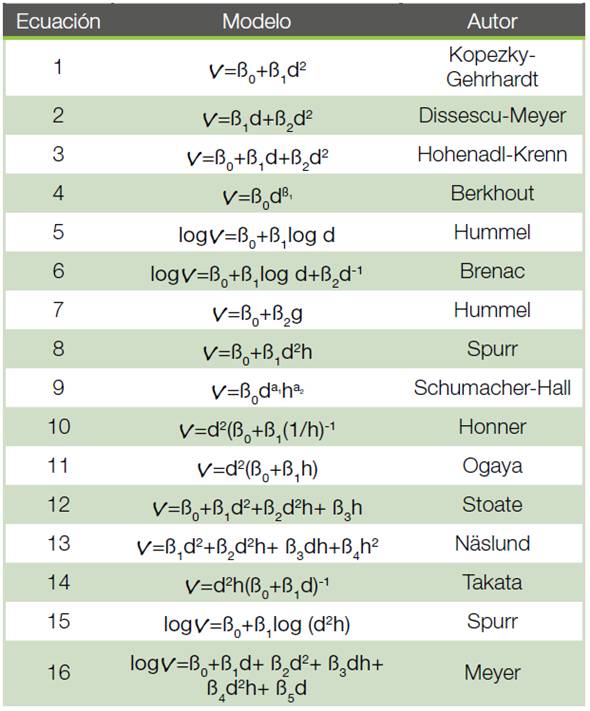
Las 16 ecuaciones analizadas mostraron relativamente buen desempeño estadístico en cuanto a los valores calculados del coeficiente de determinación ajustado (R2 aj), que varió de 0,59 a 0,98 (Hohenadl-Krenn). En nueve modelos los valores correspondientes fluctuaron entre 0,70 y 0,81, mostrando significativo grado de confianza estadística.
Con relación al error padrón de la estimación (Sx) las ecuaciones analizadas presentaron valores bastante bajos entre 0,01 y 0,78, significando que los modelos fueron suficientemente precisos al describir el comportamiento de las variables observadas. La ecuación de Hohenadl-Krenn tuvo un valor de 0,06 (6 %) el segundo inferior en la localización de la lista, por tanto, muy preciso en cuanto a fiabilidad estadística. El índice de Furnival (IF) también se presentó con valores menores a 1, de 001 a 0,77, mostrando así que las estimaciones de volumen con las ecuaciones ensayadas y las variables medidas fueron suficientemente precisas.
Cuadro 2 Modelos de simple entrada de datos (ecuaciones de 1 al 7) y de dos entradas (ecuaciones 8 al 16) con las medidas de bondad del ajuste (R2 aj = coeficiente de determinación ajustado, Sx = error padrón de la estimación, IF = índice de Furnival) y correspondiente orden jerárquico (e.j.)
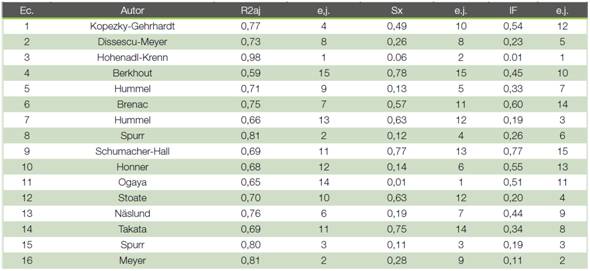
El análisis del orden jerárquico de los modelos ensayados, en función de los estadísticos de bondad de la estimación, identificó que el modelo lineal de Hohenadl-Krenn (ecuación 3) era el más preciso ya que acumuló cuatro puntos en la puntuación jerárquica (sumatoria de los valores correspondientes), seguida por la ecuación 9 (Schumacher-Hall) que tuvo nueve puntos, más del doble que la anterior. Las demás ecuaciones mostraron una puntuación superior a los 20 puntos. En un trabajo realizado en la región cálida húmeda del municipio de Haimanguillo, México con la especie Eucalyptus urophylla, de seis modelos probados, la ecuación de Schumacher-Hall y la de Spurr se presentaron como los mejores modelos de estimación volumétrica (9).
El modelo de Hohenadl-Krenn (ecuación 3) presentó el mayor R2 aj y los menores valores de Sx así como de IF, presentando una buena estimación de la población observada. Este modelo también se caracterizó por su simplicidad al considerar solamente el diámetro normal en dos variables explicativas (d y d2). La correspondiente ecuación matemática ajustada para los datos estudiados resultó ser:
El análisis de la varianza confirmó la calidad del ajuste para la ecuación de Hohenadl-Krenn, mostrando una alta significación estadística (p-valor < 0,0001) entre la variable independiente (d) y la variable dependiente (volumen).
Al realizar la verificación de los presupuestos de la regresión mediante un análisis gráfico de los residuos (Figura 1) se observó una distribución homogénea en ambos lados y a lo largo de la línea horizontal de residuo cero, situación que anima a pensar que los residuos de las estimaciones cumplen con los requisitos de normalidad y homogeneidad de la varianza para realizar el correspondiente análisis de regresión.
Las calidades de las estimaciones obtenidas mediante el proceso de validación fueron de EM = 0,048; Ema % = 8,57 y DG = 6,99. Como se observa, los errores absolutos fueron bajos y el desvío global fue menor que 10 %, satisfaciendo de esta forma plenamente los requerimientos del análisis realizado, una vez que aporta a la acuidad en las estimaciones del volumen total, como objetivo de este estudio.
Figure 1. Average residues distribution (axis x = dependent variable = estimated volume).
Con los resultados referentes a la aplicación en el ANOVA de la regresión de la ecuación de Hohenadl-Krenn (Cuadro 3) se verifica una nítida tendencia decreciente en los valores calculados de F a medida que aumenta el número de árboles usados para el ajuste de los modelos. Se constató que con una mayor colecta de datos disminuye el nivel de significación del modelo ajustado sin que fuese diferido estadísticamente. Por ello, se estima que de 50 a 100 tríos de datos (diámetro normal, altura total, volumen con corteza) sería suficiente para el ajuste de una ecuación de cubicación en este tipo de plantación.
Conclusiones
El procedimiento tecnológico utilizado permitió obtener e interpretar los parámetros estadísticos coeficiente de determinación ajustado, error padrón de la estimación, gráfico de residuos e índice de Furnival, a partir de los cuales fue seleccionado el modelo volumétrico que mejor se ajustaba a los datos colectados en la plantación de E. urophylla.
Para rodales plantados con la especie E. urophylla en la edad de corte raso que corresponde a la edad de cinco años, la ecuación volumétrica de Hohenadl-Krenn, puede ser empleada de forma eficiente y fiable en las correspondientes estimativas de la determinación del volumen maderero y en planes de ordenación forestal de la región estudiada.
La colecta de un número excesivo de datos no significó que la ecuación tuviese mejor ajuste. Datos dendrométricos de 50 a 100 árboles parece ser plenamente aceptable para el n muestral para estimar el correspondiente volumen maderero de plantaciones de E. urophylla en la región de Ipameri, Goiás.