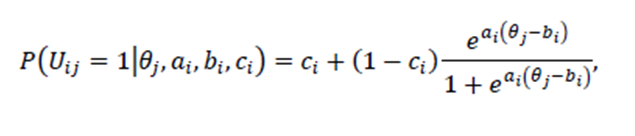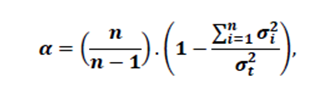Introdução
Criado em 1998, o Exame Nacional do Ensino Médio (ENEM) é uma avaliação estandardizada aplicada anualmente pelo Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (INEP), autarquia federal vinculada ao Ministério da Educação do Brasil (MEC). Seu surgimento se deu da necessidade de avaliar o aprendizado de estudantes do Ensino Médio em todo o país, assumindo um papel de condutor de política pública em prol da qualidade da educação básica em âmbito nacional (Brasil, 1998).
Entretanto, com a consolidação do exame, outras atribuições foram a ele incorporadas, especificamente para selecionar estudantes a serem atendidos em programas sociais de acesso à educação superior, desenvolvidos pelo governo brasileiro. O primeiro desses programas a incorporar os resultados do ENEM foi o Programa Universidade para Todos (ProUni), lançado por Medida Provisória (n° 213/2004), em 2004, e transformado em Lei no ano seguinte (n° 11096/2005). O ProUni tem como finalidade a concessão de bolsas de estudos (integrais e parciais) em universidades privadas (Brasil, 2005).
Ademais, desde 2010 os resultados do exame são utilizados como critério para financiamento de cursos superiores em universidades privadas brasileiras, mediante o Fundo de Financiamento ao Estudante do Ensino Superior (FIES), programa instituído pela Lei nº 10260, de 12 de julho de 2001 (Brasil, 2001).
Contudo, foi a partir de 2009, com a criação do Sistema de Seleção Unificada (Sisu) que o ENEM se consolidou como o maior exame de seleção para o Ensino Superior do Brasil. O Sisu é uma plataforma digital pela qual as instituições públicas de Ensino Superior oferecem vagas aos candidatos que se submeteram ao exame (Brasil, 2009a). Na edição de 2019, que considera os resultados do ENEM 2018, o processo seletivo do Sisu ofertou 235461 vagas em 129 instituições em todo o país (Perez, 2019).
A expansão e a extensão do exame, bem como as atribuições a ele investidas, ao longo dos anos tornam indispensáveis os estudos voltados a avaliar a estrutura e a qualidade desta avaliação (meta-avaliação)1. Entretanto, conforme salientam Sousa, Pontes Junior e Braga (2020) essas características “são pouco exploradas nos estudos e pesquisas em avaliação educacional” (p.3), constituindo um campo vasto e promissor para pesquisadores. Dentre os artigos que atendem a este objetivo, destacamos quatro que se apropriam das técnicas psicométricas para a meta-avaliação do exame.
O estudo de Travitzki (2017) propôs a analisar as provas de 2009 e 2011 do ENEM, por meio de duas vertentes da Psicometria: a Teoria Clássica dos Testes (TCT) e a Teoria de Resposta ao Item (TRI). Os resultados indicaram uma prova com qualidade adequada em 2011, mas duvidosa em 2009, ano em que a confiabilidade da prova se mostrou abaixo dos limites considerados aceitáveis para o coeficiente Alpha de Cronbach (α<0.6). Também foi observado que 25% dos itens de 2009 e 17% dos itens de 2011 apresentam comportamento empírico fora do esperado, segundo o indicador global definido no estudo que considerou: 1) se o item estava suficientemente relacionado ao restante da prova; 2) se a alternativa correta atraiu os respondentes com maior proficiência; 3) se o item discriminou bem no seu nível de proficiência e 4) se foi possível ajustar um bom modelo da TRI para os itens (Travitzki, 2017, p. 270).
O estudo de Lopes, Rubini, Massunaga e Barroso (2015) é mais específico e considera apenas os itens de Física, presentes no ENEM de 2009 a 2012. Por outro lado, além da análise psicométrica foi realizada também uma análise qualitativa, especificamente no que se refere aos descritores e distratores dos itens. Como resultados, perceberam que o desempenho na prova de Física, em que todos os itens foram classificados como difíceis sob a ótica da TRI, foi consideravelmente inferior ao das demais disciplinas da área de Ciências da Natureza e propuseram uma reflexão acerca das dificuldades enfrentadas no processo de ensino-aprendizagem de Física no contexto do Ensino Médio brasileiro. Ademais, os autores destacaram o grande número de itens relacionados a conteúdos pouco abordados ou abordados rapidamente ao final do Ensino Médio, o que poderia explicar o mal desempenho dos estudantes na prova analisada, embora reconheçam a necessidade de se ampliar essas discussões.
Sousa et al. (2020) também partem de uma análise mais específica da prova e consideram os itens de Educação Física do exame presentes nas edições de 2009 a 2014. Em uma abordagem que se apropriou da Psicometria Clássica, sobretudo da Teoria Clássica dos Testes (TCT), concluíram que a prova de 2014 não apresentou unidimensionalidade. Nesse mesmo ano, os itens analisados apresentaram alta dificuldade, baixa discriminação e problemas quanto a fidedignidade, que podem comprometer a validação de seus resultados. Para os demais anos, em geral, os itens apresentaram valores adequados para estes indicadores.
O estudo de Toffoli (2019), por sua vez, considera os itens da prova de Matemática do ENEM 2015. A autora classifica como adequados itens com: 1) coeficiente bisserial de, no mínimo, 0.15; 2) Coeficiente de discriminação entre 0.7 e 2.5 e coeficiente de dificuldade de, no máximo, 3.0, a partir da aplicação do modelo logístico de três parâmetros da TRI; e 3) itens no qual a alternativa correta do gabarito da prova coincidisse com a alternativa considerada correta indicada pelo Modelo de Resposta Nominal (MRN), também da TRI. Como resultados, a autora identificou 26 itens fora dos padrões considerados como adequados e constatou que a prova analisada possui qualidade muito aquém do desejável.
Nessa vertente, este artigo tem o objetivo de analisar a qualidade psicométrica da prova de Matemática da edição de 2018 do ENEM/Brasil. O interesse, assim, é responder à seguinte questão: Os itens que compõem essa prova apresentam parâmetros psicométricos satisfatórios, no que se refere a discriminação e dificuldade dos seus itens e a confiabilidade de seus resultados? Para tanto, realiza-se uma meta-avaliação do exame, mediante a aplicação de técnicas psicométricas a uma amostra de 68438 respondentes, matriculados no 3º ano do Ensino Médio no ano de sua aplicação.
A partir disso, o estudo permitirá avaliar a estrutura dessa avaliação e a confiabilidade dos resultados obtidos. Tal análise se justifica considerando a importância do exame no cenário educacional brasileiro, que torna necessária a utilização de um instrumento confiável para garantir a isonomia entre os seus participantes.
Dessa forma, além desta introdução, o texto está estruturado em outras quatro seções. Na primeira, apresenta-se um breve referencial teórico sobre o ENEM e sobre como a TRI está presente em sua operacionalização. Em seguida, são detalhados os materiais e métodos utilizados e os principais resultados obtidos na meta-avaliação. O artigo se encerra com conclusões obtidas.
2. Referencial Teórico
Nesta seção, inicialmente apresentam-se algumas considerações sobre o ENEM e, em seguida, regatam-se alguns conceitos da Psicometria Moderna, sob a ótica da TRI. Também são apresentados alguns critérios dispostos na literatura, para a análise da qualidade de itens, considerando as técnicas psicométricas, e é discutido o conceito de confiabilidade de um teste, através do uso do coeficiente Alpha, introduzido por Cronbach (1951) e pertencente à abordagem Clássica da Psicometria.
Algumas considerações sobre o Exame Nacional do Ensino Médio (ENEM)
O ENEM é constituído por uma redação e 180 itens objetivos, distribuídos em quatro áreas do conhecimento (Matemática e suas Tecnologias, Ciências da Natureza e suas Tecnologias, Ciências Humanas e suas Tecnologias e Linguagens, Códigos e suas Tecnologias), (Brasil, 2012). Essas áreas possuem uma Matriz de Referência2 que descreve os eixos cognitivos, competências e habilidades exigidas pelos indivíduos que realizam o exame, listando o conteúdo programático do ENEM (Brasil, 2009b).
Os eixos cognitivos são comuns a todas as áreas de conhecimento: dominar linguagens, compreender fenômenos, enfrentar situações-problema, construir argumentação e elaborar propostas (Brasil, 2009b). Por sua vez, as competências e as habilidades demonstram um conjunto de saberes e conhecimentos utilizados como norteadores da aprendizagem dos estudantes e de sua avaliação (Rabelo, 2013).
A construção e análise dos itens da prova, bem como o cálculo da proficiência do estudante, são realizadas com base na TRI, metodologia de avaliação pautada em modelos estatístico-matemáticos. A TRI fornece instrumentos valiosos para a meta-avaliação e foi utilizada, neste artigo, para analisar os 45 itens da prova de Matemática e suas Tecnologias do ENEM 2018, cujos microdados disponibilizados pelo INEP/MEC eram os mais recentes no momento em que esta pesquisa foi realizada.
Teoria de Resposta ao Item
Segundo Pasquali (2009), a TRI foi elaborada por Lord (1952) e Rasch (1960) e axiomatizada por Birnbaum (1968). Entretanto, de acordo com Pasquali e Primi (2003), suas raízes remontam à década de 1930, tendo como precursores os trabalhos de Richardson (1936), Lawley (1943, 1944) e Tucker (1946). Trata-se de “uma reunião de modelos estatísticos usados para fazer predições, estimativas ou inferências sobre as habilidades (ou competências) medidas em um teste” ( Rocha Junior, 2018, p. 17).
Antes de sua difusão enquanto metodologia de análise e estimação de proficiências, predominava nos campos de avaliação a Teoria Clássica dos Testes (TCT) que, em resumo, se propunha a avaliar um conjunto de itens coletivamente, considerando que o número de acertos em uma prova era diretamente proporcional ao conhecimento do respondente. A principal vantagem desta teoria é a praticidade, pois não exige pressupostos rigorosos e pode ser aplicada em diferentes contextos (Costa, Lima e Soares, 2020; Pasquali, 2018; Soares, 2018).
Entretanto, algumas limitações da TCT como o não-controle de acertos casuais ou as dificuldades existentes em processos de comparação entre estudantes submetidos a provas ou edições distintas de um mesmo exame (necessários, por exemplo, para avaliar a eficiência de uma política pública adotada), corroboraram para o surgimento e aprimoramento da TRI. A principal novidade que esta metodologia trouxe foi considerar cada questão da prova como unidade básica para as análises estatísticas, desenvolvendo um conceito de escala de proficiência que traz grandes benefícios para as análises de avaliações (Pasquali, 2018; Rabelo, 2013).
Atualmente a TRI é amplamente utilizada nas avaliações em larga escala em todo o mundo como, por exemplo, no Programme for International Student Assessment (PISA) e no Test of English as a Foreign Language (Toefl). No Brasil, a primeira aplicação da TRI se deu em 1995, através do Sistema de Avaliação da Educação Básica (Saeb). Em seguida, foi implementada no Exame Nacional para Certificação de Competências de Jovens e Adultos (ENCCEJA), na Prova Brasil e, então, no ENEM (Rabelo, 2013).
A TRI se baseia em duas pressuposições principais, que se referem as características dos itens: unidimensionalidade e independência local. O primeiro se refere à existência de uma habilidade dominante, que responde por todos os itens do teste. O segundo, assume que as respostas à diferentes itens no teste ocorrem de forma independente, ou seja, o desempenho em um item não interfere em outro (Andrade, Tavares e Valle, 2000; Pasquali, 2018; Soares, 2018). Hambleton, Swaminathan e Rogers (1991, p. 11) postulam que a “unidimensionalidade implica em independência local”, sendo este pressuposto suficiente para garantir a aplicabilidade da TRI.
Os modelos de TRI comumente utilizados são os modelos logísticos, que permitem um melhor tratamento estatístico e são mais frequentes na literatura da área. Assim, a TRI considera os modelos logísticos de um, dois ou três parâmetros. O modelo logístico de um parâmetro (ML1P) considera apenas a dificuldade do item. O modelo logístico de dois parâmetros (ML2P) considera a dificuldade e a discriminação do item, definida como a capacidade que ele possui para diferenciar respondentes com níveis distintos de conhecimento. Já no modelo logístico de três parâmetros (ML3P) são consideradas a dificuldade, a discriminação e a probabilidade de acerto do item pela casualidade (ou chute) (Andrade, Tavares e Valle, 2000; Pasquali, 2018; Soares, 2018). O ENEM utiliza o ML3P (Brasil, 2009a). Este modelo, proposto por Birnbaum (1968), é expresso matematicamente pela equação:
em que 𝑃 𝑈 𝑖𝑗 =1 𝜃 𝑗 , 𝑎 𝑖 , 𝑏 𝑖 , 𝑐 𝑖 é a probabilidade do indivíduo 𝑗 com habilidade 𝜃 𝑗 acertar o item 𝑖, 𝑎 𝑖 é o parâmetro de discriminação, 𝑏 𝑖 é o parâmetro de dificuldade e 𝑐 𝑖 é a probabilidade de acerto ao acaso do item 𝑖. O ML2P pode ser obtido fazendo 𝑐 𝑖 =0 e o ML1P fazendo 𝑐 𝑖 =0 e 𝑎 𝑖 =1.
A função matemática do modelo, que associa a probabilidade de acerto de um item com seus parâmetros e com a habilidade do respondente, gera uma curva monótona crescente, denominada curva característica do item (CCI). Além da CCI, uma outra medida frequentemente utilizada na TRI é a Curva de Informação do Item (CII) que permite quantificar a precisão com que se pode estimar o nível de conhecimento de um indivíduo por meio da resposta dada por ele ao item, sendo um instrumento eficaz para descrever e selecionar itens de qualidade (Andrade, Tavares e Valle, 2000). Segundo Pasquali (2018), as maiores informações sobre os respondentes são trazidas para aqueles cuja habilidade se encontra em torno do índice de dificuldade do item.
A qualidade do ajustamento dos modelos da TRI é tradicionalmente verificada, segundo Lenhard (2013), pelo teste Qui-Quadrado 𝜒 2 e suas variações, desenvolvidas por Bock (1972) e Yen (1981). A estatística 𝜒 2 permite definir uma região crítica para o teste, que auxilia nestas análises. Desta forma, rejeitamos a hipótese de um bom ajustamento aos dados, quando esta estatística é superior ao valor crítico adotado 𝜒 𝛼 2 .
2.3 Critérios para avaliação da Qualidade dos Itens
Segundo Travitzki (2017, p. 264), os métodos de triagem de itens que incluem análises da dificuldade e discriminação são fundamentais para a meta-avaliação, “pois permitem avaliar a qualidade dos itens por seu comportamento empírico”.
Quanto ao índice de discriminação, de acordo com Baker (2001) e Bortolotti e Andrade (2007) são considerados itens de boa qualidade aqueles que possuem valor acima de 0.65. Para avaliar a dificuldade, a abordagem clássica da psicometria assume o percentual de acerto de cada item. Neste caso, quanto maior este percentual, mais fácil ele é. Entretanto, sob esta ótica, a classificação de um item quanto ao índice de dificuldade vai de acordo com o grupo de indivíduos em que o item foi examinado. Assim, um mesmo item pode ser classificado como fácil para um certo grupo com altas habilidades e difícil para um outro grupo com habilidades menores (Costa, Lima e Soares, 2020; Soares, 2018).
Na TRI, por sua vez, “o cálculo dos parâmetros dos itens independe da amostra de sujeitos utilizada durante o processo de calibração dos itens” (Hambleton e Zaal, 2013, p. 8, [tradução nossa]), constituindo uma das vantagens da adoção desta metodologia em avaliações. Sob a ótica da TRI, o índice de dificuldade (bem como a habilidade do respondente) segue uma distribuição normal padronizada. Neste caso, este índice representa, em módulo, o número de desvios-padrão da média.
Embora varie entre −∞ e ∞, “é usual que os valores encontrados para o índice de dificuldade estejam entre −3.0 e 3.0, teoricamente representando 99.73% do conjunto” (Xie, Davidson, Li e Ko, 2019, p.702, [tradução nossa]). Dessa forma, conforme Vendramini e Dias (2005, p.207) “se 𝑏= −3.0 o item é extremamente fácil, se 𝑏=0.0 o item possui dificuldade média e se 𝑏=3.0 o item é extremamente difícil”.
Para o parâmetro c, que indica a probabilidade de acerto do item pela casualidade, espera-se valores que se aproximam do inverso do número de alternativas disponíveis para serem assinaladas (Hambleton et al., 1991; Pasquali, 2003). No caso dos itens do ENEM, que contam com 5 alternativas de resposta, é esperado valores próximos à 0.2 (1/5) para este parâmetro.
Para uma análise psicométrica global, não há um critério consensual na literatura para a avaliação da qualidade de um teste. Vendramini e Dias (2005), por exemplo, consideram adequados testes com itens que possuem parâmetros 𝑎>0.30; 𝑏 <2.95 e 𝑐<0.40, além de “coeficientes de correlação ponto-Bisserial3 para a alternativa correta superior às demais, em cada item do teste e resíduos padronizados do ajuste do modelo inferiores a 2.0” (Vendramini e Dias, 2005, p.207).
Neste artigo, foram utilizados os critérios adotados por Alnabhan e Harwell (2001), que se baseiam em limites utilizados por Muthén, Kao e Burstein (1991) e consideram adequados testes compostos por itens com um bom ajuste no modelo TRI, percentual de acerto inferior a 90% e cujos parâmetros de discriminação e dificuldade pertencem aos intervalos: 𝑎>0.5 e 𝑏 <3.0, respectivamente.
2.4 Confiabilidade do teste
A confiabilidade de um teste, também denominada fidedignidade, representa a “capacidade em reproduzir um resultado de forma consistente, no tempo e no espaço” (Souza, Alexandre e Guirardello, 2017, p. 650). Em outras palavras, a confiabilidade pode ser interpretada como a capacidade do teste reproduzir resultados semelhantes, quando aplicado ou avaliado por pesquisadores e/ou em momentos distintos, se configurando como um dos principais instrumentos para avaliar a qualidade de um teste.
Dessa forma, a confiabilidade apresenta aspectos que permitem avaliar a consistência interna, a coerência e a precisão do teste. Um dos indicadores de confiabilidade mais utilizados na literatura é o Coeficiente Alpha de Cronbach, cujo nome se deu em homenagem a seu mentor Lee J. Cronbach em 1951. Para calculá-lo, aplica-se a fórmula:
em que 𝑛 é o número total de itens, σ i 2 é a variância relacionada a cada item do teste, e o σ t 2 é a variância da nota dos respondentes do teste.
Embora sua interpretação seja subjetiva, são esperados valores entre 0 e 1, sendo que, teoricamente, quanto mais próximo de 1, mais confiável é o teste. Entretanto, valores acima de 0.9 podem indicar a presença de itens redundantes ou duplicações (Streiner, 2003).
Quanto ao valor mínimo considerado satisfatório para este indicador, há uma discussão na literatura especializada. Alguns autores como Meliá (1990) e Nunnally (1978) assumem ser necessário um coeficiente acima de 0.7 para garantir a confiabilidade do teste. Outros autores como DeVellis (1991) e Hair Jr., Black, Anderson e Tatham (2005), defendem que um valor acima de 0.6 já é considerado satisfatório.
Metodologia
3.1 Enfoque
Este artigo apresenta os resultados de um estudo empírico de caráter quantitativo e exploratório, que utilizou como fonte os microdados do ENEM/Brasil em 2018, sendo estes os mais recentes disponibilizados pelo INEP/MEC no momento em que esta pesquisa foi realizada.
3.2 Unidades de análise
Para compor a amostra que foi analisada, inicialmente selecionou-se, ao acaso, 1 milhão de participantes do ENEM/Brasil em 2018. Como se tratou de um exame aberto à participação de qualquer cidadão, optou-se por analisar apenas os estudantes que cursavam e concluiriam o Ensino Médio em 2018, correspondendo a um total de 318801 participantes, reduzidos a 274919 com a exclusão dos que apresentavam dados ausentes (NA’s). Por fim, devido à divergência nos gabaritos dos modelos de cadernos de prova4, considerou-se apenas os participantes que responderam à prova de matemática do caderno azul da primeira aplicação (código 459), restando um total de 68438 participantes para o ensaio.
3.3 Técnicas de coleta de dados
Os microdados do ENEM são disponibilizados de forma detalhada pelo INEP/MEC no formato Comma-separated values (CSV). Além dos documentos técnicos, esses microdados contêm os questionários socioeconômicos, aplicados junto às provas, que permitem ampla variedade de pesquisas educacionais, demonstrando o primor do órgão pela transparência dos resultados. Contudo, nas análises deste artigo, de caráter descritivas, considerou-se apenas a prova, os gabaritos e as informações sobre os itens de Matemática do ENEM 2018.
Embora o INEP/MEC seja conservador em divulgar alguns procedimentos metodológicos que envolvem o ENEM, sabe-se que é utilizado um modelo logístico de 3 parâmetros, que também será o modelo considerado para se estimar os parâmetros dos itens e dos respondentes que compõe a amostra analisada neste estudo. Segundo Pasquali (2003, p. 92), “este processo de estimação se faz por aproximações sucessivas (iterações)”.
3.4 Análises dos dados
Para a análise dos microdados do ENEM 2018, optou-se pelo uso do software estatístico R (R Core Team, 2020), versão 3.6.2. Este software, livre e de código aberto de fácil manuseio, oferece uma ampla variedade de análises estatísticas. Todas as análises foram realizadas utilizando o pacote ltm (Rizopoulos, 2006) deste software.
A estimação dos parâmetros dos itens e da proficiência dos respondentes se deu considerando 61 pontos de quadratura, 1000 iterações quase-Newton e 400 iterações Estimation-Maximization. De acordo com Travitzki (2017), essas configurações, acompanhadas de uma amostra de no mínimo 30 mil provas, normalmente são suficientes para uma boa calibração dos itens.
Para a calibração dos itens foi desenvolvida uma Escala de Proficiência considerando o ENEM 2018 como referência. Dessa forma, ressalta-se que os parâmetros dos itens estimados neste estudo não são, necessariamente, os utilizados no ENEM, cuja calibração se faz utilizando a escala do ENEM 2009, ano da primeira aplicação da TRI no exame. Essa escala considera que a proficiência média dos respondentes corresponde a 500 pontos, com desvio-padrão de 100 pontos (Brasil, 2012).
Para avaliar o pressuposto da unidimensionalidade, considerou-se o segundo autovalor da matriz de correlações tetracórica dos itens dicotômicos ( 𝜆 2 ) e a média dos segundos autovalores obtidos por simulação de Monte Carlo ( 𝜆 ), pautando-se na metodologia proposta por Drasgow e Lissak (1983), conhecida como análise paralela modificada. Em síntese, essa metodologia procura determinar quando as violações a esse pressuposto são tão graves que não permitem estimar os parâmetros do modelo da TRI de forma satisfatória. O software R retorna um p-valor, baseado nesse procedimento, que nos permite concluir se a hipótese de unidimensionalidade ( 𝐻 0 ) é aceitável ou não.
A qualidade do ajuste do modelo foi analisada pelo teste Qui-Quadrado de Bock (1972), pela qual a estatística é obtida pela comparação entre o valor observado, obtido pela frequência de resposta em cada intervalo de habilidades, e o valor esperado, mensurado utilizando a estimativa dos parâmetros dos itens e a mediana estimada nesses intervalos. Assumiu-se a divisão das habilidades em 10 subgrupos com amplitudes iguais (𝐺=10) e adotou-se, para os testes de hipóteses citados, 5% como nível de significância.
Para os itens bem ajustados, inicialmente são apresentados os parâmetros psicométricos estimados, a porcentagem de acerto e a habilidade com a qual se relacionam. Essas medidas foram úteis para avaliar a qualidade do teste e dos itens que o compõe. Em seguida, apresenta-se o item com maior parâmetro de discriminação e suas curvas característica e de informação, visando ilustrar, mais detalhadamente, o funcionamento das técnicas da TRI.
Com o intuito de verificar como se dá a relação entre o número de acerto no teste e a proficiência do estudante, estimada via TRI, também são apresentados alguns gráficos que tratam dessas variáveis. A análise da confiabilidade do teste foi realizada pelo Coeficiente Alpha de Cronbach. Visando um resultado mais conservador, adotou-se como referência para um teste confiável, o intervalo entre 0.7 e 0.9 para este indicador.
4. Resultados
O ENEM 2018 teve 5513662 inscritos confirmados, dos quais 1352566 (≈ 24.53%) não compareceram aos dois dias de prova. Nesse ano, percebeu-se que as 30 habilidades5 da Matriz de Referências do exame foram avaliadas em 1 ou 2 itens. Também neste ano, um item (item 28) foi anulado do exame por não ser inédito (Brasil, 2018a), dessa forma, excepcionalmente para 2018, a prova de Matemática do ENEM contou com 44 itens.
4.1 Análises dos itens da prova de Matemática do ENEM 2018
O processo de estimação dos parâmetros dos itens e dos respondentes foi realizado, mediante a aplicação do modelo logístico de 3 parâmetros da TRI, e a unidimensionalidade da prova foi verificada ( 𝜆 2 =1.14, 𝜆 =0.96, 𝑝 = .07). Quatro itens apresentaram problemas de ajuste ao modelo: item 16 ( χ 2 G=10, N = 68438 =29.54, p <.001), item 21 ( χ 2 G=10, N = 68438 =18.52, p=.03), item 38 ( χ 2 G=10, N = 68438 =23.68, p < .01) e item 45 ( χ 2 G=10, N = 68438 =22.45,p < .01). Estes itens foram excluídos, e o processo de estimação foi refeito, resultando em 40 itens (90.91%) bem ajustados.
A tabela 1 apresenta uma análise individual de cada um desses itens, destacando a posição que ele ocupa na prova, a habilidade (Hab) na qual ele se relaciona6, o percentual de acerto (%), os parâmetros de discriminação (a), dificuldade (b) e acerto ao acaso (c) e seus respectivos erros-padrão de estimação (ep), que representam as distâncias médias com que os valores observados se encontram da curva de regressão, e que podem ser um indicador da qualidade do ajuste e da precisão da estimação. Em suma, estão mais bem ajustados os itens que apresentam menores erros-padrão para as estimativas dos parâmetros dos itens.
Tabela 1 Análise individual de cada item da Prova de Matemática do ENEM/Brasil 2018
| Item | Hab | % | A | ep(a) | b | ep(b) | c | ep(c) |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 21.54 | 2.01 | 0.07 | 2.32 | 0.03 | 0.18 | < 0.01 |
| 2 | 18 | 24.26 | 0.87 | 0.08 | 3.50 | 0.05 | 0.19 | < 0.01 |
| 3 | 22 | 20.09 | 1.44 | 0.08 | 2.61 | 0.05 | 0.16 | < 0.01 |
| 4 | 26 | 16.59 | 2.26 | 0.06 | 2.93 | 0.06 | 0.16 | < 0.01 |
| 5 | 13 | 32.38 | 1.03 | 0.06 | 1.94 | 0.03 | 0.20 | 0.01 |
| 6 | 3 | 25.05 | 2.40 | 0.06 | 2.22 | 0.03 | 0.22 | < 0.01 |
| 7 | 20 | 25.31 | 3.68 | 0.09 | 1.19 | < 0.01 | 0.13 | < 0.01 |
| 8 | 16 | 25.12 | 2.60 | 0.09 | 1.82 | 0.02 | 0.20 | < 0.01 |
| 9 | 5 | 36.85 | 1.03 | 0.09 | 0.68 | 0.08 | 0.07 | 0.02 |
| 10 | 27 | 27.41 | 2.25 | 0.07 | 1.59 | 0.01 | 0.19 | < 0.01 |
| 11 | 10 | 33.23 | 3.10 | 0.07 | 0.97 | 0.01 | 0.17 | < 0.01 |
| 12 | 4 | 31.30 | 2.53 | 0.05 | 0.91 | 0.01 | 0.11 | < 0.01 |
| 13 | 19 | 28.26 | 2.04 | 0.08 | 1.84 | 0.02 | 0.21 | < 0.01 |
| 14 | 14 | 31.19 | 1.63 | 0.08 | 2.31 | 0.04 | 0.26 | < 0.01 |
| 15 | 29 | 37.66 | 0.21 | 0.01 | 2.85 | 0.08 | 0.13 | 0.02 |
| 16/1 | 23 | 30.46 | - | - | - | - | - | - |
| 17 | 20 | 18.77 | 3.06 | 0.08 | 2.64 | 0.03 | 0.18 | < 0.01 |
| 18 | 8 | 26.80 | 0.76 | 0.09 | 3.10 | 0.06 | 0.18 | 0.01 |
| 19 | 30 | 16.76 | 1.90 | 0.03 | 2.96 | 0.06 | 0.15 | < 0.01 |
| 20 | 7 | 23.64 | 2.29 | 0.06 | 1.42 | 0.01 | 0.13 | < 0.01 |
| 21/1 | 29 | 16.83 | - | - | - | - | - | - |
| 22 | 11 | 16.72 | 2.48 | 0.06 | 1.77 | 0.01 | 0.10 | < 0.01 |
| 23 | 5 | 20.61 | 1.89 | 0.05 | 2.66 | 0.05 | 0.18 | < 0.01 |
| 24 | 9 | 78.33 | 1.32 | 0.03 | -1.22 | 0.07 | 0.07 | 0.02 |
| 25 | 27 | 32.67 | 3.29 | 0.09 | 1.26 | 0.01 | 0.22 | < 0.01 |
| 26 | 22 | 10.95 | 2.69 | 0.02 | 2.96 | 0.06 | 0.18 | < 0.01 |
| 27 | 2 | 26.97 | 1.88 | 0.05 | 1.39 | 0.01 | 0.14 | < 0.01 |
| 28/2 | 4 | - | - | - | - | - | - | - |
| 29 | 3 | 34.60 | 1.32 | 0.04 | 1.14 | 0.02 | 0.14 | < 0.01 |
| 30 | 2 | 26.13 | 2.76 | 0.06 | 2.60 | 0.04 | 0.25 | < 0.01 |
| 31 | 28 | 22.01 | 3.20 | 0.08 | 1.75 | 0.01 | 0.17 | < 0.01 |
| 32 | 28 | 20.98 | 3.02 | 0.08 | 1.80 | 0.01 | 0.16 | < 0.01 |
| 33 | 24 | 38.23 | 2.02 | 0.05 | 0.96 | 0.01 | 0.19 | < 0.01 |
| 34 | 11 | 24.79 | 2.55 | 0.09 | 2.74 | 0.05 | 0.24 | < 0.01 |
| 35 | 19 | 20.30 | 2.61 | 0.09 | 1.93 | 0.01 | 0.16 | < 0.01 |
| 36 | 6 | 24.34 | 2.04 | 0.05 | 1.38 | 0.01 | 0.12 | < 0.01 |
| 37 | 25 | 48.17 | 0.73 | 0.01 | 0.15 | 0.04 | 0.11 | 0.01 |
| 38/1 | 15 | 20.21 | - | - | - | - | - | - |
| 39 | 17 | 29.58 | 1.56 | 0.09 | 3.26 | 0.05 | 0.28 | < 0.01 |
| 40 | 21 | 30.25 | 0.59 | 0.08 | 3.43 | 0.01 | 0.20 | 0.02 |
| 41 | 26 | 19.28 | 1.93 | 0.06 | 1.96 | 0.02 | 0.13 | < 0.01 |
| 42 | 25 | 32.23 | 2.52 | 0.06 | 1.22 | 0.01 | 0.20 | < 0.01 |
| 43 | 21 | 18.02 | 1.67 | 0.09 | 3.33 | 0.05 | 0.17 | < 0.01 |
| 44 | 8 | 21.36 | 2.02 | 0.07 | 1.85 | 0.01 | 0.15 | < 0.01 |
| 45/1 | 12 | 21.64 | - | - | - | - | - | - |
¹/ Itens excluídos por apresentarem problemas de ajuste ao modelo logístico de 3 parâmetros.
²/ A questão 28 foi anulada do exame por já ter aparecido em outro vestibular.
Fonte: Elaboração própria, a partir dos resultados das análises, 2020.
Observe que, numa análise global, a prova pode ser considerada como difícil. A grande maioria dos itens teve o parâmetro de dificuldade positivo (𝑏>0), o que indica que estão acima do ponto médio da escala de habilidades (𝜃=0). Observe, também, que 5 itens (2, 18, 39, 40 e 43) apresentaram valores para o parâmetro de dificuldade fora do intervalo aceitável, proposto por Alnabhan e Harwell (2001). Dentre os demais, os itens 24 e 26 se constituem como os itens de menor e maior índice de dificuldade, respectivamente, sob a ótica da TRI. Estes itens também foram os que obtiveram maior e menor percentual de acerto. Para fins de ilustração, eles estão representados pelas figuras 1 e 2.
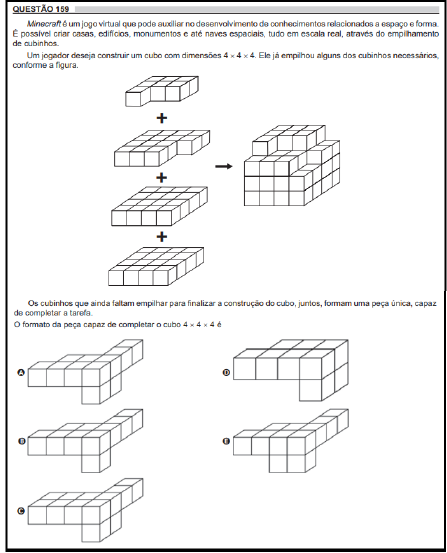
Fonte: INEP/MEC (Brasil, 2018b).
Figura 1 Item 24 (posição 159) da Prova de Matemática do ENEM/Brasil 2018

Fonte: INEP/MEC (Brasil, 2018b).
Figura 2 Item 26 (posição 161) da Prova de Matemática do ENEM/Brasil 2018
Em ambos, foram exigidos dos respondentes conhecimentos geométricos para a solução. Entretanto, as habilidades relacionadas a eles são distintas. O item 24 se refere a habilidade 9: “utilizar conhecimentos geométricos de espaço e forma na seleção de argumentos propostos como solução de problemas do cotidiano” (Brasil, 2009b, p. 6). Para respondê-lo corretamente o estudante precisava identificar que a peça representada na alternativa 𝐴 é a única que se encaixa no sólido obtido, formando um cubo 4×4×4.
O item 26 se refere a habilidade 22: “utilizar conhecimentos algébricos/geométricos como recurso para a construção de argumentação” (Brasil, 2009b, p. 6). Em termos práticos, o estudante poderia se apropriar do conceito de distância entres pontos, da geometria analítica, para conceber a relação entre as distâncias trazidas pelo enunciado do item. Assim, o estudante seria capaz de encontrar uma equação e, através de sua resolução, determinar a maior distância possível entre os bombeiros, cujo valor correto é o de 40 metros.
Quanto a discriminação dos itens, apenas 1 (item 15) apresentou parâmetro insatisfatório (𝑎<0.5). O item com maior índice de discriminação 𝑎=3.68 é o item 7, relacionado à habilidade 20: “interpretar gráfico cartesiano que represente relações entre grandezas” (Brasil, 2009b, p.6). Este item é representado pela figura 3.

Fonte: INEP/MEC (Brasil, 2018b).
Figura 3 Item 7 (posição 142) da Prova de Matemática do ENEM/Brasil 2018
Para respondê-lo corretamente, o estudante precisava, primeiramente, observar que para ter uma maior força gravitacional é preciso que se tenha a maior massa (menor raio), considerando um raio (massa) constante. Os satélites A e B possuem um mesmo raio, o que nos permite afirmar que 𝐹 𝐴 < 𝐹 𝐵 , visto que B possui uma massa superior à de A. Analogamente, 𝐹 𝐶 < 𝐹 𝐴 , visto que eles possuem a mesma massa e que o raio de A é menor do que o de C. Assim, por transitividade, conclui-se que 𝐹 𝐶 < 𝐹 𝐴 < 𝐹 𝐵 .
4.2 Análise global da prova de Matemática do ENEM 2018
Quanto a análise global da prova, concluiu-se, através do cálculo do coeficiente Alpha de Cronbach, pela aceitabilidade da confiabilidade dos seus resultados (𝛼=0.72). O escore (total de itens corretamente respondidos) médio obtido no teste foi de 11.88, com desvio-padrão 5.08. Já a proficiência dos respondentes, mensurada na Escala de Proficiências do ENEM, possui média 500.06 e desvio-padrão 100.31. As figuras 4 e 5 representam os gráficos de distribuição de frequências dessas variáveis.
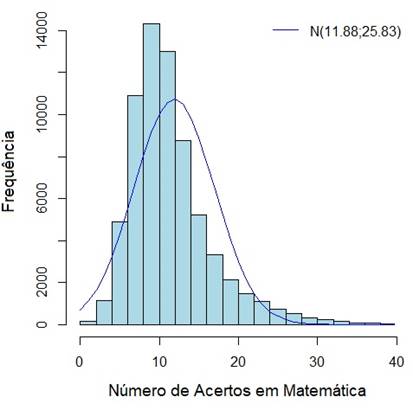
Fonte: Elaboração própria, a partir dos resultados das análises, 2020.
Figura 4 Frequência dos escores obtidos na prova de Matemática do ENEM/Brasil 2018
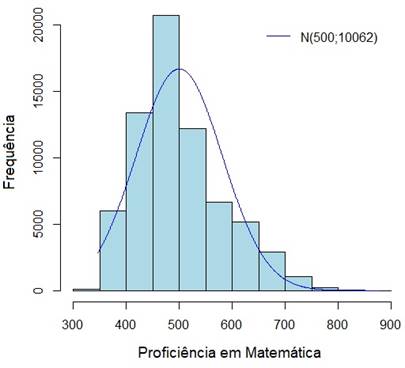
Fonte: Elaboração própria, a partir dos resultados das análises, 2020.
Figura 5 Frequência das proficiências obtidas em Matemática do ENEM/Brasil 2018
A aplicação do teste de Kolmogorov-Smirnov sobre os escores e sobre as proficiências obtidas na prova de Matemática do ENEM 2018 indicou a rejeição da hipótese de normalidade em ambos os conjuntos de dados (𝐷(68438) = 0.14,p <.001 e D(68438)=0.09,p <.001, respectivamente). A figura 6 expressa a relação entre essas variáveis, significativa pelo teste do coeficiente de correlação de postos de Spearman ( 𝑟 𝑆 (68438)=.84, 𝑝<.001).
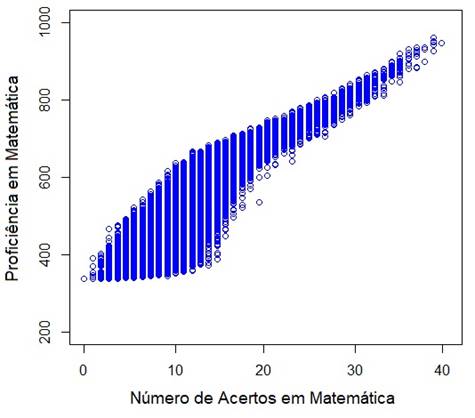
Fonte: Elaboração própria, a partir dos resultados das análises, 2020.
Figura 6 Relação entre o escore e a proficiência da Prova de Matemática do ENEM/Brasil 2018
É possível verificar também, por meio da figura 6, uma grande variabilidade de proficiências estimadas pela TRI, obtidas por estudantes com um mesmo número de acertos, especialmente para aqueles que obtiveram entre 12 e 17 acertos. A tabela 2 representa a variação obtida nas notas desses estudantes, ilustrando esta situação.
Tabela 2 Estatísticas descritivas obtidas para as proficiências de Matemática do ENEM 2018
| Número de Acertos | Nota Mínima | Nota Média | Nota Máxima | Amplitude | Coeficiente de Variação |
|---|---|---|---|---|---|
| 12 | 387 | 540.4 | 671.5 | 284.5 | 9.40% |
| 13 | 391.4 | 564.1 | 697.9 | 306.5 | 9.37% |
| 14 | 405.6 | 587.8 | 698.2 | 292.6 | 8.73% |
| 15 | 403.7 | 614.5 | 715.4 | 311.7 | 7.67% |
| 16 | 421 | 639.7 | 720.9 | 299.9 | 6.81% |
| 17 | 481.1 | 661.3 | 728.8 | 247.7 | 5.40% |
Fonte: Elaboração própria, a partir dos resultados das análises, 2020.
Como pode-se observar na tabela 2, considerando a amostra analisada, para estudantes com 13 e 15 acertos esta variação pode ultrapassar os 300 pontos na proficiência. A coerência das respostas é a principal responsável pela variação das notas de estudantes com o mesmo número de acertos na prova, se constituindo como um fator essencial para o êxito no ENEM, como já indicado por Maceno e Guimarães (2013), Nascimento, Souza e Oliveira (2020) e Pasquali (2018).
Para fins de ilustração, suponhamos que dois estudantes X e Y, com 15 acertos cada, tenham proficiências estimadas pela TRI iguais a 403.7 e 715.4, respectivamente. O que levou Y a ter uma nota tão superior à X está relacionado à coerência pedagógica das suas respostas. Enquanto o primeiro provavelmente tenha acertado apenas as questões mais difíceis da prova e errado as mais fáceis, o segundo obteve um comportamento contrário, como esperado pedagogicamente.
Por mais subjetivo que possa parecer esta análise, sob a ótica da TRI, caso um estudante acerte um item mais difícil e erre um mais fácil, este acerto pode ser considerado como casual pela TRI, fator controlado pelo parâmetro 𝑐 do modelo logístico de 3 parâmetros, adotado.
Em tempo, isto não significa que a nota de um respondente diminua ou que ele não pontue quando o sistema detecta acerto casual, apenas que o item corretamente respondido por ele, não possui tanto valor quanto possuiria se houvesse coerência pedagógica nas respostas do estudante. Em suma, espera-se que o estudante acerte aos itens que estão abaixo do seu nível de proficiência. Caso contrário, sua nota não tende a ser alta (Brasil, 2012).
Em contrapartida, uma análise descritiva da figura 11, também permite inferir que esta variabilidade é bem menor entre alunos com menos de 5 ou mais de 35 acertos na prova. Entretanto, o número de estudantes que se encaixam nesses intervalos é pequeno se comparado ao total de respondentes da prova.
5. Conclusões
A política de implantação da TRI nas avaliações em larga escala, no Brasil, teve início em 1995 com a aplicação da metodologia no Sistema de Avaliação da Educação Básica (SAEB). Entretanto, foi apenas em 2009 que ela se tornou alvo de discussões e debates em todos os cenários educacionais e na mídia, mediante sua adoção pelo ENEM, devido ao impacto direto do exame nas políticas de democratização do acesso ao Ensino Superior brasileiro.
A proposta, até então novidade, gerou muitas dúvidas quanto a sua operacionalização e quanto à confiabilidade de seus resultados. Ainda hoje ela é vista com certa desconfiança e entender o seu funcionamento é um desafio tanto para os estudantes, quanto para professores, gestores e pesquisadores educacionais, apontando para a necessidade de estudos direcionados a avaliar a estrutura do exame, como o aqui apresentado, desenvolvido com o objetivo de analisar a qualidade psicométrica da prova de Matemática da edição 2018 do ENEM/Brasil.
Os resultados deste estudo indicaram uma prova com confiabilidade satisfatória (𝛼=0.72) e composta por itens que, em sua maioria, se ajustam bem ao modelo logístico de 3 parâmetros da TRI, adotado pelo exame. Apenas os itens 16, 21, 38 e 45 apresentaram problemas quanto ao ajuste. O pressuposto da unidimensionalidade da TRI foi verificado por meio da análise paralela modificada, permitindo a estimação dos parâmetros dos itens e da proficiência dos respondentes.
Para fins de comparação, a meta-análise realizada por Travitzki (2017) sinalizou para a confiabilidade da prova de Matemática aplicada na edição de 2011 do exame (𝛼=0.84), ano em que todos os itens se ajustaram bem ao modelo utilizado. Em contrapartida, conforme análise também realizada pelo autor, a prova de Matemática de 2009 apresentou confiabilidade insuficiente 𝛼=0.59 , sendo que 11% dos itens que a compõem apresentaram problemas de ajuste. O pressuposto da unidimensionalidade da TRI foi atendido em ambas as edições. Na meta-análise realizada por Toffoli (2019), que considerou a prova de Matemática do ENEM 2015, análises estatísticas de confiabilidade e de qualidade de ajuste ao modelo não foram apresentadas. Ademais, a autora não indicou se o pressuposto da unidimensionalidade da prova foi atendido.
Quanto aos parâmetros psicométricos estimados, segundo os critérios definidos neste estudo, foram identificados 6 itens com problemas estruturais, sendo 1 referente ao coeficiente de discriminação (item 15) e 5 referentes ao coeficiente de dificuldade (itens 2, 18, 39, 40 e 43). Para esses últimos, ressalta-se que todos encontraram-se acima do limite estabelecido (𝑏>3.0), indicando que para respondê-los corretamente é necessário que o estudante possua um alto grau de conhecimento. Ressalta-se, também, conforme exposto na tabela 1, que 2 desses itens (40 e 43) se referem a uma mesma habilidade (habilidade 21): “resolver situação-problema cuja modelagem envolva conhecimentos algébricos” (Brasil, 2009b, p. 6).
Dessa forma, de acordo com as análises empreendidas, 22.7% dos 44 itens da prova de analisada apresentaram comportamento empírico fora dos padrões de qualidade considerados, porcentagem bem abaixo dos 49% encontrados por Travitzki (2017), para a prova de Matemática do ENEM 2009, e dos 57.8% encontrados por Toffoli (2019), para a prova de Matemática do ENEM 2015, porém acima dos 18% encontrados por Travitzki (2017), para a prova de Matemática do ENEM 2011.
Esses resultados nos levam a concluir que uma porcentagem considerável dos itens de Matemática do ENEM 2018 apresenta parâmetros psicométricos insatisfatórios e, tendo em vista que qualquer imprecisão sinalizada pode comprometer a validade dos seus resultados, sugere-se que os processos que envolvem a criação, revisão, testagem e calibração dos itens sejam aprimorados, de modo a garantir a isonomia do exame.
Ademais, mediante análise da intensidade da associação entre o total de itens respondidos corretamente (escore) e a proficiência dos estudantes, estimada pela TRI, foi possível verificar, empiricamente, a importância da coerência pedagógica para um bom desempenho no ENEM, o que parece-nos interessante abordar, mais detalhadamente, em estudos futuros.
Espera-se que esta pesquisa esclareça alguns conceitos da psicometria e atue como um instrumento de difusão de conhecimentos sobre a TRI, contribuindo para a alocação de discussões acerca desta teoria no ambiente escolar, em eventos científicos e em trabalhos de caráter acadêmico.