Revista de Biología Tropical
versão On-line ISSN 0034-7744versão impressa ISSN 0034-7744
Rev. biol. trop vol.47 no.3 San José Set. 1999
de Guerrero, México
Apolinar Santamaría1 Ernesto A. Chávez2 3
Recibido 24-VIII-1998. Corregido 22-I-1999. Aceptado 2-II-1999.
Abstract
Red snapper (Lutjanus peru) fishery was analyzed from landings and catch records. Stock age structure was reconstructed after the parameter values of the von Bertalanffy growth model, the length-weight relationship, ages and the natural mortality coefficient through each of nine years of catch records. The Fisat software package was applied to assess population parameters, whose estimates are, for the von Bertalanffy growth model, K = 0.1442 to 0.38; to = -0.2; L = 87 cm; W = 9.4 Kg , and the natural mortality coefficient (M) after several methods (0.14 to 0.38). Cohort size was assessed by the virtual population analysis (VPA), estimating population size in 5.2*106 fish with a biomass of 8 454 tonnes. Current fishing mortality F, ranges from 0.06 to 1.13, depending upon the chosen M value; according to this, when the M value used is low, the results suggest that the stock is underexploited, and vice versa. The yield per recruit model applied suggests improvements to the management strategy. The model indicates recruit overfishing because very small fish are the main target (tc < 1), nearly 50 % of fish caught are immature and under one year of age. Optimum yield levels correspond to first catch age of 2 to 3 years and a fishing mortality of F = 0.35, suggesting the need of limiting small fish catch of to a minimum of 2 year old specimens.
Key words
Lutjanus peru, Lutjanidae, population dynamics, stock assessment, west central Mexico.
Casi toda la costa occidental mexicana se caracteriza por ser de tipo rocoso, tiene una plataforma estrecha y constituye un hábitat relativamente homogéneo (Rodríguez-de la Cruz 1988). El área de estudio, como la mayor parte de las costas de México es de tipo tropical (con temperaturas que oscilan entre 24.1oC y 31.0oC), y se localiza entre las coordenadas siguientes: 99°08a 99°43 W y 17°20 a 17°32 N. Las pesquerías artesanales de esta parte del país son típicamente pluriespecíficas y con frecuencia aportan volúmenes de captura por especie relativamente bajos. Cruz-Romero et al. (1988, 1994) han descrito las características de esta pesquería para el Estado de Colima; en ella, la pesca se realiza principalmente mediante el uso de línea y anzuelo. Las operaciones de pesca son diurnas y los viajes de pesca duran varias horas durante la mañana. En las costas de Guerrero, México, se explotan a dos especies de pargo, el "huachinango" Lutjanus peru, y el "pargo flamenco" L. guttatus como objetivos principales; además se extraen otras especies cuyos volúmenes anuales con frecuencia superan las 400 toneladas. Los muestreos se realizaron muy cerca del puerto de Acapulco, en el Estado de Guerrero, donde se concentra el producto desembarcado. De acuerdo con los registros estadísticos de la Delegación Federal de Pesca en el Estado, las capturas de esta especie fluctúan entre 94.4 t en 1984, y 761.5 t en 1993 (Cuadro 1).
Evaluaciones de la tasa de crecimiento de esta especie han sido hechas previamente por Ruiz-Luna et al. (1985) para las costas de Michoacán. El rendimiento de un conjunto de pargos que incluye al huachinango, ha sido evaluado para la costa de Colima, México inicialmente con modelos de producción excedente (Cruz-Romero et al. 1988) y mas recientemente mediante un análisis de simulación basado en la estructura por edades de sus poblaciones (Cruz-Romero et al. 1996); como resultado de esos estudios, el nivel de rendimiento máximo sostenible de L. peru fue estimado en 400 tons. Gutiérrez (1990) por su parte, analiza la población en Costa Rica, encontrando que en 1985 se encontraba considerablemente sobreexplotada. Rocha-Olivares y Gómez-Muñoz (1993), analizan las marcas de crecimiento en los otolitos y demuestran su validez para evaluar la tasa de crecimiento.
Materiales y Métodos
Se hicieron muestreos mensuales de la frecuencia de longitudes utilizando las descargas comerciales durante 11 meses entre octubre de 1992 y diciembre de 1993, y un muestreo adicional en enero de 1995. Para la identificación de los grupos de edad se aplicaron los métodos de Hasselblad (1966) y de Bhattacharya (1967), ambos contenidos en el paquete de programas Fisat, y que tienen la función de identificar los componentes normales en las distribuciones de frecuencias de longitud.
También se registraron datos de peso-longitud, con los que se estableció la correspondencia entre estas dos variables mediante una regresión logarítmica de la forma P=aLb, donde P es el peso en Kg y L la longitud total en cm de los peces; después de hacer el análisis de los datos de la frecuencia de longitudes, se procedió a transformar las longitudes medias de cada edad a sus pesos correspondientes. Para analizar la tasa de crecimiento según el modelo de von Bertalanffy, cuya fórmula es l= [L-eb-K(t-to)] , se utilizó el paquete de programas Fisat (Gayanilo et al. 1996), donde, l = longitud (cm) a la edad t; L
= Longitud asintótica; K= Coeficiente proporcional a la tasa de catabolismo; to= Parámetro de ajuste, equivalente a la edad teórica, correspondiente a una longitud igual a 0. Al conocerse la tasa de crecimiento se determinó la estructura por edades. Para estimar las variancias de los parámetros de la tasa de crecimiento, el análisis de los datos se hizo a base de muestreo con reemplazamiento sucesivo de las muestras; en cada caso se eligió el valor mas alto del índice de bondad del ajuste (Rn), que de acuerdo con Gayanilo et al. (1996), se define como Rn = 10 ESP/ASP/10 donde, ASP es la Suma de Picos Disponible y ESP es la Suma de Picos Explicada; la primera se estima como la suma de los "mejores" valores de los picos "disponibles", y la segunda se determina sumando todos los picos y cruzamientos con una curva de crecimiento. Con el paquete Fisat también se hizo la estimación de las mortalidades natural (M) y por pesca (F), la evaluación del recurso y una parte del diagnóstico de la pesquería. Para estimar el coeficiente M, también se aplicaron los métodos de análisis de Rikhter y Efanov (1976) modificado (el coeficiente Tm50 del modelo, o sea, la edad en que madura el 50 % de la población, fue substituído por el que describe la mitad de la longevidad máxima, equivalente al 99 % de la longitud asintótica, o sea, tT= 4.6/K, pues se encontró que en su versión original subestima la mortalidad en poblaciones longevas y estima un valor de M= 0 cuando la longevidad es de 47.5 años), de Hoenig (1983), Alagaraja (1984), descritos por Sparre y Venema, (1992); así como el de Pauly (1980a), el de Djabali et al. (1993), ambos con una temperatura de 28.5oC y el propuesto por Chávez (1995).
Después que los parámetros del modelo de crecimiento de von Bertalanffy (L, K, to), así como el de M fueron evaluados, y con los datos de las estadísticas de la captura comercial del período de 1983 a 1991 (Fig. 1a, Cuadro 1), se procedió a analizar la población: el tamaño de cada cohorte fue determinado con el método de análisis de la población virtual (VPA), y se hizo una estimación del tamaño absoluto de cada grupo de edad (Pt), así como en sus biomasas (wt).
Como herramienta para el diagnóstico de la pesquería, se aplicó el modelo de Beverton y Holt (1957) que permitió evaluar el rendimiento por recluta y cuya función es Y/R= FtrtT Nt Wt dt; en esta ecuación, Y= Rendimiento; R= Reclutas; r= Edad de reclutamiento; T= Edad máxima; F= Mortalidad por pesca; Nt= Número de individuos a la edad t; Wt= peso de los individuos a la edad t y dt= Diferencial del tiempo. Para el período que abarcan los registros de las descargas comerciales, se estimaron los valores de la mortalidad por pesca (F) y mediante un proceso iterativo se estableció su correspondencia con el valor de la captura. El número de clases de edad fue definido mediante una estimación de la longevidad (tT = 3/K), derivada de la ecuación de von Bertalanffy, al considerar que por lo menos el 95% de la población tiene la probabilidad de alcanzar la longitud asintótica (Pauly 1980b, Chávez 1995).
Resultados
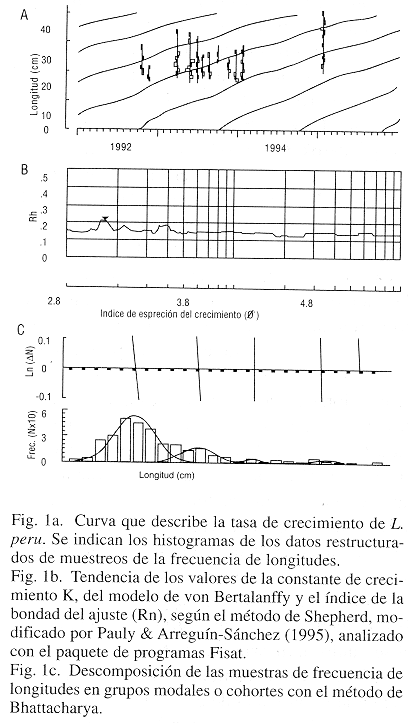
Edad y crecimiento: De los parámetros estimados de la ecuación de von Bertalanffy, cuyo ajuste a los datos se describe en la Fig. 1a, los valores promedios, utilizados para evaluar la población son los siguientes: L = 80.85 cm; K= 0.1442; to=-0.23; C= 0.6769 wp= 0.4 y Rn= 0.2462. El error estándar de los dos primeros es 2 y 0.0216 respectivamente. El análisis de regresión permitió la transformación de las longitudes medias de cada edad a sus pesos correspondientes; los valores de los parámetros son a= 0.0000545 y b= 2.727 (Cuadro 2). El primero corresponde al factor de condición y el segundo es la constante de proporcionalidad entre el peso y la longitud; con esta relación se determinó el peso asintótico, cuyo valor es W
= 8.6824 Kg. Para la estimación del parámetro K también se utilizó el método de barrido de valores de Shepherd, modificado por Pauly y Arreguín-Sánchez (1995, Fig 1b), contenido en el programa Elefan. Además de los métodos antes citados, se aplicaron los de Bhattacharya y de Hasselblad para la separación de grupos de edad, como grupos normales en el total muestral de la serie de datos de longitud; en el primer caso (Fig. 1c), se identificaron cinco grupos de edad y en el segundo se discriminó un total de diez (Fig. 2a), el cual se considera mas lógico al tomar en cuenta la longevidad de esta especie, así como las longitudes que alcanzan los animales. La longevidad estimada, a nivel del 95 %, resultó ser de tT = 21años.
Captura de L. peru registrada para cada región del Estado de Guerrero, México durante el período 1984-1993, Kg.
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
Los promedios* corresponden al periodo 1985-1993. Los registros proceden de las estadísticas de la Delegación Federal de Pesca en el Estado de Guerrero. Las dos últimas columnas indican los valores estimados de la Biomasa de la población, B (t) y de la mortalidad por pesca, F.
Valores de los parámetros de la población de L. peru estimados por varios métodos.
| |
| | | |
| | |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| |
| | | | | | |
| | | | | | | | |
| | | | | | | | |
L = Longitud asintótica (cm), W= Peso asintótico (Kg), K= Constante de crecimiento, to= Parámetro de ajuste
de la curva de crecimiento en el origen; a= Coeficiente de proporcionalidad de la relación peso-longitud; b=
Exponente de L en la relación peso-longitud; C= Coeficiente relacionado con la estacionalidad de la tasa de
crecimiento; wp= Punto de invierno, que se refiere a la estacionalidad del proceso reproductivo; Rn= Indice de
bondad del ajuste (Gayanilo et al. 1996).
Patrón estacional de reclutamiento: La dispersión de los datos y su ajuste a la tasa de crecimiento permiten establecer la temportalidad del proceso reproductivo. La distribución de frecuencias de los tamaños registrados en las muestras hace posible reconstruir la historia reproductiva de la población en el transcurso del ciclo anual, lo que se pone en evidencia en la Fig. 2b, según la cual se identifican dos períodos de reclutamiento a la pesquería, el primero de ellos mas intenso y con mayor variancia, tiene su valor máximo en febrero, durante el cual se incorpora mas del 75% de los reclutas; el segundo ocurre entre agosto y septiembre y a esta porción corresponde solo una fracción aproximada al 20% del reclutamiento anual.
Mortalidad: La mortalidad natural determinada mediante los métodos antes señalados, indica que los valores obtenidos (Cuadro 3), fluctúanentre 0.1427 y 0.3839 (no se tomaron en cuenta las estimaciones hechas con los métodos de Djabali et al., por que se considera que subestiman demasiado el valor del parámetro, ni el de Pauly que utiliza valores de crecimiento en peso, por que lo sobreestima). El valor adoptado en otras etapas del análisis es el del método propuesto por Pauly que utiliza los parámetros de crecimiento longitudinal, con M= 0.3839. Con este valor, la razón M/K, parámetro útil para fines comparativos (Beverton y Holt 1957) es de M/K= 2.66, con una relación de las longitudes de selección de Lc/L = 0.15.
Valores del coeficiente de mortalidad natural de L. peru estimados con métodos propuestos por varios autores.
| M | Observaciones (Remarks) | Modelo utilizado (Source) |
| 0.1979 | Con Tm50=tT/2 | Rikhter & Efanov, 1976 |
| 0.3639 | Con parámetros de crecimiento de longitud* | Pauly, 1980a |
| 0.8884 | Con parámetros de crecimiento de peso* | Pauly, 1980a |
| 0.1427 | Regresión de Z y longevidad | Hoenig (1983) |
| 0.1442 | Se asignó valor a la longevidad | Alagaraja, 1984 |
| 0.02376 | Con parámetros de crecimiento en longitud* | Djabali et al. 1993 |
| 0.04169 | Con parámetros de crecimiento en peso* | Djabali et al. 1993 |
| 0.1442 | Con el criterio de M=K | Chávez, 1995 |
Las ecuaciones utilizadas fueron tomadas de Sparre & Venema (1992), Djabali et al. (1993) y de Chávez (1995). El coeficiente Tm50 del modelo de Rikhter y Efanov o sea, la edad en que madura el 50 % de la población, fue substituÌdo por el que describe la mitad de la longevidad máxima (la equivalente al 99 % de la longitud asintótica, o sea, tT= 4.6/K).
Estructura de la población e intensidad de pesca: El promedio anual de la captura registrada para el Estado de Guerrero durante el período 1985-1993 es de 480 toneladas (Cuadro 1); en el último año analizado de la serie de datos (1991), el rendimiento fue de 762 toneladas. Los tamaños de cada cohorte en la población fueron determinados mediante el análisis de la población virtual basada en las longitudes (Fig. 2c); además de la estructura por edades que los datos de muestreo permiten reconstruir, se encontró que el valor encontrado de F= 0.10, puede considerarse bajo, dado que se encuentra a la tercera parte del valor requerido para alcanzar el rendimiento máximo de 1,130 t, que sería de F= 0.35. Las condiciones actuales de la pesquería establecen que las tasas de explotación (E= F/Z) que producen el rendimiento máximo es de Emax= 0.48, el rendimiento marginal E0.1= 0.047 y el rendimiento a 50 % de la población virgen, E0.5= 0.238.
Discusión
Reclutamiento: Como comúnmente ocurre con las especies de ambientes tropicales, la relativamente reducida variabilidad estacional determina la posibilidad de encontrar individuos en reproducción en cualquier época del año, como una respuesta directa inducida por la temperatura sobre la tasa metabólica, aunque otros factores, además de la temperatura, como el fotoperiodo, contribuyen a definir la amplitud de la temporada reproductiva, que con frecuencia se expresa como dos picos de mayor intensidad dentro de un proceso reproductivo casi permanente (Gunter 1957). Este proceso se complica con la influencia de la estacionalidad del área, el tamaño, la edad y diferencias entre las poblaciones de distintas localidades (Brett 1970) y lo que pudiera considerarse como una regla, cuenta con gran número de excepciones. El período del año mas favorable permite que una fracción mayoritaria de la población desove en ese lapso; sin embargo, en un ambiente poco variable (la temperatura, la salinidad y la concentración de oxígeno por ejemplo, no son limitantes), las presiones adaptativas inducidas por factores son menos severas que en ambientes menos estables (Margalef 1974) y esto permite que en el área de estudio al menos una parte de la población de L. peru se reproduzca a lo largo del año.
Edad y crecimiento: Los grupos de edad presentes en las capturas comerciales incluyen peces a partir de su primer año de vida; como ya se mencionó, la longevidad estimada (tT) es de 21 años y se considera que los peces maduran a la edad de 3. Los patrones de madurez y selectividad indican que cerca del 35 % de los animales mas chicos capturados (tc= 3) son inmaduros. La longitud total m·xima registrada (según Fischer et al. 1995), es de 95 cm; en cambio, a pesar de que la demanda orienta la pesquería y está dirigida a la captura de ejemplares chicos, eventualmente se capturan animales de 110 cm. Por otra parte, al examinar las estimaciones de la tasa de crecimiento hechas por Gutiérrez (1990), se observa que el valor de K que él encontró es excesivamente alto con respecto a su longitud asintótica y corresponde a situaciones que con muy poca frecuencia se dan en la naturaleza. En contraste, los valores de K encontrados por Cruz-Romero et al. (1996) para esta misma especie y para otras dos del mismo género oscilan entre 0.155 y 0.192, que son mas parecidos a los estimados en este trabajo; en los casos antes citados, corresponden a longevidades (definidas como 3/K) que fluctúan entre 15 y 19 años, en cambio, el valor estimado para el huachinango de Acapulco corresponde a una longevidad de 21 años. La estimación de K hecha por Gutiérrez (1990) en Costa Rica conduce a interpretar que la longevidad de esta especie es de solo 2 años, lo cual resulta poco lógico. Un sesgo en la estimación de la constante de crecimiento K afecta otros resultados en los que este valor es utilizado, como es el caso del valor de la mortalidad natural M y el de rendimiento relativo por recluta, según el modelo de Beverton y Holt (1957). Para verificar estas estimaciones, los datos del Cuadro 1 del trabajo de Gutiérrez (1990) fueron analizados mediante los métodos de Elefan y NSLCA (dentro de las opciones del paquete Fisat), encontrando valores de K que oscilan entre 0.3 y 0.56 y de L8 entre 84 y 103 cm (el mejor ajuste, de Rn= 0.228, corresponde al segundo valor). Una reflexión derivada de los resultados obtenidos con esos datos se refiere a que algunos de los muestreos que sirvieron de base para ese análisis, están sesgados hacia las tallas pequeñas, al igual que las analizadas en este trabajo. Los sesgos muestrales pueden pasar desapercibidos si no se tiene suficiente familiaridad con las tallas de los animales en la población que se esté analizando.
El desarrollo de FishBase (Froese y Pauly 1996, 1997) ha permitido la síntesis de un gran volumen de datos que permiten comparar los parámetros de las poblaciones de peces y aún predecir los valores aproximados de esos parámetros en especies poco conocidas. En estas condiciones, Pauly y Binohlan (1996), señalan que el patrón de crecimiento (= log10 K + 2log10L
) evaluado para las 12 especies de pargo mejor documentadas en FishBase (de un total de 43 lutjánidos, 27 de ellos del género Lutjanus), enfatiza la estrecha relación entre los parámetros K y L
para los peces en general y para los pargos en particular, con un valor que para esta Familia de peces oscila entre 2.53 y 3.273. La expresión del crecimiento expresada por el valor de
encontrado para L. peru con los valores de K y de L8 evaluados en este trabajo, es de
= 2.9759; este se encuentra muy cerca del punto medio del intervalo de valores encontrados por Pauly y Binohlan (1996, Cuadro 3) para los lutjánidos.
Mortalidad y tasa de explotación: La curva de supervivencia de la mayor parte de los animales acuáticos se caracteriza por una mortalidad absoluta muy alta durante los primeros meses de su ciclo de vida. Para la estimación de M, Pauly y Binohlan (1996) encontraron que para el grupo de los pargos (Lutjanidae) y meros (Serranidae), el parámetro K de la ecuación de von Bertalanffy es un buen predictor de M, confirmando las ideas de Ralston (1987) en el mismo sentido. En estas condiciones, la correspondencia entre la mortalidad y la longevidad es muy estrecha y tiene correlación inversa.
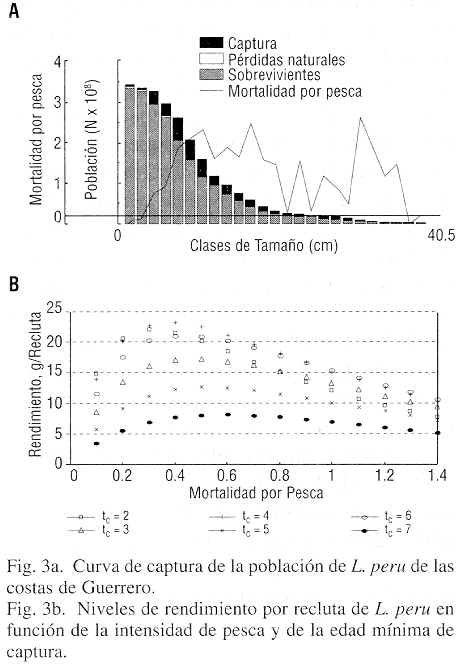
Poblaciones con longevidad larga como en L. peru se caracterizan por que su tamaño está limitado por la densidad y por lo mismo su tasa intrínseca de crecimiento es baja, lo que las hace muy vulnerables a la explotación; esta característica de su estrategia adaptativa impone la necesidad de aplicar un tipo de manejo tal que asegure la conservación de la pesquería ante la presión de pesca. Esto implica la necesidad de vigilar cuidadosamente la intensidad de la explotación, y también de evitar la captura de animales tan jóvenes como lo indican las muestras, ya que la sobreexplotación de juveniles debe ser evitada, pues acelera el agotamiento de la población. Cuando un recurso está sometido a una presión de pesca creciente, el número de grupos de edad tiende a reducirse desapareciendo primero los peces con mayor edad, los que en el caso de estudio, están pobremente representados (Fig. 2c). Al analizar la composición por edades a la curva de captura con los datos muestrales agrupados (Fig. 3a), la tendencia de los datos indica una correlación alta con una mortalidad total (Z) de 1.68, valor que al sustraerle el de M= 0.38 indica una mortalidad por pesca muy alta, de F= 1.3, que evidentemente indica una condición de sobrepesca muy severa.
Evaluación del recurso y estrategia de explotación: Al utilizar una apropiada representación de las tasas de cambio en los números de individuos en la población debidas a la pesca, es factible detectar estos cambios y estimar una combinación de valores tal que se pueda determinar el nivel de pesca que produzca un rendimiento máximo a largo plazo. A su vez, esto sirve de base para proponer estrategias de administración de la pesquería y evaluar los cambios mas probables en la población y en los factores económicos y sociales subyacentes.
Un objetivo común en el manejo de las pesquerías es la que persigue como meta el rendimiento máximo sostenible (RMS), que no significa otra cosa que la aplicación de los valores de la mortalidad por pesca tales que se traduzcan en los rendimientos máximos posibles a largo plazo. Al inducir diferentes presiones sobre la población explotada, es factible determinar el valor de F que produzca el rendimiento o captura máximos. En un modelo de simulación aplicado a la pesquería de tres especies de Lutjanus que incluyen a L. peru en la costa de Colima (Cruz-Romero et al. 1996), se probó un gran número de valores de F, entre 0.1 y 1.3, con un modelo basado en la estructura por edades y en todos los casos el valor mas alto de la captura se encontró con el valor de F= 0.7. En el caso de L. peru de las costas de Guerrero, se aplicó el modelo de Beverton y Holt (1957) con propósitos de diagnóstico, según se muestra en la Fig. 3b; de su examen se percibe que los valores mas altos del rendimiento por recluta corresponden a intensidades de pesca de F= 0.35 a 0.4 y a edades mínimas de captura de 2 y 3 años.
Un análisis del potencial productivo de la población a base de simulación (no incluído en este trabajo) indica, en contraste con los resultados del modelo de Beverton y Holt, que bajo las condiciones actuales de selectividad, el nivel de F= 0.35 produce el rendimiento máximo de 1130 t y que valores de F mas altos provocan una condición de sobrepesca que paulatinamente agota el recurso. Aunque los datos sugieren que el recurso aún está subexplotado; sin embargo, la sobrepesca de reclutas es evidente y se considera que esto es una distorsión en el modo de explotación que está fuertemente inducida por la demanda impuesta por un centro turístico de la magnitud de Acapulco, en donde los animales con "tamaño de plato" son objeto de una explotación mas intensa que los adultos, por que su valor relativo en el mercado es mayor que el de los animales grandes.
Criterios para regular la explotación: La tendencia de los valores de la mortalidad por pesca mostrada por los resultados hace aconsejable vigilar el nivel de esfuerzo que gravita sobre este recurso, para evitar el riesgo de sobreexplotar la pesquería al extremo de provocar una crisis social. Esta circunstancia señala la necesidad de que la pesquería sea evaluada y administrada de manera constante. La aplicación de varios métodos de evaluación conduce a conclusiones que pueden llevar a puntos opuestos, pues por una parte la diversidad de valores de la mortalidad natural oscila dentro de un intervalo indeseablemente amplio de valores y la adopción de alguno de ellos influye decisivamente en la evaluación y en el diagnóstico que se haga del estado de la explotación del recurso. Por ejemplo, al adoptar un valor bajo de M (0.1442), o en uno a base de simulación con M= 0.38, se concluye que el recurso se encuentra subexplotado, a la tercera parte del valor máximo que puede soportar de F; en cambio, la aplicación de otros procedimientos como el de la curva de captura o la elección de un valor de M mas alto en el modelo de rendimiento por recluta, hacen concluir que la población de huachinango del área de estudio está sobreexplotada. Independientemente de los resultados dados por cada método que se aplique, el valor de M que se elija es determinante del diagnóstico que se derive y por lo mismo la incertidumbre respecto al valor elegido dentro del intervalo de valores encontrados, es una clara limitante de los alcances de las conclusiones que se deriven de este trabajo. Por lo que se refiere a la talla mínima de captura, es indudable que se deben incrementar de manera inmediata las tallas mínimas legalmente aceptables, para reducir la sobreexplotación de reclutas, pues de no hacerlo, se corre el riesgo de limitar el potencial reproductivo del recurso.
Agradecimientos
Se agradecen las atinadas observaciones de un revisor anónimo. Belinda Valentín participó en el análisis de los datos a base de muestreo con reemplazamiento para estimar las variancias de los parámetros de crecimiento y en la depuración de las gráficas. Francisco Arreguín-Sánchez amablemente proporcionó los resultados verificados de los datos de Gutiérrez (1990). El co-autor es becario de la COFAA-IPN.
Resumen
La pesquería del huachinango Lutjanus peru, que se explota cerca de Acapulco, México, fue evaluada a través de muestreos de los desembarcos y de datos de captura. Se aplicó el paquete de programas Fisat para evaluar los parámetros de crecimiento del modelo de von Bertalanffy (K= 0.1442; to= -0.23; L = 80.8 cm; W = 6.824 Kg) y reconstruir la estructura por edades en la población en nueve años de datos de captura. El coeficiente de mortalidad natural M según varios métodos, oscila entre 0.14 y 0.38. El tamaño de cada cohorte a través del tiempo, evaluado con el método de análisis de la población virtual (VPA), estima una población de 5.2*106 peces explotados con una biomasa media de 8,454 t. La intensidad de explotación F, oscila entre 0.06 y 1.13 y depende del valor de M que se elija; según esto, se puede concluir que el recurso se encuentra subexplotado si el valor de M es bajo, o bien que se encuentra sobreexplotado si el valor elegido de M es alto. El modelo de rendimiento por recluta señala que hay sobrepesca de reclutas por que gravita sobre animales muy chicos (tc < 1), además, que los niveles óptimos corresponden a una edad mínima de captura de 2 a 3 años, y a una mortalidad por pesca de F= 0.35, lo cual sugiere la necesidad de limitar la captura de peces chicos imponiendo una talla mínima equivalente a la de 2 años de edad por lo menos, ya que cerca del 50% de los peces capturados tienen edades menores de un año y son inmaduros.
Referencias
Alagaraja, K. 1984. Simple methods for the estimation of parameters of assessing exploited fish stocks. Indian J. Fish. 31: 177-208. [ Links ]
Bhattacharya, C. G. 1967. A simple method of resolution of a distribution into Gaussian components. Biometrics 23: 115-135. [ Links ]
Beverton, R. J. H. & S. J. Holt. 1957. On the dynamics of exploited fish populations. Fish. Invest. Ser. II, 19, 533 p. [ Links ]
Brett, J. R. 1970. Temperature. p: 515-560. In Kinne, O. (ed.). Marine Ecology. Vol. I, Pt. I. Wiley-Interscience. 681 p. [ Links ]
Chávez, E. A. 1995. La mortalidad natural y su relación con la longevidad y la tasa de crecimiento. Jaina 6: 12. [ Links ]
Cruz-Romero, M., E. Espino & A. García. 1988. Estimación preliminar del índice de rendimiento máximo sostenible para la captura de escama ribereña. Universidad Autónoma de San Luis Potosí 10: 109-123. [ Links ]
Cruz-Romero, M., E. Espino & A. García. 1994. Pesquerías ribereñas del Pacífico mexicano. Atlas Pesquero y Pesquerías Relevantes de México. Secretaría de Pesca, Instituto Nacional de la Pesca. México, D. F. (CD-Rom). [ Links ]
Cruz-Romero, M., E. A. Chávez, E. Espino & A. García. 1996. Stock assessment of a snapper complex (Lutjanus spp.) of the eastern tropical Pacific. In Biology, fisheries and culture of tropical groupers and snappers. ICLARM Conf. Proc. No. 48: 330-336. [ Links ]
Djabali, F., A. Mehalilia, M. Koudil & B. Brahmi. 1993. Empirical equations for the estimation of natural mortality in Mediterranean teleosts. Naga ICLARM 16: 35-37. [ Links ]
Fischer, W., F. Krupp, W. Sneider, C. Sommer, K. E. Carpenter & V. H. Niem. 1995. Guía FAO para la identificación de especies para los fines de la pesca. Pacífico centro-oriental. Vertebrados. 3: 1201-1813. [ Links ]
Froese, R. & D. Pauly (eds.). 1996. FishBase96. Concepts, design and data sources. International Center for Living Aquatic Resources Management, Manila. [ Links ]
Froese, R. & D. Pauly, 1997. FishBase 97: a biological database on fish. International Center for Living Aquatic Resources Management. Manila (CD.ROM). [ Links ]
Gayanilo, F., P. Sparre & D. Pauly. 1996. The FAO-ICLARM Stock Assessment Tools (Fisat) [ Links ]
Users Guide. FAO Computerized Information Series. Fisheries, FAO, Roma. [ Links ]
Gunter, G. G. 1957. Temperature. In Hedgpeth, J. W. (ed.). Marine Ecology. Treatise on Marine Ecology and Paleoecology. Geol. Soc. America, Mem. 67, 1: 159-184. [ Links ]
Gutiérrez, R. 1990. Tasas de crecimiento, mortalidad, reclutamiento, rendimiento y biomasa relativos por recluta de Lutjanus peru (Perciformes: Lutjanidae) en el Pacífico noroeste de Costa Rica. Rev. Biol. Trop. 38: 441-447. [ Links ]
Hasselblad, V. 1966. Estimation of parameters for a mixture of normal distributions. Technometrics 8: 431-444. [ Links ]
Hoenig, J. M. 1983. Empirical use of longevity data to estimate mortality rates. Fish. Bull. NOAA/NMFS 81: 898-903. [ Links ]
Margalef, R. 1974. Ecología. Omega, Barcelona. 951 p. [ Links ]
Pauly, D. 1980a. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. Cons. CIEM 39: 175-192. [ Links ]
Pauly, D. 1980b. A selection of simple methods for the assessment of tropical fish stocks. FAO Fisheries Circular No. 729. FAO, Roma. 54 p. [ Links ]
Pauly, D. & F. Arreguín-Sánchez. 1995. Improving Shepherds length composition analysis for growth parameter estimations. Naga ICLARM 18: 31-33. [ Links ]
Pauly, D. & C. Binohlan. 1996. FishBase and AUXIM as tools for comparing life-history patterns, growth and Natural mortality of fish: Applications to snappers and groupers, p. 218-243. In Arreguín-Sánchez, J. L. Munro, M. Balgos & D. Pauly (eds.). Biology, fisheries and culture of tropical groupers and snappers. ICLARM Conf. Proc. 48, 449 p. [ Links ]
Ralston, S. 1987. Mortality rates of snappers and groupers, p. 375-404. In J. J. Polovina & S. Ralston (eds.) Tropical snappers and groupers: biology and fisheries management. Ocean Resour. Mar. Policy Ser. Westview Press. Boulder, Colorado. [ Links ]
Rikhter, V. A. & V. N. Efanov. 1976. On one of the approaches to estimation of natural mortality of fish populations. ICNAF Res. Doc., 76/VI/8: 12 p. [ Links ]
Rocha-Olivares, A. & V. Gómez-Muñoz. 1993. Validación del uso de otolitos para determinar la edad del huachinango del Pacífico Lutjanus peru (Perciformes Lutjanidae), en la bahía de la Paz y aguas adyacentes, B. C. S., México. Ciencias Marinas 19: 321-331. [ Links ]
Rodríguez-de la Cruz, M. C. 1988. Los recursos pesqueros de México y sus pesquerías. Secretaría de pesca, México, D. F. 237 p. [ Links ]
Ruiz-Luna, A., E. Girón, J. Madrid & A. González. 1985. Determinación de edad, crecimiento y algunas constantes biológicas del huachinango del Pacífico Lutjanus peru (Nichols y Murphy, 1922). Mem. VIII Congreso Nacional de Zoología. Saltillo, México, p: 188-201. [ Links ]
Sparre, P. & S. Venema. 1992. Introduction to tropical fish stock assessment. Part I, Manual. FAO Fisheries Technical Paper No. 306/1. [ Links ]
1 Centro Interdisciplinario de Ciencias Marinas, Instituto Politécnico Nacional (CICIMAR, IPN), Playa El Conchalito s/n, a. p. 592 La Paz, B. C. S., México 23070 Fax: +52.122 25322.
Correo electrónico: 1 asantama@vmredipn.ipn.mx; 2 echavez@vmredipn.ipn.mx
3 A quien debe dirigirse la correspondencia.











 uBio
uBio