Introducción
La importancia de la enseñanza y del aprendizaje de la matemática en la educación formal está fuera de discusión en la mayoría de los países. La matemática es una disciplina con presencia en múltiples actividades humanas, con aportes directos para explicar gran cantidad de fenómenos (Martínez-Padrón, 2005), por lo cual, se constituye en un pilar fundamental del sistema educativo (Van Vaerenbergh, 2019), lo que explicaría porqué es, probablemente, la única disciplina presente en todos los sistemas educativos y en sus diferentes niveles (Rico, 1998; Martínez-Padrón, 2005).
No obstante, también se ha señalado que una parte del estudiantado considera la matemática como una disciplina poco práctica, difícil, aburrida y abstracta (Gil, Guerrero y Blanco, 2006; Meza y Azofeifa, 2011), y, a veces, es valorada como la más impopular de las disciplinas (Martínez-Padrón, 2005, Romero, 2011). A lo anterior, se debe agregar la evidencia de que el aprendizaje de la matemática le “resulta arduo” al estudiantado (Van Vaerenbergh, 2019).
Aunado al problema de la baja aceptación social de la matemática por parte de numerosos grupos del estudiantado, prevalece el problema del rendimiento académico en la disciplina. Un indicador de la persistencia de esto puede encontrarse en los resultados de la prueba PISA 2015: el estudiantado obtiene peores resultados en matemática que en ciencias o en capacidad lectora. En el caso costarricense, las evaluaciones de PISA en las que se ha participado revelan que las diferencias entre hombres y mujeres en matemática han aumentado en contra de las mujeres (Programa Estado de la Educación, 2021).
Los resultados obtenidos en la enseñanza de la matemática en la educación media costarricense no son satisfactorios. Como indicador, se han utilizado los resultados de los exámenes de diagnóstico aplicados en las universidades estatales a estudiantes de nuevo ingreso (Ruiz, 2013). En el “Examen de diagnóstico en Matemática (DIMA)” de la Universidad de Costa Rica, los resultados para el periodo 2006-2010 muestran que más del 60% de estudiantes que aplican esa prueba obtuvo notas inferiores a 50 (en escala de 0 a 100) (Ministerio de Educación Pública, 2012). Los resultados en esa misma prueba en el año 2019 son peores, dado que solo el 6% de los estudiantes aprobó la prueba (Semanario Universidad, 2019).
La búsqueda de soluciones a los problemas de rendimiento académico en matemática ha llevado al desarrollo de numerosas investigaciones con predominio en lo cognitivo en un primer momento, más con la paulatina incorporación del componente afectivo desde hace algunas décadas (Gómez-Chacón, 2010; Pérez-Tyteca, 2012; Grootenboer y Marshman, 2015), porque “la gran cantidad de fracasos en el aprendizaje de las matemáticas pueden ser explicados por la aparición de actitudes negativas ocasionadas por factores personales y ambientales” (Gómez-Chacón, 2002). Así, cada vez más estudios reconocen la importancia de las emociones en los procesos educativos (Van Vaerenbergh, 2019), y, en el caso particular de la matemática, se ha tomado conciencia de que su enseñanza y aprendizaje responde a principios cognitivos, pedagógicos y didácticos, pero también a las actitudes de docentes y estudiantes (Sánchez, Segovia y Miñán, 2011), así como a la experiencia de ansiedad hacia esta disciplina (Ávila-Toscano, Rojas-Sandoval y Tovar-Ortega, 2020).
Lo indicado se puede resumir, con base en Hannula (2016), en que si bien se suele considerar la matemática como la disciplina académica más lógica y objetiva, se reconoce ampliamente “que el pensamiento matemático no es un razonamiento puramente lógico, sino que está influenciado en gran medida por características afectivas” (p. 32). La valoración e incorporación de los elementos afectivos ha dado lugar a la conceptualización del llamado “dominio afectivo” que, de acuerdo con McLeod (1989), se puede concebir como “un extenso rango de estados de ánimo que son generalmente tomados como algo diferente de la pura cognición, e incluye como componentes específicos las creencias, las actitudes y las emociones” (p. 245).
No existe consenso sobre los elementos constituyentes del dominio afectivo. McLeod (1992 y 1994) identificó tres conceptos básicos: las creencias, las actitudes y las emociones. DeBellis y Goldin (1999) amplían el modelo de McLeod al sugerir que se incluya un cuarto subdominio que trata de valores, la ética y la moral; este se encuentra conectado con los otros tres subdominios. En posiciones más recientes, Grootenboer y Marshman (2015) proponen que en el tema del afecto en educación matemática se consideren las creencias, los valores, las actitudes y las emociones; por su parte, Hannula (2016) plantea que, además de las actitudes y las creencias, se incorporen los valores, las motivaciones, las normas sociales y la identidad.
Dentro del dominio afectivo, las actitudes, entendidas como “aquellas que expresan algún grado de aprobación o desaprobación, gusto o disgusto, acercamiento o alejamiento” (Mato, 2006, p. 40), han generado gran interés en las últimas décadas, porque diversos estudios han encontrado que son un factor clave a la hora de comprender y explicar la variabilidad de resultados e los estudiantes en matemáticas (Román, Mera, Aragón y Delgado, 2019).
Dos de las variables más estudiadas del dominio afectivo son la “ansiedad matemática” y la “autoconfianza matemática”. Se ha determinado relación inversa entre estas variables, en el sentido de que el estudiantado con más ansiedad presenta menor confianza en sus habilidades matemáticas (Pérez-Tyteca y Castro, 2011; Morales y Arce, 2017; Wynta y López, 2017). Diversos estudios, a lo largo del tiempo, han encontrado diferencias en el nivel de autoconfianza matemática según el sexo del estudiantado: en la mayoría de los casos, las mujeres manifiestan niveles menores (Sherman, 1983;Reyes, 1984; McLeod, 1992; Ramos, 2015; Calderón y Guillén, 2016; Arrieta, 2016; Sánchez y Jiménez, 2016; Meza, Agüero y Suárez, 2019, Morales y Arce, 2017; Vega, 2017; Coto, 2018 y Báez y Meza, 2020, aunque no en todos (Wynta y López, 2017).
También se han detectado diferencias en el nivel de ansiedad matemática según el sexo, con niveles mayores para las mujeres (Mena, 2014; Meza, Agüero, Suárez y Schmidt, 2014); Corrales, 2014; Castillo y Picado, 2014; Ramos, 2015; Arrieta, 2016; Calderón y Guillén, 2016; Morales y Arce, 2017; Wynta y López, 2017; Vega, 2017; Blanco, 2019; Báez y Meza, 2020; Delgado, Castro y Pérez-Tyteca, 2020; y Solano, Garro y Meza, 2021), aunque algunas investigaciones no han encontrado diferencias (Carroll, 2010; Tapia y Marsh, 2004) o que el mayor nivel de ansiedad se ha manifestado en los hombres (Husni, 2006: De la Torre, Mato y Rodríguez, 2009). Por su parte, algunas investigaciones han encontrado que las mujeres afrontan la ansiedad matemática mejor que los hombres (Hannula, 2016). La correlación lineal positiva entre el rendimiento académico y el nivel de autoconfianza matemática ha sido detectada en algunos estudios, lo cual significa que altos niveles de autoconfianza matemática están asociados a mejor rendimiento académico (Pérez-Tyteca, 2012 y Arrieta, 2016). De igual manera, algunos estudios han evidenciado que a mayor nivel de ansiedad matemática hay rendimientos académicos bajos y el evitar cursos relacionados con la matemática (Pérez-Tyteca, 2012).
En otras variables del dominio afectivo en matemática, como la “actitud hacia la utilidad de la matemática”, también se han encontrado diferencias entre hombres y mujeres, con niveles menores para ellas (Camacho y Picado, 2015; Campos y Mora, 2015; Meza, Suárez y Agüero, 2015; Morales y Arce, 2017; Muñoz y Meza, 2019; Coto, 2018; y Báez y Meza, 2020).
No obstante la cantidad de investigaciones que detectan diferencias entre hombres y mujeres en el nivel de diversas variables del dominio afectivo en matemática, no se han establecido relaciones causales para explicarlas. Para Fennema (1996) ), las discrepancias se pueden deber a factores como el estatus económico, la escuela, el profesorado o la etnicidad; es decir, las diferencias entre hombres y mujeres podrían explicarse por el contexto sociocultural y económico. Una posición similar sostiene Gamboa (2012), quien considera que las diferencias podrían deberse a estereotipos sociales, como que los hombres son buenos en matemática y las mujeres son deficientes, o a que tales estereotipos inhiben a las mujeres a participar en tantas actividades educativas relacionadas con la matemática como lo hacen los hombres.
Otra posibilidad explicativa de las diferencias entre hombres y mujeres en las variables de dominio afectivo, y generalmente con resultados menos favorables para estas últimas, la plantean Monje y Pérez-Tyteca (2020), quienes sugieren que las diferencias podrían no ser reales, sino que se deberían al hecho de que las mujeres suelen responder los instrumentos con mayor sinceridad. Otra línea de investigación que ha recibido atención en el dominio afectivo en educación matemática es la influencia del ambiente familiar. Una investigación de Farr (2015) sugiere que tipos indirectos de involucramiento de los padres y madres, como sus actitudes hacia la matemática, pueden ser más influyentes en la actitud de los niños hacia la matemática que los tipos directos de participación como el acompañamiento en la resolución de tareas. (p. 251).
Cervantes, Arenas y Aroca (2015) encontraron que la actitud hacia la matemática de los padres y madres afecta el proceso de formación de sus hijos en matemática. Por su parte, Knap, Landers y Liang (2016) señalan que tales actitudes y la confianza para aprender la disciplina impactan el rendimiento académico del estudiantado en matemática, y Mohr-Schroeder et al (2017) hallaron que “la actitud de los padres y madres funge como un factor de predicción relevante de la actitud de sus hijos hacia la matemática” (p. 220).
Entre las variables del dominio afectivo que han comenzado a llamar la atención de los grupos de investigación, se encuentra la predisposición desfavorable hacia el aprendizaje de la matemática, entendida como “la percepción desfavorable hacia el enfrentamiento o abordaje de tareas en el ámbito matemático. Esta se expresa como disgusto, desagrado, falta de perseverancia o desinterés hacia las tareas matemáticas” (Cerda, Pérez, Aguilar y Aragón, 2018). La predisposición desfavorable hacia el aprendizaje de la matemática tiene relación con las “creencias del estudiantado sobre sus expectativas de éxito o su percepción de autoeficacia” (Cerda, Ortega, Casas, Del Rey y Pérez, 2016).
La importancia de esta variable la resaltan Cerda y Pérez (2015, p. 191) al indicar que la “disposición o motivación con la cual los estudiantes se enfrentan a las asignaturas de su entorno escolar, sobre todo en matemáticas, puede considerarse una variable relevante para el aprendizaje”. Esto se confirma con el planteamiento de Hannula (2016, p. 33) de que la “tendencia general es que un estudiante que tiene disposición positiva hacia las matemáticas tiende a experimentar emociones positivas con mayor frecuencia y emociones negativas con menor frecuencia que un estudiante con disposición negativa”.
Los resultados de algunas investigaciones sugieren que la variable predisposición desfavorable hacia el aprendizaje de la matemática permite aproximaciones explicativas sobre el éxito o fracaso en el proceso de aprendizaje de la matemática (Cerda et al., 2016). Asimismo, se ha constatado una correlación negativa entre la predisposición desfavorable hacia el aprendizaje y el rendimiento académico en matemática (Cerda y Pérez, 2015).
La variable también ha resultado relevante en su capacidad explicativa de la variabilidad de los rendimientos académicos, tanto generales como particulares en matemática, en interacción con variables como “la inteligencia lógica, los esquemas de razonamiento formal, como también con el nivel de competencias matemáticas tempranas y factores de convivencia escolar” (Cerda, Romera, Casas, Pérez y Ortega-Ruiz, 2017).
La búsqueda de estudios similares llevados a cabo en Costa Rica, en bases de datos (Scopus, Web of Science, Redalyc, Scielo, EBSCO y Dialnet), en repositorios institucionales (Kimuk, RepositorioTEC), metabuscadores (BASE y OpenDoar) y catálogos de universidades costarricenses (Universidad de Costa Rica, Instituto Tecnológico de Costa Rica, Universidad Nacional y Universidad Estatal a Distancia), con los términos “Negative Predisposition towards Mathematics” y “Unfavorable predisposition towards mathematics learning”, y Costa Rica, así como en su versión en español, arrojó solo dos resultados: tanto la investigación de Solano, Garro y Meza (2021) como la de Martínez y Ramírez (2022), ambas vinculadas al grupo que desarrolló la investigación que se reporta en este artículo, por lo que se puede considerar que los dos estudios detectados, y el que se presenta en este trabajo, son pioneros en la temática en Costa Rica.
Método
Este estudio tiene carácter descriptivo-exploratorio, desde un enfoque cuantitativo. En esta sección se presentan las características de la muestra, información sobre el instrumento de medición aplicado, el procedimiento para recabar los datos y la descripción de las técnicas estadísticas empleadas.
Participantes
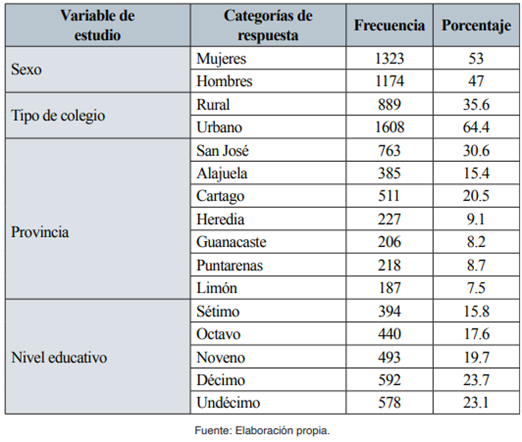
La muestra de la investigación estuvo conformada por 2497 estudiantes de colegios oficiales diurnos de la República de Costa Rica (53% de mujeres). Se efectuó un muestreo simple aleatorio estratificado para seleccionar a los colegios participantes a partir de un listado oficial de instituciones de educación media diurnas, según la zona de ubicación (rural o urbana) y provincia, con base en la cantidad de estudiantes de cada provincia y tipo de colegio. El instrumento de medición se aplicó al estudiantado de la primera sección de cada nivel. La distribución final de la muestra se presenta en la Tabla 1.
Variables
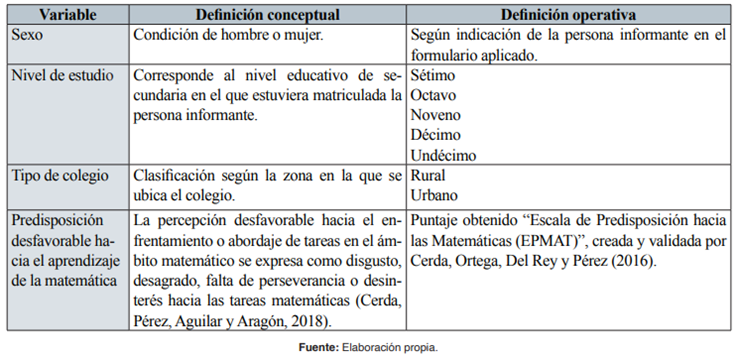
Las variables consideradas en el estudio, más su definición conceptual y operativa se presentan en la Tabla 2.
Instrumento de medición
La predisposición desfavorable hacia el aprendizaje de la matemática fue medida aplicando el instrumento denominado “Escala de Predisposición hacia las Matemáticas (EPMAT)”, creado y validado por Cerda, Ortega, Del Rey y Pérez (2016). Se trata de una escala tipo Likert, integrada por 6 reactivos con cinco opciones de respuesta, desde “totalmente de acuerdo” a “totalmente en desacuerdo”, y que mostró un valor de alfa de Cronbach de 0.82 en el estudio original (Cerda et al, 2016).
Para estudiar la validez del instrumento, se calculó el índice de discriminación de cada ítem. Para esto, se recurrió al cómputo de la correlación entre la puntuación aportada por el ítem y la obtenida por la suma de los otros ítems (restando el ítem evaluado) e interpretando su valor según la baremación sugerida en Lozano y De La Fuente-Solana (2013). Todos los ítems superaron el valor mínimo de 0.3, recomendado como valor mínimo aceptable (Lozano y De La Fuente-Solana, 2013).
Se estudió, además, la razonabilidad de asumir el supuesto de unidimensionalidad de la escala mediante la técnica del análisis factorial, por ser la más utilizada para tal efecto (Jiménez y Montero, 2013) para evidenciar que mide esencialmente un solo constructo, previo cálculo del índice de adecuación muestral de Kaiser-Meyer y Olkin (KMO), con un valor de 0.884 y de esfericidad de Bartlett (p = 0 < 0.05). Como criterio de unidimensionalidad, se recurrió al recomendado en Carmines y Zeller (1979, citado en Burga (2006), el cual exige que el primer factor explique al menos el 40 % de la varianza total (60 % para este estudio). La confiabilidad (o fiabilidad de la escala) se estudió con la técnica alfa de Cronbach, con un valor de 0.864; esto significa, de acuerdo con Cea (1999), que posee una confiabilidad adecuada.
Procedimineto
El instrumento se aplicó al estudiantado de las secciones previstas de los colegios seleccionados en línea, salvo en unos grupos de la provincia de Limón y de Guanacaste donde hubo que recurrir a formularios impresos dada la baja respuesta obtenida. Para concretar la recolecta de datos, se hizo llegar información a la persona docente contacto de cada colegio y se le indicó el enlace de la aplicación que debía utilizar.
Análisis estadístico
El análisis estadístico descriptivo de los datos contempla la baremación de los puntajes en las categorías baja y alta, según el puntaje sea inferior o superior, respectivamente, al valor medio de la escala. Además, con el propósito de inferir resultados, se contrastaron las siguientes hipótesis:
Hipótesis 1: No existen diferencias en el nivel de predisposición desfavorable hacia el aprendizaje de la matemática, según el sexo.
Hipótesis 2: No existen diferencias en el nivel de predisposición desfavorable hacia el aprendizaje de la matemática, según el nivel educativo.
Hipótesis 3: No existen diferencias en el nivel de predisposición desfavorable hacia el aprendizaje de la matemática, según el tipo de colegio.
Para la primera y la tercera hipótesis, se aplica la prueba paramétrica t de Student, se asume la normalidad de la distribución de los datos, con base en el teorema del límite central, al considerar que cada una de las categorías tiene más de 100 elementos. Para la segunda hipótesis se aplica la prueba ANOVA, dado que la prueba de Levene detectó homogeneidad de varianzas, complementada con la prueba a posteriori de Scheffé.
Para los casos en que se detectan diferencias estadísticamente significativas, se calcula el tamaño del efecto empleando la d de Cohen (Morales-Vallejo, 2012), que estima el número de desviaciones típicas que separan a dos grupos. Para interpretar la magnitud de los tamaños del efecto medidos por la d de Cohen, se recurre a las referencias establecidas por Cohen (Morales-Vallejo, 2012): en torno a 0.20 (diferencia pequeña), 0.50 (diferencia moderada) y 0.80 o más (diferencia grande).
Resultados
Clasificación del nivel de predisposición desfavorable hacia el aprendizaje de la matemática
El nivel medio de predisposición desfavorable hacia el aprendizaje de la matemática (M = 15.62, DT = 5.91) fue significativamente menor que el promedio de la escala (t (2496) = -15.88, p = 0 < 0.05). Esto indica que, globalmente, el estudiantado de la muestra manifiesta un nivel de “Predisposición desfavorable hacia el aprendizaje de la matemática” inferior al promedio.
La clasificación de los puntajes obtenidos para determinar la predisposición desfavorable hacia el aprendizaje de la matemática indica 70% para la categoría baja y 30% para la alta.
Contraste de la hipótesis 1
Para el contraste de la primera hipótesis, se comparó la media de los hombres (M = 14.8, DT = 5.96) con la media de las mujeres (M = 16.32, DT = 5.75) y se encontró una diferencia estadísticamente significativa (t (2458) = -6.44, p = 0.25). Se desprende que se rechaza la hipótesis nula y se acoge la alternativa, lo cual indica que existen diferencias en el nivel de predisposición desfavorable hacia el aprendizaje de la matemática, con media más baja para los hombres y un tamaño del efecto (d = 0.25) interpretable como una diferencia pequeña.
Contraste de la hipótesis 2
Para el estudio de la segunda hipótesis, se comparó la media de los cinco niveles educativos, se utilizó la prueba ANOVA. La prueba de Levene (p = 0.732 > 0.05) indica que se puede asumir la hipótesis de igualdad de varianzas y se determinó que existen diferencias estadísticamente significativas entre al menos un par de medias de los cinco niveles (F (4,2492) = 4.027, p = 0.03 < 0.05).
Se utilizó la prueba post hoc de Scheffé, para comparar los diferentes pares de medias y se encontró que la del estudiantado de sétimo (M7 = 14.94, DT7 = 5.71, p < 0.05) es significativamente menor que la de décimo (M10 = 16.36, DT10 = 5.87, p < 0.05), con un tamaño del efecto bajo (d=0,244).
En otros términos, existen diferencias estadísticamente significativas en el nivel de predisposición desfavorable hacia el aprendizaje de la matemática entre el estudiantado del sétimo en comparación con el de décimo.
Contraste de la hipótesis 3
Para analizar la tercera hipótesis, se comparó la media de los colegios urbanos (M = 15.37, DT = 5.95) con la media de los colegios rurales (M = 16.06, DT = 5.81) y se encontró una diferencia estadísticamente significativa (t (2458) = -2.814, p = 00.05, d=0.25). Se desprende que se rechaza la hipótesis nula y se acoge la alternativa. Esto indica que existen diferencias en el nivel de predisposición desfavorable hacia la matemática, con media más baja para los colegios urbanos y un tamaño del efecto (d = 0.11) interpretable como bajo.
Discusión
En este estudio se analizó la predisposición desfavorable hacia la matemática del estudiantado de colegios académicos diurnos costarricenses matriculados en el año 2022. Los resultados indican que, aproximadamente, un 70% estudiantado participante en la investigación manifiesta niveles bajos de predisposición desfavorable hacia la matemática. Esto se valora como un hallazgo positivo y se confirma con el hecho de que el valor medio de la variable en la muestra es significativamente menor que la media de la escala.
Este hallazgo resulta alentador, pues no solo existe evidencia de que la matemática suele ser percibida por sectores importantes del estudiantado como una materia difícil, aburrida, poco práctica, abstracta, etc., cuyo aprendizaje requiere una capacidad especial y no siempre al alcance de todos (Gil et al., 2006; Meza y Azofeifa, 2011), sino que ocurre en un periodo temporal en el que Costa Rica enfrenta un “apagón educativo”, en el cual se señala que el país vive la peor crisis de las últimas décadas en materia educativa (Octavo Informe Estado de la Educación, 2021). Desde una perspectiva práctica, el hallazgo sugiere que en los esfuerzos por mejorar el aprendizaje de la matemática en la educación media, los que deben ser asumidos con prontitud ante el panorama evidenciado en el Octavo Informe Estado de la Educación (2021), pueden asumirse posiciones optimistas de éxito porque la “disposición o motivación con la cual los estudiantes se enfrentan a las asignaturas de su entorno escolar, sobre todo en matemáticas, puede considerarse una variable relevante para el aprendizaje” (Cerda y Pérez, 2015, p. 191).
Además, niveles bajos de predisposición desfavorable hacia el aprendizaje de la matemática como los encontrados en la investigación avizoran posibilidades positivas de mejoramiento de la calidad de la educación matemática en Costa Rica. Esto por cuanto se ha constatado una correlación negativa entre la predisposición desfavorable hacia la matemática y el rendimiento académico en esta materia (Cerda y Pérez, 2015).
No obstante, la lectura positiva del hallazgo debe ser cautelosa, por cuanto no se puede dejar de lado que un 30% del estudiantado mostró niveles altos de predisposición desfavorable hacia la matemática. Este elemento podría incidir negativamente en el logro de las acciones encaminadas al mejoramiento de los procesos de enseñanza y de aprendizaje de la matemática que se emprendan en Costa Rica en los próximos años y que pudiera ser considerado en las acciones de intervención educativa. Las diferencias en el nivel de predisposición desfavorable hacia la matemática entre hombres y mujeres, con niveles más altos para las mujeres, no concuerdan con los obtenidos por Solano et al. (2021) en los que las mujeres mostraron niveles más bajos que los hombres. No obstante, sí lo hacen con los obtenidos por Martínez y Ramírez (2022). Esto contribuye a pensar que las diferencias presentes en algunas investigaciones pueden deberse efectivamente a influencias culturales y no a razones de capacidad intelectual de alguno de los dos sexos para hacer o aprender matemática.
También concuerdan con los hallazgos de otras investigaciones realizadas en Costa Rica en el dominio afectivo en el campo de la matemática, en los que las mujeres han mostrado resultados menos favorables (Meza et al., 2015; Agüero et al., 2016; Agüero Meza, Suárez y Schmidt, 2017; Delgado, Espinoza y Fonseca, 2017; y Meza, Agüero y Suárez,, 2019), aunque al resultar el “tamaño del efecto” bajo no parecen ser necesarias actividades de intervención educativa tendientes a mejorar el nivel de la variable haciendo diferencias por sexo.
La investigación, por su carácter descriptivo, no aporta información sobre las causas que puedan explicar las diferencias en el nivel de la variable por sexo y podría deberse, tal como han señalado Fennema (1996) o Gamboa (2012), a patrones culturales presentes en la sociedad costarricense, o, como han sugerido Monje y PérezTyteca (2020), podrían deberse a que las mujeres estén más dispuestas a responder de manera más sincera que los hombres en estas temáticas.
Las diferencias detectadas entre estudiantes de sétimo y décimo, con niveles menos favorables para décimo, concuerdan para el ámbito costarricense con los reportados en Agüero et al. (2017) para la ansiedad matemática y en Meza et al.(2019) para la autoconfianza matemática, en los que los niveles iniciales de la educación media muestran mejores resultados que en los últimos. Esta situación, como se ha señalado, resulta preocupante de cara a la escogencia de carrera universitaria por cursar (Pérez-Tyteca, 2012).
Finalmente, las diferencias encontradas en el nivel de predisposición desfavorable hacia el aprendizaje de la matemática entre el estudiantado de los colegios urbanos en comparación con los de los colegios rurales, al presentar un “tamaño del efecto” sumamente bajo, aunado a que en Meza et al. (2019) no se encontraron diferencias para la variable autoconfianza matemática, no parecen justificar el desarrollo de acciones de intervención educativa tendientes a mejorar el nivel de esa variable que considere la zona donde se ubica la institución educativa.
Los hallazgos de la investigación sugieren la conveniencia del desarrollo de estudios similares en otros ámbitos educativos, como la educación primaria o la educación superior o que contemplen instituciones de educación secundaria oficiales nocturnas o pertenecientes a la educación privada que no fueron parte de la investigación.
Conclusiones
La investigación permite llegar a las siguientes conclusiones:
El nivel medio de predisposición desfavorable hacia el aprendizaje de la matemática fue significativamente menor que el promedio de la escala, esto indica que globalmente el estudiantado de la muestra presenta un nivel en esa variable inferior al promedio; es decir, manifiestan en general una predisposición desfavorable hacia la matemática baja.
La clasificación de los puntajes obtenidos para la predisposición desfavorable hacia la matemática indica un 70% para la categoría baja y un 30% para la categoría alta.
Se encontraron diferencias en el nivel de predisposición desfavorable hacia el aprendizaje de la matemática entre hombres y mujeres, con media inferior para los hombres y con un tamaño del efecto que se interpreta como diferencia pequeña.
Se detectaron diferencias estadísticamente significativas en el nivel de predisposición desfavorable hacia el aprendizaje de la matemática entre el estudiantado de sétimo y décimo nivel, con mayor valor medio para décimo y tamaño del efecto pequeño.
Se hallaron diferencias en el nivel de predisposición desfavorable hacia el aprendizaje de la matemática por tipo de zona donde se ubica el colegio, con niveles superiores en promedio para el estudiantado de los colegios rurales.
Agradecimientos
Trabajo desarrollado en el marco del proyecto de investigación “PREDAM: Predisposición desfavorable hacia la matemática en la educación media costarricense”, bajo el código 5402-1490-2401. Se agradece el apoyo de la Vicerrectoría de Investigación y Extensión del Instituto Tecnológico de Costa Rica.
Declaración de la contribución de los autores
El porcentaje total de contribución para la conceptualización, preparación y corrección de este artículo fue el siguiente: L. G. M. 20 %, Z. S. V-A. 20 %, E. A. C. 20 %, R. J. C. 10 %, M. C. F. 10 %, L. S. M. 10 %, P. P-T. 5 %, J. M. P. 5 %.